Економічні науки/4. Математичні методи в економіці

Студентка, Шаргородська Вікторія Борисівна

Вінницький торговельно-економічний інститут КНТЕУ,Україна.

Математична модель управління інвестиційними процесами

Перехід до ринкових умов господарювання зумовив докорінні зміни у всіх сферах економічної діяльності в Україні. Починаючи з 1991 року українські підприємства були змушені переходити на нові принципи діяльності, що в свою чергу призвело до появи багатьох проблем і зумовило необхідність теоретичного аналізу базових категорії ринкових відносин, без яких неможливе створення та функціонування адекватних ринкових механізмів, до яких належить і механізм здійснення інвестиційної діяльності[2,37]. Інвестиції є важливим фактором економічного розвитку, а інвестиційна політика підприємств - центральною ланкою загальнодержавної економічної політики. Сучасна наука розробила досить різноманітний економіко-математичний інструментарій оптимізації інвестиційної діяльності підприємств. У досліджені цих проблем вагомим є внесок вітчизняних вчених А.А. Алексєєва, В.В. Вітлінського, В.М. Вовка, В.В. Гнатушенка, В.М. Порохні та ін., а також зарубіжних вчених Є.Ф. Брігхема, С.В. Валдайцева, Дж. Ван Хорна, М.В. Грачової та ін.[1,78].

Основною метою статті є аналіз і розвиток теоретичних, методологічних підходів та побудова адекватної моделі управління інвестиційною діяльністю підприємства. Для досягнення цієї мети були послідовно поставлені та розв’язані такі основні завдання:

- дослідити особливості здійснення інвестиційної діяльності підприємствами в умовах невизначеності;

- обґрунтувати поетапність планування інвестиційної діяльності;

- проаналізувати вітчизняну та міжнародну практику оцінки ефективності реальних інвестицій та оптимізації процесу інвестування;

- сформулювати в аналітичному вигляді задачі формування ефективного інвестиційного портфеля підприємства;

- розробити модель формування ефективного інвестиційного портфеля підприємства, що враховує зміни ефективності реалізації проектів у часі та їх технологічно можливий поділ на частини;

- розробити модель розподілу у часі реалізації проектів інвестиційного портфеля підприємства;

- розробити модель узгодження фінансово-інвестиційної програми підприємства;

- провести числову апробацію побудованих моделей ефективного планування інвестиційної діяльності[3,68].

Практичне значення статті полягає у розробленні економіко-математичного інструментарію та практичних рекомендацій, які можуть бути використані на підприємствах для прийняття інвестиційних рішень.

У процесі аналізу інвестиційних альтернатив одним із найбільш важливих питань є визначення оптимального варіанту фінансування проекту. Для його знаходження використаю наступну модель. Припустимо, що підприємство має можливість профінансувати реалізацію інвестиційного проекту m способами. Для кожного виду фінансування j розраховують відповідну ставку дисконтування, яка дорівнює середньозваженій вартості капіталу при j-му варіанті фінансування r_j^WACC . Оскільки зміна варіантів фінансування може призводити до зміни періоду впровадження проекту, то порівняння альтернатив слід здійснювати з допомогою показника чистої теперішньої вартості. Оптимальним є варіант, що максимізує NPV проекту, а модель його вибору має наступний вигляд:

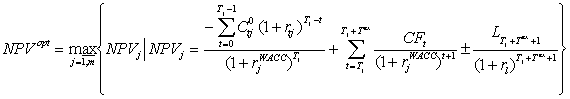, (1) де NPV_j – чиста теперішня вартість проекту при j–му варіанті фінансування; T_j – тривалість впровадження проекту при j – му варіанті фінансування; C_jt⁰ - обсяг капіталу, вкладеного у періоді t, згідно j–го варіанту фінансування; r_tj – вартість капіталу, вкладеного у період t, згідно j–го варіанту фінансування; T^ex – тривалість експлуатації проекту.

Отже, такий аналіз ефективності інвестиційних альтернатив дозволить інвестору в повному обсязі врахувати інвестиційні витрати, отримати адекватне значення NPV проекту та обрати найбільш ефективний варіант фінансування.

Література:

1. Богатов О. И., Лысенко Ю. Г., Петренко В. Л., Скобелев В. Г. Рейтинговое управление экономическими системами. – Донецк: Юго-Восток, 1999. – 110 с.

2. Козаченко Г.В., Антіпов О.М., Ляшенко О.М., Дібніс Ґ.І. Управління інвестиціями на підприємстві. - К.: Лібра, 2004. - 368 с.

3. Романюк Т. П., Терещенко Т. О., Присенко Г. В., Городкова І. М. Математичне програмування: Навч. посіб. – К.: ІЗМН, 1996. – 312 с.