К

К.т.н. Рвачева Н.В., Кривошапка К.В.

Полтавский национальный технический университет

имени Юрия Кондратюка

Моделирование интенсивности трафика реального времени в канале телекоммуникационной сети с коммутацией пакетов

В современных телекоммуникационных сетях с коммутацией пакетов (ТСКП) при передаче речевых сообщений и потоки видеоинформации образуется мультимедийный трафик. Интенсивность передачи информации, инициированной работой в реальном времени какого-либо мультимедийного приложения, достаточно высока и близка к постоянному значению, поэтому такой вид трафика часто именуют потоковым трафиком или трафиком реального времени [1 – 3]. Для качественной передачи потокового трафика необходимо минимизировать задержку пакетов и ее дисперсию (джиттер), что возможно при осуществлении эффективного управления потоками реального времени в условиях наличия ограниченных сетевых ресурсов [4]. В процессе разработки методов управления потоками реального времени в ТСКП целесообразно использовать математические модели, имитирующие процесс динамического изменения интенсивности трафика реального времени в канале ТСКП.

Поэтому актуальной является задача, состоящая в разработке методики создания адекватных моделей, имитирующих изменение во времени величины интенсивности трафика реального времени в канале телекоммуникационной сети с коммутацией пакетов.

Для моделирования передаваемых по каналу потоков реального времени необходимо обосновать законы распределения и характеристики случайных величин (интервала времени между моментами начала передачи по этому каналу потоков реального времени) и (длительности передачи по этому каналу потоков реального времени). В рамках теории массового обслуживания предложены модели, адекватно описывающие функционирование узла коммутации телефонных каналов, на который поступает поток запросов на установление соединение [5 – 7]. Наиболее распространенные модели поступления в такую систему вызовов и их обслуживания, предполагают, что плотность распределения интервала времени между поступлением вызовов, а также плотность распределения длительности их обслуживания подчиняются экспоненциальному закону. Обоснованным представляется допущение о том, что плотность распределения временного интервала между моментами начала передачи потоков реального времени, а также плотность распределения длительности их передачи соответствуют экспоненциальному закону.

Постановка задачи

Заданы:

1) величина – пропускная способность канала, по которому требуется передавать потоки реального времени;

2) множество потоков реального времени , где – номер потока, который требуется передавать по каналу;

3) множество , где – требуемое значение интенсивности передачи потока ;

4) множество , где – значение момента времени, соответствующего началу передачи потока ;

5) интервал времени моделирования .

Необходимо: определить значения интенсивности трафика реального времени в канале ТСКП в каждый текущий момент времени .

Допущения:

1) интервал времени между соседними моментами начала передачи потоков реального времени по каналу является случайной величиной , которая распределена по экспоненциальному закону и характеризуется математическим ожиданием ;

2) длительность передачи потока реального времени по каналу является случайной величиной , характеризующейся экспоненциальным законом распределения и математическим ожиданием .

Задача получения значений, которые принимает в текущий момент времени величина интенсивности трафика реального времени в канале ТСКП, сводится к определению величины – суммарной интенсивности потоков реального времени, передаваемых по рассматриваемому каналу в данный момент времени.

При определении величины необходимо учитывать, что суммарная интенсивность одновременно передаваемых по одному и тому же каналу потоков не может превышать пропускную способность этого канала. Передача потока в момент времени возможна лишь при выполнении условия:

, (1)

где – значение суммарной интенсивности потоков реального времени, которые требуется передавать по каналу ТСКП в момент времени .

Значение определяется из выражения:

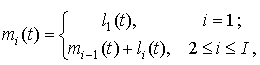, (2)

где – требуемое значение интенсивности передачи потока в момент времени .

Определив по формуле (2) множество , можно найти искомую величину как удовлетворяющее условию (1) наибольшее значение суммарной интенсивности потоков реального времени, которые требуется передавать по каналу ТСКП в момент времени :

В формуле (2) неизвестными являются значения . Если в момент времени требуется передавать поток , то требуемое значение интенсивности его передачи в этот момент времени будет соответствовать заданному значению , в противном случае – будет нулевой:

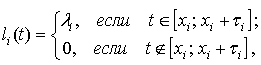(3)

где – значение момента времени, когда требуется начать передачу потока ; – требуемое значение длительности передачи потока .

Согласно сделанных допущений, известно, что случайная величина распределена по экспоненциальному закону. Поэтому плотность распределения требуемой длительности передачи потока из множества может быть представлена в виде функции:

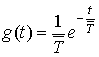Для получения значений какой-либо случайной величины в процессе моделирования используют специальные датчики, которые, как правило, генерируют значения случайной величины, имеющей равномерное распределение в интервале (0, 1). В реальности такие датчики генерируют не случайные, а достаточно близкие к ним псевдослучайные числа. Имея последовательность равномерно распределенных случайных чисел , , можно вычислить значения случайных чисел с экспоненциальным распределением и средним значением по формуле [8]:

Поэтому, используя датчик, генерирующий равномерно распределенные значения случайных чисел , можно получить значения случайной величины :

. (4)

В формуле (3) неизвестным является множество значений . Элементы этого множества можно последовательно найти, используя выражение:

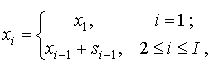(5)

где – величина интервала между моментами времени и .

В качестве примера на рис. 1 иллюстрируются моменты начала передачи потоков реального времени, интервалы между ними и значения длительности передачи этих потоков по каналу ТСКП.

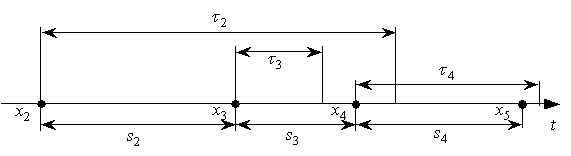
Рис. 1. Моменты начала передачи потоков реального времени, интервалы между ними и значения длительности передачи этих потоков по каналу сети

Для решения поставленной задачи остается получить множество значений . Известно, что плотность распределения случайной величины , соответствующая экспоненциальному закону, имеет вид:

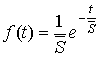Поэтому для определения значений случайной величины можно воспользоваться выражением:

. (6)

Методика моделирования интенсивности трафика реального времени в канале ТСКП, блок-схема алгоритма реализации которой представлена на рис. 2.

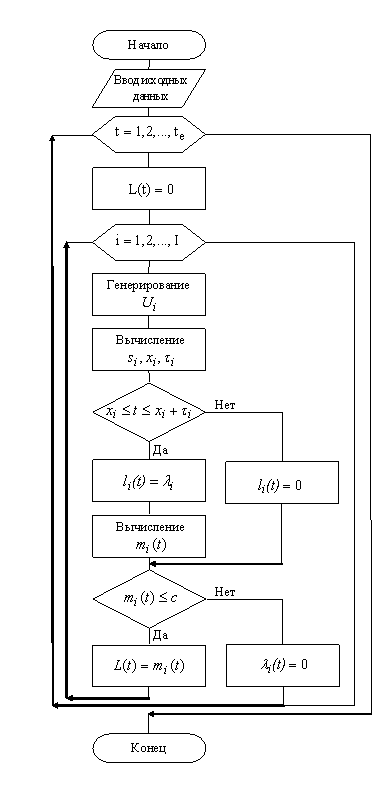
Рис. 2. Блок-схема алгоритма, реализующего методику моделирования интенсивности трафика реального времени в канале ТСКП

Таким образом, в статье предложена методика моделирования интенсивности трафика реального времени в канале ТСКП, которая основана на экспоненциальном распределении моментов начала передачи и длительности передачи потоков реального времени.

Применение указанной методики позволяет создавать адекватные модели, имитирующие процесс динамического изменения интенсивности трафика реального времени в канале ТСКП.

Литература

1. Кучерявый Е.А. Управление трафиком и качество обслуживания в сети Интернет. – СПб.: Наука и техника, 2004. – 336 с.

2. Куроуз Дж., Росс К. Компьютерные сети. 2-е изд. – СПб.: Питер, 2004. – 765 с.

3. Столлингс В. Современные компьютерные сети. 2-е изд. – СПб.: Питер, 2003. – 783 с.

4. Вегенша Ш. Качество обслуживания в сетях IP: Пер. с англ. – М.: Издательский дом «Вильямс», 2003. – 386 с.

5. Вишневский В.М. Теоретические основы проектирования компьютерных систем. – М.: Техносфера, 2003. – 512 с.

6. Математичні основи теорії телекомунікаційних систем / В.В. Поповський, С.О. Сабурова, В.Ф. Олійник, Ю.І. Лосєв, Д.В. Агеєв та ін.: За ред. В.В. Поповського. – Харків: ТОВ «Компанія СМІТ», – 2006. – 564 с.

7. Шварц М. Сети связи: протоколы, моделирование и анализ. Ч.1: Пер. с англ. – М.: Наука, 1992. – 336 с.

8. Крылов В.В., Самохвалова С.С. Теория телетрафика и ее приложения. – СПб.: БХВ-Петербург, 2005. – 288 с.