Трояновська Т. І.

Україна, Вінницький технічний коледж

Формалізація адаптивного курсу підготовки в СКП спеціалістів

Анотація

У даній статті розглядається питання формалізації адаптивного курсу підготовки (АКП) для системи комп’ютеризованої підготовки (СКП) спеціалістів з точки зору фреймоового представлення даних.

Вступ

З метою дозволити суб¢єкта підготовки можливість отримувати кваліфікації за допомогою СКП спеціалістів, Г. Вебер [1], пропонує додати певну адаптивність, яка «пристосовує» роботу з адаптивним курсом підготовки (АКП) під особливості вибору чи особливості діяльності окремого суб¢єкта підготовки [2].

Постановка мети. Для того, щоб обґрунтувати та показати спосіб досягнення адаптивності, необхідно визначити основні поняття, компонети АКП та залежності між ними. Для математичного опису було обрано теорію множин, матричне числення, теорію функцій та логіку предикатів.

Основний виклад матеріалу

Ядром СКП що розробляється, є сховище знань. Припустимо, що для загального випадку таке сховище складається з теоретичних та практичних елементів. Теоретичним елементом вважається чисто інформативний (описовий) фрагмент навчального матеріалу (НМ), який визначає, пояснює або описує важливі аспекти даного поняття, явища або процесу. Практичним елементом вважається фрагмент НМ, який містить наочне пояснення, вправу, або інший інтерактивний засіб, що дозволяє суб¢єкту підготовки скласти враження про описуване поняття, явище чи процес. Тест також вважатимемо практичним елементом.

Отож, узагальнену формалізовану модель сховища знань для СКП спеціалістів з точки зору складових можна записати виразом (1):

, (1)

де - функція формування СКП спеціалістів; – множина теоретичних елементів, що входять у дану СКП спеціалістів, і є її статичною частиною; – множина практичних елементів, і є динамічною частиною системи. Приймемо, що – числове значення потужності та запишемо функцію у вигляді динамічної матриці:

,

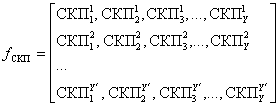де - кількість можливих перестановок . В даній матриці кожен рядок є множина, яка розглядається як вектор. Вектор цей, в свою чергу, є одним із варіантів перестановок загальної множини СКП, таким чином, функція є функцією вибірки одного (або декількох) варіантів перестановок.

Приймемо, що теоретичні та практичні елементи АКП складаються з логічно завершених пакетів (порцій) інформації, які містять мінімально необхідний набір теоретичних та/або практичних елементів, що дають можливість опанувати конкретне явище чи процес – тобто, фреймів [3].

Фрейм (F) можна визначити як множину:

Гіпертекстові технології дозволяють включити у фрейм елементи, які не належать даній СКП спеціалістів. Відповідно до цієї можливості, можна виокремити гомогенні та гетерогенні фрейми.

Гомогенним вважатимемо фрейм, всі елементи якого входять до даної СКП спеціалістів. Гетерогенним вважатимемо фрейм, до складу яких також входять елементи інших систем. Для того, щоб дати формальне математичне визначення, сформулюємо вирази для відповідних підмножин:

;	(2)
;	(3)
;	(4)
.	(5)

Вирази (2) та (3) позначають елементи, які належать даній СКП, а останні – (4) та (5) – ті, які не є складовою частиною системи. В рамках даної роботи останні два вирази введені для обміну і розміщення в запропонованій СКП спеціалістів курси інших виробників (рис. 1).

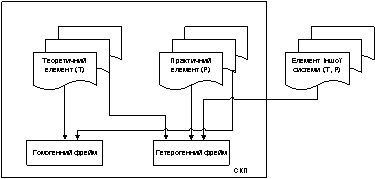
Рисунок 1 - Компоновка даних СКП спеціалістів

З такої точки зору модель фрейму має вигляд:

, (6)

де - функція формування фрейму, виконується в автоматизованому модулі обробки даних – АМОД; _{- зовнішній теоретичний матеріал;} – _{зовнішній практичний матеріал.} Вираз (6) допускає різні варіанти реалізації фрейму в залежності від потужності кожної з підмножин. Дамо коротку характеристику деяким типам фреймів.

Теоретичний фрейм () містить тільки теоретичні відомості. З таких фреймів складаються довідники, енциклопедії, або електронні версії підручників та книг. Варіанти теоретичного фрейму можна записати такими виразами:

Практичний фрейм () містить елементи ілюстративного характеру (наприклад, відео, аудіо) або контролюючого характеру. Такі фрейми використовуються для систем онлайн-тестів, презентацій, частково для інтерактивних підручників, заснованих на слайд-шоу, або відеозаписах. Варіанти практичних фреймів можна записати:

Загальний фрейм (). Загальний випадок фрейму, в якому можуть бути елементи даної системи, і можуть залучаються матеріали з інших джерел:

Чистий гомогенний фрейм (). Ці фрейми повністю складаються з елементів, які входять до даної СКП спеціалістів. Гомогенні фрейми характерні для тих систем, які поширюються на статичних носіях (таких як CD-ROM, DVD, або на носіях типу flash), а також для тих курсів підготовки, які виконуються на замовлення під конкретну задачу:

Чистий гетерогенний фрейм (). Такі фрейми, частіше за все, застосовуються в СКП, орієнтованих на самостійну роботу студента з Internet-ресурсами:

Вироджений фрейм (). Так звані, пусті фрейми, тимчасово використовуються при заміни старих фреймів новими, чи тих, які знаходяться на доопрацюванні:

Таким чином, АКП вважатимемо множину фреймів, які складають цілісну систему навчальної інформації з дисципліни. Враховуючи вищенаведене, можна визначити курс як множину фреймів

.

В множині К слід виділити підмножину фреймів, які містять базові знання, що становлять фундаментальну основу курсу (таких підмножин може бути і декілька, за бажанням розробника АКП). Фундаментальною основою курсу вважатимемо множину фреймів F, які містять інформацію, необхідну і достатню для отримання суб¢єктом підготовки знань з деякої дисципліни [4]:

. (7)

Умовою відповідності курсу вимогам даної дисципліни можна розглядати наявність у даному курсі К підмножини

,

де може містити посилання на інші ресурси в межах даного АКП (рис. 2).

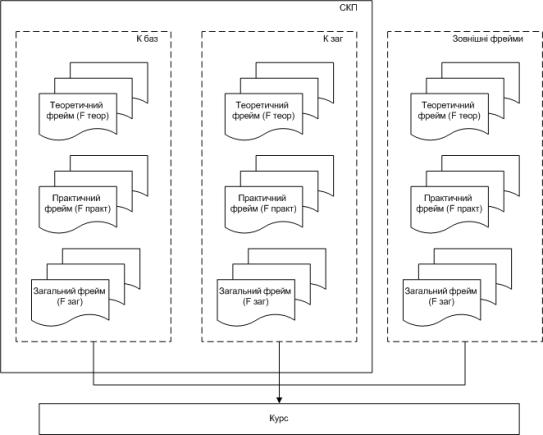
Рисунок 2 – Компоновка курсу підготовки

Введемо деякі означення, які будуть необхідними в подальшому.

Курс К забезпечує суб¢єкту підготовки необхідний та достатній рівень знань з даної дисципліни, якщо для цього курсу виконується рівність , інакше – академічно неповним.

Якщо для даної фундаментальної основи існують два курси та , такі, що , і , то такі курси називають академічно спорідненими.

Якщо для даної фундаментальної основи існує такий курс , що , то такий курс називається елементарним.

Якщо для даної фундаментальної основи існує такий курс , що , то такий курс називається поширеним.

Якщо для двох курсів та існують фундаментальні основи та , такі, що , то перший курс називається фундаментальним, а другий - похідним.

Якщо для двох курсів та існують фундаментальні основи та , такі, що , але то такі курси називаються близькими.

Очевидно, що НМ курсу підготовки, побудовані за традиційною схемою майже завжди є елементарними, а більшість АКП, які складають основу СКП спеціалістів, мають складнішу природу.

Висновки

У даній роботі формалізовано поняття АКП. Використовуючи теорію фреймових представлень знань, поряд із звичним визначенням теоретичного, і практичного фрейму, вперше введено поняття гомогенного, чистого гомогенного, гетерогенного, виродженого фрейму для подальшої можливості генерування фреймів динамічно, відповідно індивідуальним даним діяльності суб¢єкта підготовки. Вдосконалено поняття АКП та запропоновано нові поняття – фундаментального, академічно спорідненого, елементарного, поширеного, похідного курсів, поняття близьких курсів, що дало потенційну можливість аналізувати ступінь опанування суб¢єктом підготовки дисципліни, базуючись на аналізі структури опанованих ним матеріалів.

Литература

1. Weber G., Specht M. User Modeling and Adaptive Navigation Support in WWW-Based Tutoring Systems // User Modeling: Processings of the Sixth International Conference, UM97 – Vienna. New York. CISM. 1997.

2. Гороховський О. І., Снігур А. В., Трояновська Т. І. Розробка формалізованого опису автоматизованої системи дистанційного навчання // Інформаційні технології та комп’ютерна інженерія №1(8), 2007. Вінниця, ВНТУ, 2007. С. 235-239: іл.1.

3. Гороховський О. И., Трояновська Т. И., Каюмов Ю. П. Фреймовая основа дистанционного обучения // «Гражданская авиация на современном этапе развития науки, техники и общества», МНТК 18-19 мая 2006, г. Москва. М.: МГТУГА, 2006. – с.272-276.

4. Гороховський О. І., Трояновська Т. І. Моделі складових АСДН // Вісник Хмельницького національного університету, 2009, № 3. Хмельницький, ХНУ. С. 230-236.