Ковалец О.Я.
Национальный технический университет Украины «КПИ»
УРАВНЕНИЯ
ЦИЛИНДРИЧЕСКОГО ПОДВЕСА В ПЕРЕМЕЩЕНИЯХ. БЕЗРАЗМЕРНАЯ ФОРМА
Уравнения цилиндрической
оболочки в безразмерной форме имеют вид:
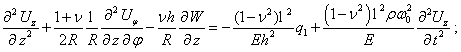 (1)
(1)
![]() (2)
(2)
![]()
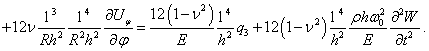 (3)
(3)
Не будем, пока
что, рассматривать конкретную расчетную схему, а изложим общую теорию
интегрирования полученных дифференциальных уравнений.
Логическим продолжением уже полученного служит построение методических
и математических предпосылок для выполнения приближенного интегрирования
уравнений подвеса. Суть предлагаемого метода изложим в самом общем виде.
Принимаем, что поверхность поплавка нагружена произвольным внешним
динамическим воздействием (распределенным, или сосредоточенным – в точке, по
линии, по площади и т.п.). Считаем также, что на краях поплавка (z=0, z=1) заданы некоторые
граничные условия – кинематические, геометрические или силовые.
Излагаемый метод предусматривает выполнение двух этапов:
-
вначале
проводится процедура разделения переменных в уравнениях движения при помощи
метода Фурье;
-
затем
используется метод Бубнова-Галеркина.
Поскольку рассматриваются
замкнутые оболочки вращения, то в окружном направлении (вдоль параллели)
следует ожидать периодичности силовых, кинематических полей, то есть они должны
определенным образом зависеть от периодических функций типа cos kφ,
sin kφ (k = 0,1,…). В свою очередь,
внешнее динамическое нагружение по трем направлениям может быть и
непериодическим по координате φ.
Но нагрузки
![]()
всегда можно, во всяком случае формально, представить в виде рядов Фурье по координате φ.
Поэтому считаем, что
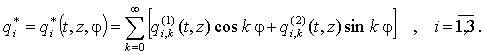 (4)
(4)
В соответствии с этим и
структура координатных функций будет иметь вид:
![]()
![]() (5)
(5)
![]()
Вначале представим их следующим образом:
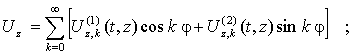 (6)
(6)
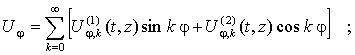 (7)
(7)
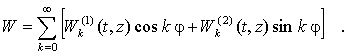 (8)
(8)
Соотношения
(4), (6 – 8) подставим в дифференциальные уравнения (1 – 3) и проведем процедуру
разделения переменных методом Фурье для каждого из деформированного состояний.