Ковалец О.Я.
Национальный технический университет Украины «КПИ»
РАЗДЕЛЕНИЕ
ПЕРЕМЕННЫХ В ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЯХ ПОПЛАВКА МЕТОДОМ ФУРЬЕ. ЦИКЛИЧЕСКОЕ ДЕФОРМИРОВАННОЕ СОСТОЯНИЕ
Продольные перемещения.
![]()
![]() 1
1 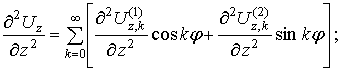
![]()
![]()
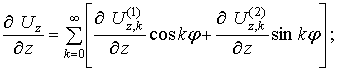
![]()
![]()
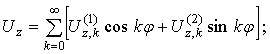
![]()
![]()
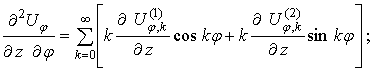
![]()
![]()
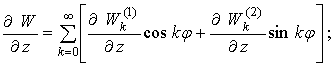
![]() -1
-1 ![]()
![]() 1
1 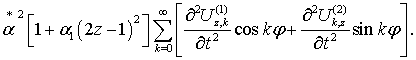 (1)
(1)
Сгруппируем слагаемые,
содержащие ![]() и
и ![]() .
.
Получаем:
![]()
![]() ,
,
![]() (2)
(2)
![]()
![]()
![]() (3)
(3)
Окружные
перемещения.
![]() 1
1
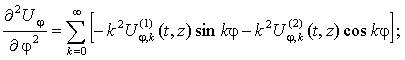
![]()
![]()
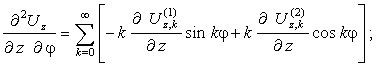
![]()
![]()
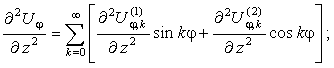
![]()
![]()
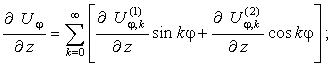
![]()
![]()
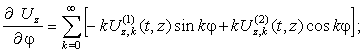
![]()
![]()
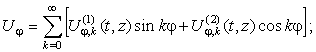
![]()
![]()
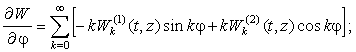
![]() 1
1 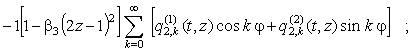
![]() 1
1 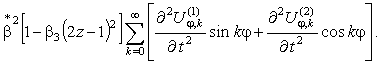
Сгруппируем слагаемые с ![]() и
и ![]() :
:
![]()
![]()
![]() (4)
(4)
![]()
![]()
![]()
![]() (5)
(5)
Радиальные
перемещения.
![]()
![]()
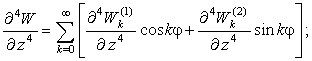
![]()
![]()
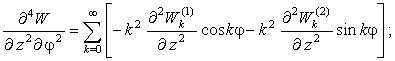
![]()
![]()
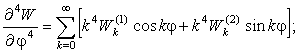
![]()
![]()
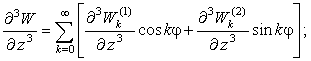
![]()
![]()
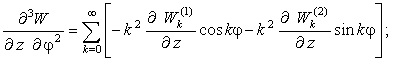
![]()
![]()
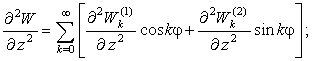
![]()
![]()
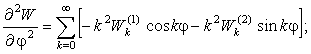
![]()
![]()
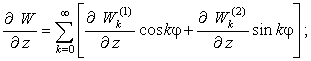
![]()
![]()
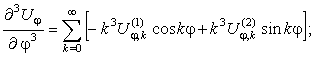
![]()
![]()
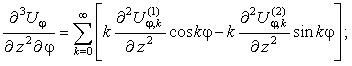
![]()
![]()
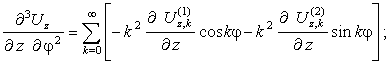
![]()
![]()
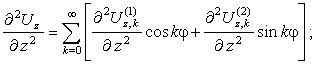
![]()
![]()
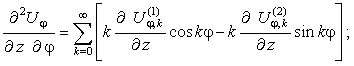
![]()
![]()
![]()
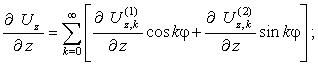
![]()
![]()
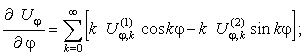
![]()
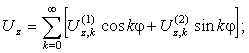
![]() 1
1 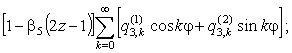
![]() 1
1  (6)
(6)
Сгруппируем слагаемые, содержащие ![]() и
и ![]() :
:
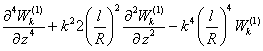
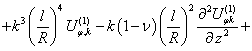
![]()
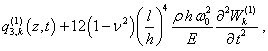
![]() (7)
(7)
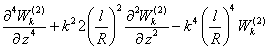
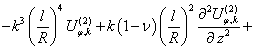
![]()
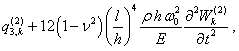
![]() (8)
(8)
Обращает на
себя тот факт, что при циклическом нагружении уравнения продольных перемещений
содержат слагаемое с коєффициентом “![]() ” в первой степени,
уравнения для окружных перемещений – два слагаемых с параметром “
” в первой степени,
уравнения для окружных перемещений – два слагаемых с параметром “![]() ”, в одном случае это “
”, в одном случае это “![]() ”, в другом “
”, в другом “![]() ” в первой степени. Наконец, в уравнениях радиального
перемещения поверхности присутствуют пять слагаемых с параметром “
” в первой степени. Наконец, в уравнениях радиального
перемещения поверхности присутствуют пять слагаемых с параметром “![]() ”:
”:![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
С увеличением
числа циклов, как следует из уравнений движения, на продольное перемещение ![]() все большее влияние
оказывают окружные перемещения
все большее влияние
оказывают окружные перемещения ![]() . Причем это влияние возрастает по линейному закону.
. Причем это влияние возрастает по линейному закону.
В то же
время, на величину окружных перемещений ![]() , в свою очередь, линейно влияют продольные перемещения
, в свою очередь, линейно влияют продольные перемещения ![]() . Увеличение свободного члена
. Увеличение свободного члена ![]() растет по
параболическому закону. Очевидно, что в этом случае наблюдается стремительное
увеличение частоты собственных колебаний.
растет по
параболическому закону. Очевидно, что в этом случае наблюдается стремительное
увеличение частоты собственных колебаний.
Наиболее
заметно влияние увеличения числа циклов на радиальные перемещения ![]() . Это кубическая зависимость от окружних перемещений
. Это кубическая зависимость от окружних перемещений ![]() . Кроме того, в четвертой степени растет собственная частота
радиальных перемещений. Пояснение этому факту состоит в значительно меньшей
жесткости оболочки в радиальном направлении по сравнению с двумя другими.
. Кроме того, в четвертой степени растет собственная частота
радиальных перемещений. Пояснение этому факту состоит в значительно меньшей
жесткости оболочки в радиальном направлении по сравнению с двумя другими.