Математика/ 4. Прикладная математика.

к.ф.-м.н. Мухамбетжанов А.Т.

Евразийский национальный университет им. Л.Н. Гумилева, Казахстан

Об одном методе приближенного решения линейных краевых задач в одномерном случае

Пусть Ω ограниченная область, принадлежащая R с гладкой границей

∂Ω. Рассмотрим задачу

Lu = -u" + q(x)u = f(x),

(1)

где f(x) L₂(Ω). Построим решение, используя метод, который рассмотрен в работах /1/. Введем оператор А₀, следующим образом: -u"=v, или в операторной форме A₀u = v, где оператор однозначно разрешим в пространстве L₂ (Ω) с заданными краевыми условиями.

Тогда уравнение (1) примет вид:

(1’)

Если v найдено, то и вычисляется по формуле и = .

Обозначим

(2)

При ω = v, где v - решение (1’) имеем J(ω) =0.

Будем предполагать, что уравнение (1’) для любой правой части f(x) L₂(Ω) имеет единственное решение. Следовательно, из теоремы Бaнаха вытекает, что

(2)

где М = Е + q(x) . (3)

Построим итерационный процесс. Пусть ω_п п-ное приближенное решение уравнения J(ω_n)=0. Положим

ω_п+1= ω_n – εω, ||M||^-2 ≥ ε, ε > 0

Тогда

Выберем ω = M*(Mω_n – f ). В силу условия (2) имеем

(4)

Поэтому из (4) следует

Выберем , Тогда получим

(5)

Для разности имеем

Это неравенство и (5) дают следующий результат:

Теорема 1 Пусть для любого f(x) (1) имеет единственное решение и , причем оператор М, определенный по (1’), удовлетворяет условиям , _, причем справедливо неравенство cd >1. Тогда для любого последовательность , определяемая по формулам

сходится к решению ω. уравнения (1’) причем выполнены оценки

где При этом функция и = А^-1ω будет решением задачи (1).

Рассмотрим непрерывный аналог описанного дискретного случая.

Считая зависящим от параметра t (0,), продифференцируем J() по t:

(6)

Выберем , из уравнения

(7)

Тогда из (6) вытекает . В силу этого равенства, а также из ограниченности определим J () и М.

Имеем . Проинтегрируем обе части неравенства по t:

Отсюда . Для решения (7) имеем

, (8)

где B = M*M/2,

Последняя формула дает экспоненциальную сходимость (t) к пределу при . Хотя абстрактная формула (8) выписана явно, вычисление значения (t) пo (8) не менее трудно, чем решение исходной задачи, то есть можно получить счетное множество решений. Но нам не нужны все значения (t) для , нам достаточно знать его предел при . Прямой переход к пределу в (8) приведет нас к исходной задаче, так как.По этим причинам необходимо формулу (8) заменить другой эффективно вычисляемой формулой, имеющей одинаковый предел при c (t).

Замечание 1 Из теоремы 1 при расчете по рекуррентным формулам не всегда удается иметь хорошую оценку . Поэтому нужно поступать следующим образом:

Берем любое и начинаем вычисления и J(). Этим значением пользуемся до тех пор, пока выполняется

.

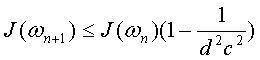Если при некотором п это неравенство нарушается, то меняем на и продолжаем счет и т.д.

Замечание 2 Согласно (6) имеем

(9)

Правая часть получает минимальное значение при

(10)

Поэтому для определения последовательности можно использовать рекуррентную формулу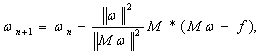

где Эта формула сложнее формулы, предложенной в теореме 1, но при ее использовании итерационный процесс сходится быстрее, нет необходимости вычислять нормы M и , а достаточно знать их ограниченность. Отметим также, что если выбрано по формуле (10), то

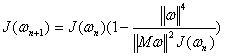
а величина в скобке не больше единицы. Действительно, если обозначим

то имеем

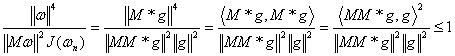
равенство этой величины возможно только, если.

Литература:

1. J. M. Ortega, Introduction to parallel and vector solution of linear systems, Plenum Press, New York, 1982.

2. H. Trielel, Approximation nubers in function spaces and the distribution of eigenvalues of some fractal elliptic operators, J. Approximation Theory, 129 (2004), 1-27.