Математика /4. Прикладная математика/

Рябоштан А.Ф., к.т.н. Миленин А.Н.

Харьковский национальный технический университет сельского хозяйства

имени П. Василенка

Описание порции поверхности второго порядка гладкости

Пусть заданы ребра пространственного криволинейного четырехугольника (порции поверхности) таким образом, что противоположные две его стороны зависят от параметра u (uÎ[0,1]), оставшиеся две – от v (vÎ[0,1]). Уравнение произвольной линии порции поверхности для i- ой координаты x_i (i=1,2,3) будем обозначать (u, v). Стороны порции поверхности описываются функциями (u, 0)_і, (u, 1)_і, (0, v) _і, (1, v) _і i=1,2,3.

Запишем уравнение порции поверхности двумерного обвода для i- ой координаты в виде (индекс координаты опускаем):

, (1)

где L(u) – матрица-строка.

, (2)

где l_i – переходные функции, которые обеспечивают выполнение заданных дифференциальных условий;

L'(v) – матрица-столбец, транспонированная по отношению к L(u), её функции l_i(v) зависят от v.

Структура функций (u, 0)_v и (u, 1)_v определяет направление поперечных касательных вдоль ребер (u, 0) и (u, 1), то есть касательные для линий, соединяющих соответственные точки указанных ребер. При u = 0 их значения должны совпадать со значениями производной вдоль ребра (0, v) соответственно при v = 0 и v = 1. Поэтому их можно принять следующими:

, (3)

Функция l₁(u) имеет l₁(0) = 1, l₁(1) = 0 и нулевые значения своих производных до второй включительно при u = 0 и u = 1, что обеспечивает выполнение требования согласования значений функции в узлах порции поверхности. Проведя аналогичные рассуждения, имеем:

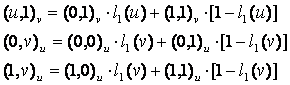(4)

Здесь , , , – значения производных по u функций (u, 0), (u, 1) в соответствующих узлах порции поверхности; , , , – значения производных по v функций (0, v), (1, v) в тех же узлах.

Аналогичным образом определяем функции:

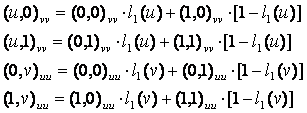, (5)

где , , , – значение вторых производных по v функций (0, v), (1, v) в узлах порции поверхности;

, , , – значения вторых производных по u функций (u, 0), (u, 1) в тех же узлах.

Дифференцируя (3) по u , имеем:

, (6)

что даёт . Аналогично имеем равенство нулю смешанных производных , , , , , , в узлах порции поверхности. В общем случае функции поперечных первых и вторых производных должны выбираться с обязательным условием совместимости их значений в узлах, а именно:

,

, (7)

,

Функции (3), (4) и (5) позволяют осуществить стыковку порций поверхности с соблюдением второго порядка гладкости на границах порций при нулевых значениях смешанных производных в узлах. Рассмотрим, каким образом осуществляется выполнение граничных условий. Запишем уравнение (1) схематично следующим образом:

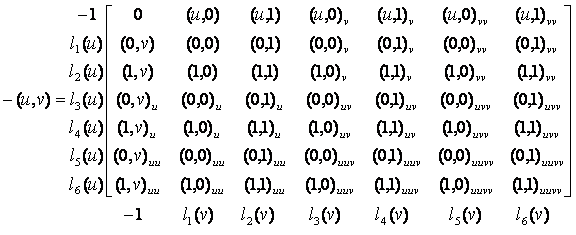(8)

Запись означает, что уравнение представляет собой сумму членов матрицы, умноженную на соответствующие множители l_і(u) (слева) и l_і(v) (снизу). Положим u = 0. Тогда l₁(0)=1, остальные l_і(0)=0, і = 2¸6, что выделяет в матрице вторую строку, все члены которой, кроме (0, v), соответственно равны членам первой строки (при u = 0) с противоположным знаком, то есть при суммировании они сокращаются, независимо от значений функции l_і(v), і = 1¸6. Имеем (0, v) = (0, v). Значение u = 1 выделяет третью строку матрицы, члены которой сокращаются при суммировании с членами первой строки, что приводит к равенству (1, v) = (1, v).

Положим v = 0. Тогда l₁(v) = 1, остальные l_і(0)=0, і = 2¸6, что выделяет в матрице второй столбец, все члены которого при суммировании сокращаются с членами первого столбца, за исключением (u, 0). Имеем (u, 0) = (u, 0). Аналогично при v = 1 имеем (u, 1) = (u, 1).

Взаимное сокращение членов соответствующих строк и столбцов оказалось возможным вследствие указанной ранее структуры функций «поперечных» первых и вторых производных на границах порции поверхности.

Дифференцируем (8) по u. Функции l_і(u) по u заменяются их производными l_і`(u), функции в первой строке матрицы также будут заменены их производными: ,, …, .

Равенство u = 0 выделяет четвертую строку матрицы, члены которой взаимно сокращаются с членами первой строки так, что имеем = . Аналогично u = 1 дает = . При v = 0 выделяется второй столбец, члены которого, за исключением , сокращаются с членами первого столбца, так что =. При v = 1 имеем=.

Определяем вторую смешанную производную, дифференцируя полученное выше уравнение по v. При этом члены строки l_і(v) заменяются их производными l_і`(v), функции первого столбца будут , , …, .

При u = 0 l₃`(0) = 1, остальные l<sub>і</sub>`(0) = 0, что выделяет четвертую строку матрицы, члены которой взаимно сокращаются с членами первой строки. Имеем =. При v = 0 l₃`(0) = 1, l<sub>і</sub>`(0) = 0. При совместном рассмотрении первого и четвертого столбцов имеем =. Аналогично выполняются остальные граничные условия по второй смешанной производной.

Решение задачи для второй производной по u (или v) вызывает необходимость согласования вторых производных от функций «поперечных» касательных и вторых производных в узлах порции поверхности. В рассматриваемом случае это согласование выполняется автоматически вследствие нулевых значений указанных производных в узлах, что обеспечивается функцией l₁ в уравнениях (4) и (5). Здесь речь идёт о смешанных производных по параметрам u и v для определенной координаты х_і.

Смешанная производная порции поверхности в пространстве в его узлах в общем случае не будет иметь нулевых значений. В рассматриваемом уравнении (8) блок (4´4) членов матрицы в правой нижней её части (значения смешанных производных , …) можно заменить нулями. Если по условиям задачи требуется, чтобы смешанные производные по параметрам (для определения координаты х_і) имели нулевые значения в узлах порции поверхности, то в уравнениях (4) и (5) необходимо функцию l₁ заменить другой функцией, обеспечивающей выполнение заданных значений смешанных производных.

Приведенный способ описания порций поверхности второго порядка гладкости позволяет достаточно успешно описывать межлопаточное пространство газовых турбин, как описание граничных поверхностей порций пространства.