Химия и химические технологии / 5. Фундаментальные
проблемы создания новых материалов и технологий
С.М.Ерменов, А.А.Волненко,
Н.Т.Сейтханов, М.А. Жусупалиев.
ЮКГУ им.М.Ауезова, г.Шымкент
Моделирование и расчет скорости газа в аппарате с пирамидальными
контактными устройствами
Для турбулентного движения, как показали многочисленные теоретические и
экспериментальные данные [1-8], в частности в контактных устройствах
массообменных аппаратов, характерна пульсация динамических характеристик.
Проведением усреднения для скорости и давления по времени система Навье-Стокса
преобразовывается в систему Рейнольдса. Для ее замыкания необходимо привлекать
зависимости между пульсациями скоростей, для которых характерна нестационарность.
В работах Иевлева В.М.
[5] поставлена и решена задача об определении крупномасштабных турбулентных
пульсаций. Основной смысл этого подхода заключается в следующем. Случайные силы
Fi,, входящие в уравнения Навье-Стокса, заменяются их
осредненными значениями. Таким образом, при решении соответствующих
уравнений рассчитывается поле скоростей, отличающееся от истинного, но имеющее
одинаковые с ним статистические характеристики. Данный прием равносилен замене
случайной величины (в данном случае, например, скорости) ее математическим
ожиданием. Далее эти средние величины, полученные осреднением случайных значений пульсационных величин Fi, для
определенной группы точек, используются в качестве “центральной” для трехмерной
расчетной сетки. Однако, в контактных устройствах пирамидальной формы, как
показывают эксперименты, разброс динамических характеристик велик, они
изменяются в широких интервалах, поэтому их замена средними значениями
фактически означает неоправданное упрощение гидродинамики для разных зон
контактного устройства.
Преимущества моделей Прандтля и Колмогорова объединяет модель
Колмогорова-Прандтля.
![]() , (1)
, (1)
где ![]() - кинетическая энергия турбулентных
пульсаций,
- кинетическая энергия турбулентных
пульсаций,
![]() = сonst, l- масштаб
турбулентности.
= сonst, l- масштаб
турбулентности.
Из
анализа различных моделей турбулентности [6-8]
можно сделать вывод о том, что математическая модель турбулентного течения
в контактном устройстве пирамидальной формы состоит из уравнения неразрывности,
уравнения Рейнольдса, уравнений относительно турбулентных пульсаций,
замыкающего соотношение для k и ![]() , а также граничных условий для динамических функций. Уравнения турбулентности для кинетической энергии к(х, у), локального масштаба l(х, у),
функции тока
, а также граничных условий для динамических функций. Уравнения турбулентности для кинетической энергии к(х, у), локального масштаба l(х, у),
функции тока ![]() (х, у), завихренности
(х, у), завихренности ![]() (x,y) записываются в одном и том же виде. Это является
важным качеством этого метода, т.к. появляется возможность разработки универсального
алгоритма решения совместной системы уравнений для динамических характеристик и
включения в нее уравнений для других неизвестных (например, температуры и концентрации
вещества). Этим методом было решено большое количество практических задач, результаты
сравнивались с большим количеством экспериментальных данных разных авторов.
Полученные аналитические и численные решения, по постановке задачи и целей,
особенностям течения эти задачи близки к рассматриваемой нами. Метод обладает
абсолютной вычислительной устойчивостью, т.е. независимо от соотношений между
пространственными и временными шагами конечно-разностной сетки через
определенное количество итераций можно получить приближенные численные значения
динамических характеристик с требуемой точностью, что при разработке инженерных
методик расчета динамических характеристик потоков имеет большое значение, т.к.
отпадает необходимость для каждого комплекса параметров решения проверять
условия сходимости и устойчивости.
(x,y) записываются в одном и том же виде. Это является
важным качеством этого метода, т.к. появляется возможность разработки универсального
алгоритма решения совместной системы уравнений для динамических характеристик и
включения в нее уравнений для других неизвестных (например, температуры и концентрации
вещества). Этим методом было решено большое количество практических задач, результаты
сравнивались с большим количеством экспериментальных данных разных авторов.
Полученные аналитические и численные решения, по постановке задачи и целей,
особенностям течения эти задачи близки к рассматриваемой нами. Метод обладает
абсолютной вычислительной устойчивостью, т.е. независимо от соотношений между
пространственными и временными шагами конечно-разностной сетки через
определенное количество итераций можно получить приближенные численные значения
динамических характеристик с требуемой точностью, что при разработке инженерных
методик расчета динамических характеристик потоков имеет большое значение, т.к.
отпадает необходимость для каждого комплекса параметров решения проверять
условия сходимости и устойчивости.
Основой предлагаемого
нами метода является использование основного дифференциального уравнения для
функции φ(х,у), которая является обобщенной и равняется одной из функций ψ(х,у), ω(х,у), k(x,y), l(x,y), полностью определяющих гидродинамику в контактной
зоне. Система определяющих уравнений имеет вид:
![]() , (2)
, (2)
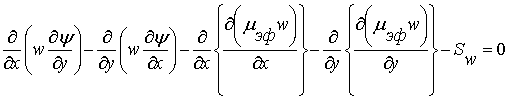 , (3)
, (3)
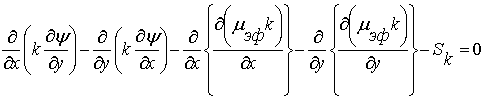 , (4)
, (4)
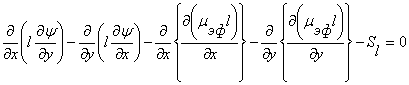 . (5)
. (5)
Уравнения (2)-(5) относятся к типу эллиптических уравнений математической
физики. В [5]
показано, что в областях с
ограниченными границами, аналогичных с контактными устройствами пирамидальной
формы и с соответствующими граничными условиями 1-и 2-рода они имеют
единственные решения, устойчивыми относительно начальных условий.
Краткая
последовательность расчёта функции тока, завихрённости, кинетической энергии и
масштаба турбулентности для области решения в форме усеченной пирамиды представлена
следующим образом:
1.
Для начального момента времени
задаем значения j во внутренних узлах (jj,i = yj,i, wj,i, kj,i, lj,i).
2.
По формулам находим
значения Aji, Bji, Cji, Dji.
Если для расчета во внутренних
точках значений динамических функций
требуются их значения на границе, то используются соответствующие
аппроксимации. Для граничных узлов использовали соотношение:
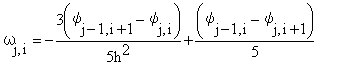 (6)
(6)
3.
Вычисляем значения jj,i для
следующего момента времени.
4. Проверяли условие
выполнения точности.
5. По найденным
функциям j определяли профиль скорости, перепад давления,
эффективную вязкость, кинетическую энергию и другие динамические величины.
6. Исследование
зависимости гидравлического
сопротивления от числа Рейнольдса, соотношений между шагами в
вертикальном и горизонтальном направлении,
также от плотности орошения проводится вычислением численного значения
интеграла от диссипации по двумерной области:
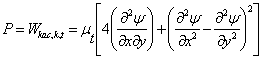 (7)
(7)
Использование этой функции позволяет без
решения уравнения для давления находить гидравлическое сопротивление в
контактной зоне. Интегрированием Р по всему объему по формуле Симпсона нами
найдено гидравлическое сопротивление пирамидального контактного устройства.
Проведены систематические численные эксперименты, для разных чисел Рейнольдса
от 103 до 105, соответствующих среднерасходным скоростям
рабочего режима аппарата.
На каждом временном шаге нами для учета
влияния пленки жидкости на граничное взаимодействие вместо условия прилипания
использовано соотношение
Uг=-uж, (8)
где uж – скорость пленки жидкости на стенке;
Uг – скорость газа на стенке.
В
уравнении (8) знак «-» взят с целью учета общего противотока газа и жидкости.
Литература
1.
Кутателадзе С.С. Пристенная турбулентность, -Новосибирск: Наука,1973.
–345 с.
2.
Абрамович Г.Н. Теория турбулентных струй. -М.: Наука. –1960.-534с.
3.
Гиневский А.С., Федяевский К.К. Расчет характеристик турбулентной струи
// Изв.АН СССР.-1959.3. –С.234-241.
4. Холпанов Л.П., Мочалова Н.С.,
Вороненко Г.В. Математическое моделирование течений в аппарате с неподвижным
зернистым слоем. //ТОХТ.-1995.- 29, 2.-С. 166-179.
5.
Иевлев В.М. Численное
моделирование турбулентных течений. -М: Наука, 1990., -215с.
6.
Бэтчелор Дж. Теория однородной турбулентности. –М: Иностр.лит-ра,1955.
–198с.
7. Chapman D.R. Druden lecture: Computational Aerodynamic Developmentand
//AIAA Journal.-1979,17, 1213-1313.
8.
Онуфриев А.Т. Об уравнениях
полуэмпирической теории турбулентности
// ЖПХ иТФ - 1970. 2. -С.66-71.