Математика/ 4. Прикладная математика

Фазылова Л.С., Мукимбекова Д.М.

Карагандинский государственный университет им. Е.А. Букетова, Казахстан

Применение системы MathCad для решения задач условной оптимизации

Применение новых информационных технологий в учебном процессе позволяет повысить не только эффективность, но и качество подготовки специалистов. При подготовке специалистов высшей квалификации по специальности «Математическое и компьютерное моделирование» изучение численных методов решения задач на условный экстремум является важной частью курса «Методы оптимизации» [1]. Применение пакетов прикладных программ, таких как MathCad, Matlab, для решения задач данного типа во много раз ускорит учебный процесс и позволит студентам приобрести навыки математического и компьютерного моделирования различных оптимизационных задач.

В данной работе рассматриваются вопросы применения системы MathCad (МС) при решении задач на условный экстремум. Для нахождения локальных или глобальных экстремумов в системе MathCad используются функции Minimize и Maximize [2]. Сложность заключается в выборе начальной точки и указании области, в которой ищется экстремум.

Во-первых, нужно задать функцию. Возьмем функцию

.

Вызовем панель Graph. Построим график функции. По рисунку 1 видно, что минимумов несколько.

Однако по рисунку их положение определить сложно. Значительно больше информации получим, построив линии уровня функции. Это тоже можно сделать с помощью системы МС. Нажмем на панели Graph кнопку с изображением линий уровня.

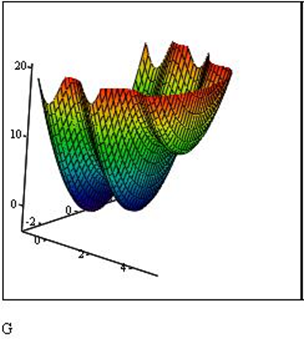
Рис 1

Возникнет шаблон, как и при построении графика. Впишем в шаблон имя функции и щелкнем мышью за пределами блока. Полученный чертеж можно улучшить. Во-первых, на линиях уровня можно указать значение функции. Для этого нужно вызвать окно форматирования, вкладку Special и на ней установить флажок Numbered. Результат представлен на рисунке 2.

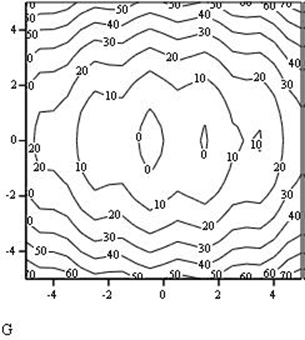
Рис. 2

Полученное изображение можно заполнить цветом, причем цвет будет соответствовать значению функции в точке. Соответствие цвета и величины значения такое же, как и на графике.

Для заполнения цветом нужно вызвать окно форматирования, выбрать вкладку Special и поставить флажок Fill. Чтобы не убирать окно форматирования, можно вместо клавиши OK нажать клавишу «Применить». Можно сделать линии уровня более гладкими. Для этого в окне форматирования нужно вызвать вкладку QuickPlot Data и заполнить позиции start, end, # of Grids. В нашем случае в столбце Range 1 поставим start − 4, end 4, # of Grids 40 и аналогично в столбце Range 2 (рис. 3).

Экстремумы функции будут находиться внутри самых маленьких замкнутых кривых. Из рисунка 3 видим, что один локальный экстремум нужно искать в области , а второй – в области , третий в области . По цвету видно, что максимальные значения находятся в угловых точках области.

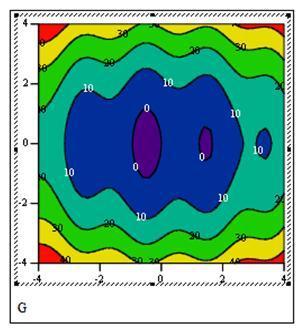
Рис. 3

Для нахождения одной из точек локального минимума зададим начальное приближение и сформируем вычислительный блок:

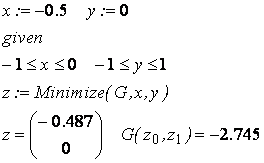
Получили, что первой точкой локального минимума является точка (−0.487; 0).

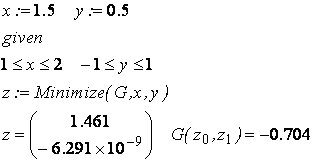
Видим, что вторая точка локального минимума − это точка (1.461; 0). Значение функции в ней больше, чем в предыдущей точке. Таким образом, предыдущая точка является точкой глобального минимума. При желании можете найти третью точку локального минимума и убедиться, что в ней значение функции еще больше.

Найдем теперь точки максимума:

Теперь результат соответствует действительности. Эта точка похожа на точку локального максимума. Однако проверим еще один угол нашей области:

Таким образом, наибольшее значение функции в области достигается в точке (−4; 4).

Заметим, что функция является четной по переменной y, поэтому то, что в точках минимума , можно было предсказать заранее, значение функции в точках (−4; −4) и (4; −4) можно не исследовать.

Не претендуя на новизну, авторы предлагают один из подходов к решению задач на условный экстремум, который основан на использовании графических возможностей и библиотек функций системы MathCad. Данный подход позволяет автоматизировать процесс решения задач оптимизации, дает возможность студентам эффективно осваивать материалы курса «Методы оптимизации» и может применяться в учебном процессе.

Литература:

1. Пантелеев А.В. Методы оптимизации в примерах и задачах: Учеб. пособие для студ. ВТУЗов/ Пантелеев А.В.. - М.: Высш.школа, 2008. - 544с.

2. Кирьянов Д. В. Мультимедийный учебник по Mathcad 14 - http://www.polybook.ru/mathcad/index.html.