К.т.н. Кучмистенко О.В., бак. Струж Б.А.

Івано-Франківський національний технічний університет нафти і газу, Україна

Математична модель сепарації в процесі гідроочищення гасу

Дослідження сепараційної установки як об’єкта автоматичного керування показали, що забезпечити необхідну ефективність процесу сепарації можна шляхом стабілізації основних режимних параметрів – рівня трьохкомпонентної суміші, рівня розподілу фаз суміш-вода і тиску газу в сепараторі. Розглянемо сепараційну установку, схема якої показана на рисунку 1.

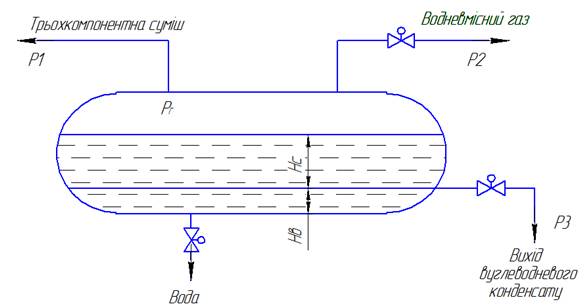
Рисунок 1 - Технологічна схема об’єкта керування

В нашому випадку трьохкомпонентна суміш подається наверх сепаратора, а вуглеводневий конденсат відбирається в певному місці збоку сепаратора.

Математичний опис процесу сепарації будемо робити виходячи з таких припущень:

– величини ,,,, які характеризують вміст води і газу в трьохкомпонентній суміші,постійні;

– температура рідкої фази в сепараторі не змінюється з плином часу;

– газ, що виділяється в результаті сепарації, підпорядковується законам ідеального газу;

– густини суміші і води, що знаходяться в сепараторі приймаються постійними;

– регулюючі органи системи керування встановлені на лініях газу, виходу вуглеводневого конденсату і дренажу води. Їх статичні характеристики ,,, де - гідравлічні опори клапанів;

Динаміка процесу сепарації. Рівняння матеріального балансу для трьохкомпонентної суміші запишемо так (рис. 2):

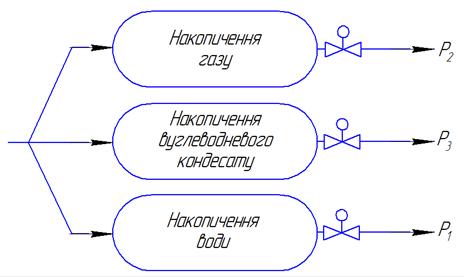
Рисунок 2 - Структурна схема матеріальних потоків сепаратора

[Швидкість накопичення суміші]=[Прихід суміші]-

-[Вихід вуглеводневого конденсату із сепаратора] (1)

[Швидкість накопичення суміші] =, (2)

де - маса трьохфазної суміші в сепараторі.

[Прихід суміші] = , (3)

де

, (4)

α – гідравлічний опір вхідного трубопроводу.

[Вихід вуглеводневого конденсату із сепаратора] =

=. (5)

де - віддаль від дна резервуару до місця під’єднання вихідного трубопроводу.

Підставляючи (2)-(4) в (1) отримуємо рівняння матеріального балансу для трьохкомпонентної суміші

. (6)

Складемо тепер рівняння матеріального балансу для води, що вилучається знизу апарата. Виходячи з загального рівняння матеріального балансу, будемо мати:

[Швидкість накопичення води] =, (7)

де - маса води в сепараторі.

[Прихід води] = , (8)

де величина m визначається формулою (4).

[Дренаж води] = (9)

Співвідношення (7)-(9) дають змогу записати рівняння матеріального балансу для води:

. (10)

Рівняння матеріального балансу для газової фази має вигляд, аналогічний (10).

[Швидкість накопичення газу]=[Прихід газу]-[Відбір газу] (11)

[Швидкість накопичення газу] =, (12)

де - маса газової фази в сепараторі.

[Прихід газу] = , (13)

де величина m визначається формулою (3.18).

[Відбір газу] =, (14)

де - густина газу при .

Підставляючи (12)-(14) в рівняння (11), приходимо до висновку, що

. (15)

Визначаємо маси і вуглеводневого конденсату і води, що знаходяться в резервуарі. Нехай - об’єм сепаратора, а - степінь його заповнення водою. Тоді об’єм, який займає вода, . Величина визначається розміщенням сепаратора в просторі. Для горизонтально розміщених сепараторів

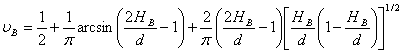, (16)

де - діаметр сепаратора.

Знаючи і , визначаємо масу води в сепараторі

. (17)

Аналогічно обчислимо масу суміші вуглеводневого конденсату і газу. Позначимо через степінь заповнення сепаратора рідкою фазою. Тоді вона займе об’єм

, (18)

де ,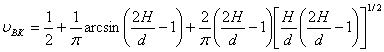

.

Отже,

і . (19)

Масу газу обчислимо, виходячи із закону стану ідеального газу

, (20)

де - мольна маса газу; - газова стала газу; Т- температура газу в градусах Кельвіна.

Об’єм, який займає газова фаза в сепараторі, обчислюється як:

Тоді

. (21)

Або враховуючи значення , запишемо

. (22)

Якщо допустити, що зміна температури в сепараторі незначна, то

, (23)

де .

З врахуванням значень , які визначаються формулами (17), (19) і (23), отримуємо таку математичну модель сепаратора:

(24)