Педагогические науки/ 5.Современные методы преподавания

Снежкина О.В., Бочкарева О.В., Ладин Р.А.

ПГУАС, филиал ВА МТО (г. Пенза), Россия

Реализация межпредметных связей

на примере транспортной задачи

С введением новых образовательных стандартов в учебных планах появилось много дисциплин, подразумевающих изучение математических методов и различных программных продуктов во взаимосвязи. Для оптимизации учебного процесса и обеспечения межпредметной взаимосвязи предлагается проводить занятия по принципу: одна задача – несколько решений. Реализацию этого принципа можно показать на примере транспортной задачи.

Пример. На три базы a _i поступил однородный груз в количестве: 100; 200; 90 тонн. Полученный груз требуется перевезти в три пункта b _j, потребности которых составляют: 190; 120; 30 тонн. Расстояние C_ij в ед.км. (i=1,2,3; j=2,2,3) между пунктами отправления и пунктами назначения приведены в табл.1.

Таблица 1.

b j a I	b 1=190	b 2=120	b 3=30
a 1=100	4	2	3
a 2=200	3	5	3
a 3=90	1	4	6

Рассмотрим решение транспортной задачи методом потенциалов при изучении дисциплины «Моделирование и оптимизация процессов» (направление подготовки «Технология лесозаготовительных и деревоперерабатывающих производств»).

Так как ∑a_i=100+200+90=390, ∑b_j=190+120+30=340, т.е. ∑a_i≠∑b_j , имеем открытую модель транспортной задачи, где суммарные запасы превышают суммарные потребности.

Математическая модель задачи формулируется следующим образом:

Найти min значение линейной функции при ограничениях

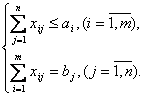
Данная открытая модель решается приведением к закрытой путем введения фиктивного потребителя, потребности которого b_n+1=∑a_I - ∑b_j=390-340=50. Стоимость перевозок для потребителя b_n+1 полагается равной нулю.

Составим первоначальный план перевозок, используя метод наименьшей стоимости, таблица 2.

Таблица 2.

b j a I	b 1=190	b 2=120	b 3=30	b 4=50
a 1=100	4	2 100	3	0
a 2=200	3 100	5 20	3 30	0 50
a 3=90	1 90	4	6	0

Проверяем оптимальность полученного плана перевозок методом потенциалов. Поставщику ставим в соответствие потенциалы U_i , а потребителюV_j и определяем их исходя из условия C_ij=U_i+V_j. Для всех свободных клеток находим ∆C_ij . Так как для свободных клеток все ∆C_ij≥0, то получен оптимальный план перевозок

,

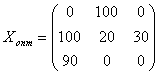обеспечивающий минимальную стоимость перевозок:

.

Теперь рассмотрим реализацию представленной транспортной задачи (таблица 1) при изучении дисциплины «Математические методы и модели в расчетах на ЭВМ». Решение задачи производим в программе Microsoft Excel . Создаем на Листе Excel таблицу с исходными данными и таблицу с изменяемыми ячейками, в которые будут записываться результаты плана перевозок (рис.1).

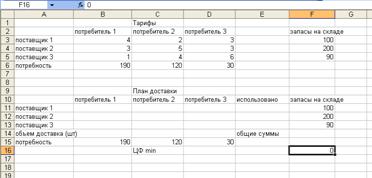
Рис. Фрагмент листа Excel с исходными данными

Для поиска оптимального плана перевозок, соответствующего минимальному значению ЦФ, воспользуемся надстройкой Поиск решения, активизировав параметры: линейная функция и неотрицательные значения. Результат выполнения поиска решения представлен на рисунке 2.

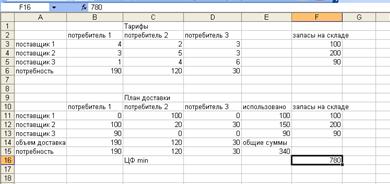
Рис.2. Результат расчета.

Предложенный метод организации учебного процесса позволяет студентам оценить, выделить преимущества каждого метода решения предлагаемой задачи и выбрать наиболее оптимальный.

Литература:

1. Бочкарева, О.В. Математические задачи как средство формирования профессиональных качеств личности / О.В. Бочкарева, Т.Ю. Новичкова, О.В. Снежкина, Р.А. Ладин // Современные проблемы науки и образования.–2014.–№2; URL :  www.science-education.ru/116-12584