Технические науки/ Авиация и космонавтика

Dr Nickolay Zosimovych

Shantou University, Shantou, China

INCREASING THE ACCURACY OF THE CENTER OF MASS STABILIZATION OF SPACE PROBE

Keywords: Space probe (SP), stabilization controller (SC), on-board computer (OC), gyro-stabilized platform (GSP), propulsion system (PS), angular velocity sensor (AVS), operating device (OD), space vehicle (SV), feedback (FB), control actuator (CA), control system (CS), angular stabilization (AS), center of mass (CM).

I. Introduction. In some cases, when using a control system built according to the principle of program control (the "robust trajectories" method) the efficiency of task solution is much influenced by the accuracy of the spacecraft stabilization system in the powered portion of flight. This concerns, for example, the trajectory correction phases during interplanetary and transfer flights, when the rated impulse execution errors during trajectory correction resulting from various disturbing influences on the spacecraft in the active phase, greatly affect the navigational accuracy. Hence, reduction of the cross error in the control impulse on the final correction phase during the interplanetary flight, facilitates almost proportional reduction of spacecraft miss in the "perspective plane". For example, in some space probes (SP) like Deep Impact [1, 2] and Rosetta missions [3, 4] reduction of cross error by one order during the execution of correction impulse (for modern stabilization systems this value shall be results in reduction of spacecraft miss in the "perspective plane" from 200 to 20 Such reduction of the miss accordingly increases a possibility of successful implementation of the flight plan, as well as the accuracy of the research and experiments conducted [5].

The Martian Moons Exploration (MMX) mission is scheduled to launch from the Tanegashima Space Center in September 2024. The spacecraft will arrive at Mars in August 2025 and spend the next three years exploring the two moons and the environment around Mars. During this time, MMX will drop to the surface of one of the moons and collect a sample to bring back to Earth. Probe and sample should return to earth in the summer 2029 [6].

Objectives: to solve the task of significant increase in stabilization accuracy of center of mass tangential velocities during the trajectory correction phases when using the "rigid" trajectory control principle.

Subject of research: The center of mass movement stabilization system in the transverse plane, which is used during the trajectory correction phases.

In order the control actions could be created during the spacecraft trajectory correction phase, a high-thrust service propulsion system with a tilting or moving in linear direction combustion chamber shall be used.

II. Content of the Problem. Functioning of the spacecraft movement stabilization channel in the transverse plane is based on the feedback principle, and together with the spacecraft this channel forms a closed deviation control system. We can consider two channels in this control system: an angular stabilization channel and center of mass movement stabilization channel (Fig. 1).

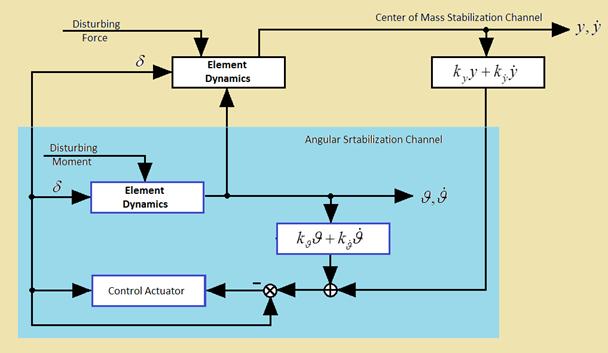
Fig. 1. Functional diagram of model spacecraft stabilization

The angular stabilization channel facilitates angular position of the spacecraft when exposed to disturbing moments. The center of mass movement stabilization channel is to ensure proximity to zero of normal and lateral velocities of the spacecraft under the influence of disturbing moments and forces. In most of the known (model) spacecraft stabilization systems [7-9] the control signal in the center of mass movement stabilization channel is generated according to proportional plus integral control law based on the measurements of tangential velocity of the center of mass and its integral-linear drift In the angular stabilization channel, the control signal shall be generated in proportion to the spacecraft deviation angle in the transverse plane and the angular velocity of the spacecraft rotation in this plane

The required dynamic accuracy of stabilization of tangential velocities in this system shall be achieved through the choice of the gain in the stabilization controller If the requirements to the accuracy of center of mass movement stabilization are stiff, the coefficients and shall be necessarily significantly increased [7]. However, if these coefficients are increased up to desired saturation, the system shall loose its motion stability, and further improvement of the accuracy of the spacecraft center of mass movement stabilization shall be impossible when this method of control is applied. This can be explained by the fact that the increase in the gain values in the center of mass movement stabilization channel results in improved performance of the channel, and the frequencies of the processes occurring in it become close to the frequencies of the angular stabilization channel, which fact enhances interaction of these two channels and makes it impossible to significantly improve the stabilization accuracy of the spacecraft center of mass tangential velocities in the control system concerned.

To improve the correction accuracy, the following additional algorithm shall be used in practice [9, 10]. The position of the steering control (turning PS) at the end of the previous active phase shall be memorized and set in its original position before PS is activated during next correction. The improvement of accuracy in this case shall be achieved by partial compensation of the main disturbing factors: eccentricity and thrust misalignment in the propulsion system already in the initial moment of operation of the propulsion system. This algorithm is based on the assumption that eccentricity and thrust misalignment in PS change slightly towards the end of the active phase during the previous correction, and PS setting before a new active phase sets in progress, ensures that the thrust vector goes approximately through the center of mass of the spacecraft, thereby considerably offsetting the disturbing moment. A similar algorithm was applied in the stabilization system of the Apollo spacecraft [11].

It should be pointed out that the process of implementation of the described algorithm is confronted by a number of challenges [5]:

· Difference in disturbing factors (moments and forces) during the previous and subsequent corrections results in additional errors in the stabilization of the tangential velocities of the spacecraft center of mass.

· Due to the limited time of the active phase, deactivation of PS during the previous correction may occur even before the completion of the transition processes in the stabilization system, and as a result, the system will remember the deviation of the steering control, which was not final.

Besides introduction of additional control algorithms, there are other ways to increase the accuracy of the center of mass movement stabilization. It is a commonly known fact that one of the ways to achieve high accuracy in automatic control systems, is to use the so-called invariant theory [12-14].

One of the problems inherent in the synthesis of invariant control systems, is the ability for the implementation of such systems in most cases through the use of the deviation control principle, as the simplest one and most widely used in practice. The publications [15-18] consider the possibility of constructing an invariant deviation control system with one adjustable parameter including an inertial element and a servo control with feedback. The general provisions of the invariant theory prove that no absolutely invariant system can be implemented in this case because this requires that the circuit with feedback should have an infinitely great gain.

As a rule, most invariant control systems are based on the use of the information about external influences. Such control systems belong to the class of combined regulatory systems. In particular, the combined systems constitute the majority of invariant systems [19-25].

There is still another method to enforce implementation of invariance conditions without application of combined regulatory techniques [26]. This method is based on the dual-channel principle, which means that in order to ensure the absolute invariance of some adjustable value towards external influence, invariance with respect to the above influence should be ensured between the point of influence application and the measuring point. To implement such a system, it is necessary that two influence distribution channels should be present in the controlled element.

In order to improve the accuracy of the synthesized algorithms, we propose the application of self-configuring elements, which turn the operating device and X-axis of the spacecraft at angles recorded at the end of the previous active phase before a new active phase begins. The use of the above self-configuring elements in the synthesized invariant algorithms produces the maximum effect in increasing of the dynamic accuracy of tangential velocities stabilization as compared to similar techniques in the existing systems. This is due to the fact that the dynamic error of drift velocity in the synthesized algorithms, shall be largely determined by the initial conditions of the transition process due to the partial invariance of the algorithms proposed, which with the help of the mentioned self-configuring elements, can approach the values corresponding to the established mode as close as possible.

The publication provides analysis of stability of the synthesized control algorithms, proves availability of stability margins in partially invariant systems sufficient for practical implementation [5].

We propose an algorithm for selection of parameters of the stabilization controller, which facilitates minimization of maximum error during stabilization of the tangential velocity of the spacecraft center of mass while ensuring adequate stability margins in the system.

Conclusion. The publication provides analysis of stability of the synthesized control algorithms, proves availability of stability margins in partially invariant systems sufficient for practical implementation.

We propose an algorithm for selection of parameters of the stabilization controller, which facilitates minimization of maximum error during stabilization of the tangential velocity of the spacecraft center of mass while ensuring adequate stability margins in the system.

References

1. Deep Impact Launch. Press Kit, January, 2005, NASA, USA.

2. William H. Blume. Deep Impact Mission Design. Springler, Space Science Reviews, 2005, PP. 23-42.

3. Matt Taylor. The Rosetta mission, ESA, 2011.

4. Verdant M., Schwehm G.H. The International Rosetta Mission, ESA Bulletin, February, 1998.

5. Nickolay Zosimovych, Modeling of Spacecraft Centre Mass Motion Stabilization System. International Refereed Journal of Engineering and Science (IRJES), Volume 6, Issue 4 (April 2017), PP. 34-41.

6. https://www.cosmos.esa.int/documents/653713/1000951/01_ORAL_Yamamoto.pdf/c0143f57-5863-46da-bc00-e32e88be08a6 - Yamamoto, M.-Y., Observation plan for Martian meteors by Mars-orbiting MMX spacecraft. April, 11, 2017.

7. Управление и наведение беспилотных маневренных летательных аппаратов на основе современных информационных технологий / Под ред. М.Н. Красильщикова и Г.Г. Себрякова. – М.: ФИЗМАТЛИТ, 2003, 280 с.

8. Статистическая динамика и оптимизация управления летательных аппаратов: Уч. Пособие для вузов / А.А. Лебедев, В.Т. Бобронников, М.Н. Красильщиков и др. - М.: Машиностроение, 1985. - 280 с.

9. Стаббс Г., Пинчук А., Шлюндт Р. Цифровая Система стабилизации космического корабля “Аполлон”. – Вопросы ракетной техники, 1970, No 7.

10. Справочное руководство по небесной механике и астродинамике / Абалакин В.К., Аксенов Е.П., Гребеников Е.А. и др. Изадание 2-е, Наука, 1976, 864 с.

11. Robert G. Chilton. Apollo Spacecraft Control Systems, NASA Manned Spacecraft Control Houston, Texas, USA, 1965.

12. Jan Willem Polderman, Jan C. Willems. Introduction to Mathematical Systems Theory: A Behavioral Approach (Texts in Applied Mathematics), Springer; 2nd edition (October, 2008), 455 p.

13. Spasskii R. A. Invariance of a system of automatic control, Journal of Soviet Mathematics, June 1992, Volume 60, Issue 2, PP. 1343–1346.

14. Bassam Bamieh, Fernando Paganini, Munther A. Dahleh. Distributed Control of Spatially Invariant Systems, IEEE Transactions on Automatic Control, Vol. 47, No. 7, July 2002, PP. 1091-1107.

15. Репин А.И. Теория автоматического управления (Конспект лекций), Можайск, 2011, 150 с.

16. Бейнарович В.А. Инвариантные системы автоматического управления с релейным усилителем, Доклады ТУСУРа, №2 (21), Часть 1, Июнь 2010, СС. 70-73.

17. Richard C. Dorf, Robert H. Bishop. Modern Control Systems, Pearson, 12^th edition, 807 pp.

18. Silvia Ferrari, Robert F. Stengel. Online Adaptive Critic Flight Control, Journal of Guidance, Control, and Dynamics, Vol. 27, No 5, September-October, 2004, PP. 777-786.

19. The Electronics Engineer’s Handbook, 5ty Edition McGraw-Hill 19, 2005, pp. 19.1-19.30.

20. Polderman J.W., Willems J.C. Introduction to the Mathematical Theory of Systems and Control, 458 pp.

21. Feron E., Brat G., Garoche P-L., Manolios P., and Pantel M. Formal methods for aerospace applications. FMCAD 2012 tutorials.

22. Colon M, Sankaranarayanan S., and Sipma H.B. Linear invariant generation using non-linear constraint solving. In Proc. CAV, LNCS, PP. 420-432. Springler, 2003.

23. Souris J., Favre-Felix D. Proof of properties in avionics. In Building the Information Society, Vol. 156, pp. 527-535. Springler, 2004.

24. Hennet J.C., Trabuco Dorea Carlos E. Invariant Regulators for Linear Systems under Combined Input and State Constraints. Proc. 33^rd Conf. of Decision and Control (IEEE-CDC’94), Lake Buena Vista, Florida USA, Vol. 2, pp. 1030-1036.

25. Amaria Luca, Pedro Rodriguez, and Didier Dumur. Invariant sets method for state-feedback control design, 17^th Telecommunications forum TELEFOR 2009, Serbia, Belgrad, November 24-26, PP. 681-684.

26. Gazanfar Rustamov. Invariant Control Systems of Second Order, IV International Conference “Problems of Cybernetics and Informatics” (PCI’2012), September 12-14, 2012, Baku, PP. 22-24.