Математика/
5. Математичне моделювання
К. фіз.-мат. наук Готинчан І.З.
Чернівецький торговельно-економічний інститут
Київського
національного торговельно-економічного університету, Україна
ОДНА
ЗАДАЧА МОДЕЛЮВАННЯ ДИФУЗІЙНИХ ПРОЦЕСІВ В НЕОДНОРІДНИХ СЕРЕДОВИЩАХ З М’ЯКИМИ
МЕЖАМИ
Моделювання
процесів дифузії неоднорідних середовищах з м’якими межами методом гібридного
диференціального оператора Фур’є – Фур’є – Лежандра на декартовій вісі
приводить до побудови обмеженого в області ![]() розв’язку сепарат-ної
системи диференціальних рівнянь теплопровідності параболічного типу [1]
розв’язку сепарат-ної
системи диференціальних рівнянь теплопровідності параболічного типу [1]
![]()
![]() (1)
(1)
![]()
за початковими
умовами
![]() (2)
(2)
та умовами
спряження
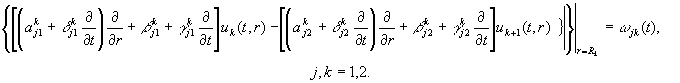 (3)
(3)
Ми
припустимо, що:
1) функції ![]() та
та ![]() є оригіналами за Лапласом стосовно
є оригіналами за Лапласом стосовно ![]() [2];
[2];
2) виконані
умови на коефіцієнти: ![]()
![]()
![]()
![]()
3)![]() - узагальнений диференціальний оператор Лежандра [3]:
- узагальнений диференціальний оператор Лежандра [3]:
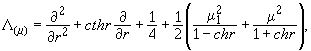
![]() ,
, ![]()
У зображенні
за Лапласом параболічній задачі (1)-(3) відповідає крайова задача: побудувати
на множині ![]() розв’язок сепаратної
системи диференціальних рівнянь Фур’є
та Лежандра для модифікованих функцій
розв’язок сепаратної
системи диференціальних рівнянь Фур’є
та Лежандра для модифікованих функцій
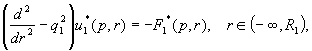
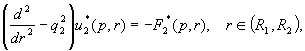 (4)
(4)
![]()
за умовами спряження
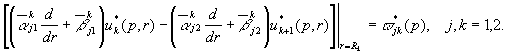 (5)
(5)
У рівностях
(4), (5) прийняті позначення:
![]()
![]()
![]() ;
;
![]()
![]()
![]()
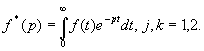
Фундаментальну
систему розв’язків для рівняння Лежандра ![]() утворюють
модифіковані приєднані функції Лежандра
утворюють
модифіковані приєднані функції Лежандра ![]() та
та ![]() [6], а фундаментальну систему розв’язків для рівняння Фур’є
[6], а фундаментальну систему розв’язків для рівняння Фур’є ![]() утворюють функції
утворюють функції ![]() та
та ![]() [4].
[4].
Наявність
фундаментальної системи розв’язків дозволяє побудувати розв’язок крайової
задачі (4), (5) методом функцій Коші [4, 5]:
![]()
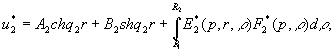 (6)
(6)
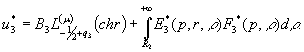
У рівностях
(6) беруть участь функції Коші ![]() [4,5]:
[4,5]:
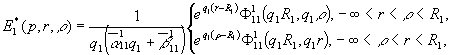 (7)
(7)
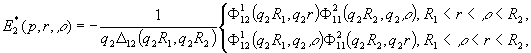 (8)
(8)
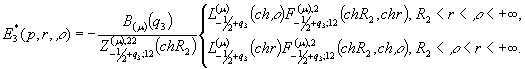 (9)
(9)
У рівностях
(7) – (9) беруть участь функції:
![]()
![]()
![]()
![]()
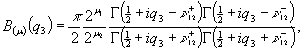
![]()
![]()
![]()
![]()
У мови
спряження (5) для визначення величин ![]() дають алгебраїчну
систему з чотирьох рівнянь:
дають алгебраїчну
систему з чотирьох рівнянь:
![]()
![]() (10)
(10)
У системі
(10) беруть участь символ Кронекера ![]() та функції
та функції
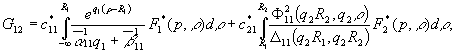
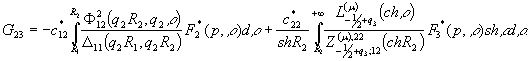
Визначимо
функції:
![]()
![]()
![]()
![]()
Припустимо,
що виконана умова однозначної розв’язності даної крайової задачі: для ![]() із
із ![]() де
де ![]() - абсциса збіжності інтеграла Лапласа, та
- абсциса збіжності інтеграла Лапласа, та ![]() визначник
алгебраїчної системи (10)
визначник
алгебраїчної системи (10)
![]()
![]() (11)
(11)
Введемо до
розгляду головні розв’язки крайової задачі (4),
(5):
1)
Породженні неоднорідністю умов спряження функцій Гріна
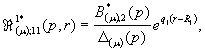
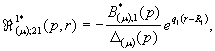
![]()
![]()
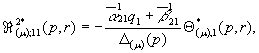
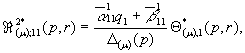 (12)
(12)
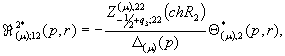
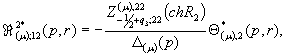
![]()
![]()
![]()
![]()
2)
породжені неоднорідністю системи (4) функції впливу

![]()
![]()
![]()
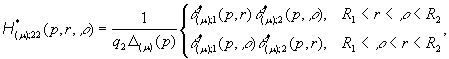 (13)
(13)
![]()
![]()
![]()
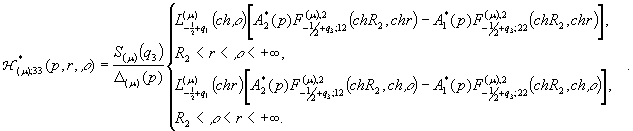
У результаті
однозначної розв’язності алгебраїчної системи (10) та підстановки обчислених
значень ![]() у формули (6)
отримуємо після низки елементарних перетворень єдиний розв’язок крайової задачі (4), (5):
у формули (6)
отримуємо після низки елементарних перетворень єдиний розв’язок крайової задачі (4), (5):
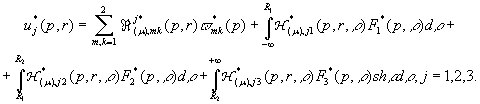 (14)
(14)
Повертаючись
у рівностях (14) до оригіналу, одержуємо єдиний розв’язок параболічної задачі
(1) –(3):
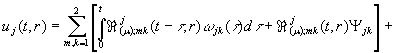
![]()
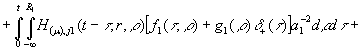 (15)
(15)
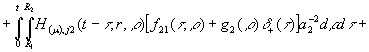
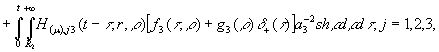
![]() - дельта-функція, зосереджена в точці
- дельта-функція, зосереджена в точці ![]()
У рівностях
(15) за означенням [5]
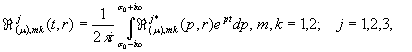 (16)
(16)
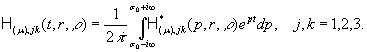 (17)
(17)
Особливими
точками функції Гріна ![]() та функцій впливу
та функцій впливу ![]() є точки розгалуження
є точки розгалуження ![]() та точка розгалуження
та точка розгалуження
![]() . Оскільки
. Оскільки ![]() то всі особливі точки
знаходяться на лівій піввісі
то всі особливі точки
знаходяться на лівій піввісі ![]() Це дає можливість
«сісти на уявну вісь» й одержати такі структури головних розв’язків даної
задачі теплопровідності:
Це дає можливість
«сісти на уявну вісь» й одержати такі структури головних розв’язків даної
задачі теплопровідності:
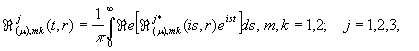 (18)
(18)
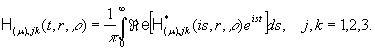 (19)
(19)
Тут ![]() означає дійсну частину виразу (…).
означає дійсну частину виразу (…).
Зауваження 1.
Можна вважати, що ![]() В протилежному
випадку переходимо до нових початкових умов
В протилежному
випадку переходимо до нових початкових умов![]()
![]()
![]()
![]() й вибираємо числа
й вибираємо числа ![]() та
та ![]() із алгебраїчної
системи
із алгебраїчної
системи
![]() (20)
(20)
Тут ![]() При виконанні умов на
коефіцієнти алгебраїчна система (20) завжди сумісна.
При виконанні умов на
коефіцієнти алгебраїчна система (20) завжди сумісна.
Зауваження 2.
Вибором параметрів, які беруть участь у формуванні даної задачі дифузії, можна
із загальних структур виділити безпосередньо в рамках даної моделі будь-який
частковий (практично важливий) випадок.
Література:
1.
Тихонов А.Н., Самарский
А.А. Уравнения математической физики. – М.: Наука, 1972. - 735 с.
2.
Лаврентьев М.А., Шабат
Б.В. Методы теории функций комплексного переменного. – М.: Наука, 1987. – 688
с.
3.
Конет І.М., Ленюк М.П. Інтегральні перетворення
типу Мелера - Фока. – Чернівці: Прут, 2002. – 248 с.
4.
Степанов В.В. Курс
дифференциальных уравнений. – М.: Физматгиз, 1959. – 468 с.
5. Шилов Г.Е. Математический анализ. Второй специальный курс. – М.: Наука, 1966. – 328 с.