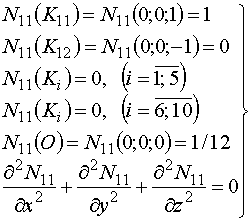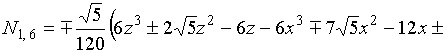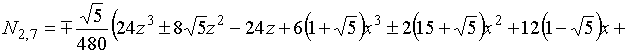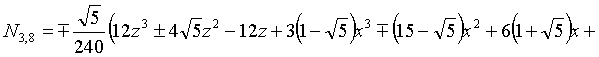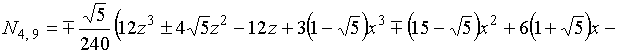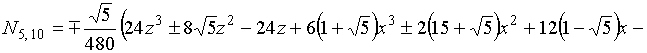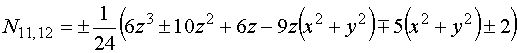Математика / 4. Прикладная математика

Зычкова Е.Э., Мотайло А.П., Тулученко Г.Я., Хомченко А.Н.

Херсонский национальный технический университет, Украина

Гармонический базис икосаэдра

на основе поверхностей вращения

Постановка проблемы. Распространение в природе и технике тел, имеющих форму правильного многогранника – икосаэдра, обуславливает целесообразность поиска возможностей улучшения качества интерполяции функций трех переменных по значениям, известным в вершинах этого тела, в конкретных задачах.

Применение метода линейных множителей для формирования набора базисных функций икосаэдра приводит к аномальному результату: функции, удовлетворяющие традиционному набору требований к базисным функциям, достигают единицы не только в своем узле, а и в точках, расположенных на ряде линий внутри икосаэдра. Таким образом, построенные по методу линейных множителей наборы функций не могут использоваться как базисы.

Анализ предшествующих публикаций. Вопросы построения базисных функций для интерполяции по узлам, расположенным в вершинах таких правильных многогранников как тетраэдр, куб и октаэдр, рассматриваются, в частности, в работах [1-4]. Влияние локальных характеристик базисов, ассоциированных с этими геометрическими телами, на качество интерполяции исследуется в работах [1, 4].

Цель публикации. Построить базис икосаэдра серендипового типа для трехмерной полиномиальной интерполяции в этом теле на основе гармонических поверхностей вращения третьего порядка и найти его локальные характеристики для прогноза аппроксимационных качеств.

Основная часть. Геометрический подход позволяет устранить указанный выше недостаток метода линейных множителей. Исходя из физического распределения равномерной массовой силы, естественно предположить, что в точках, равноудаленных от одноименного узла, базисная функция должна принимать равные значения. Геометрически это означает, что линиями уровня базисной функции должны быть поверхности вращения.

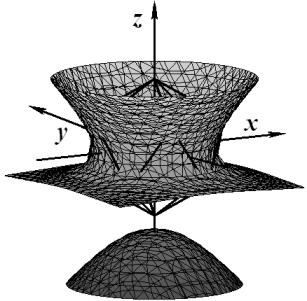
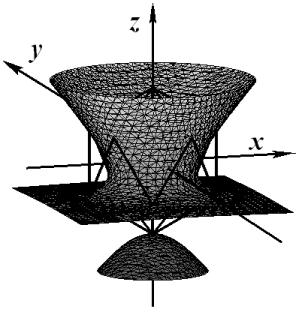
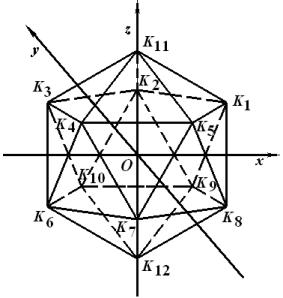
На примере базисной функции для узла (рис. 1) покажем принцип построения базисных функций икосаэдра на основе поверхностей вращения третьего порядка. Уравнение поверхности вращения в выбранной системе координат имеет вид:

,

(1)

где коэффициенты находятся из системы:

. Рис. 1. Икосаэдр

(2)

Первые четыре уравнения системы (2) отражают традиционные требования к базисной функции. Отметим, что две группы узлов и расположены на окружностях, поэтому подстановка в уравнение (1) координат этих узлов приводит к появлению двух линейно независимых уравнений (по одному для каждой группы).

Пятое уравнение обусловлено симметричной структурой икосаэдра. Шестое уравнение обеспечивает гармоничность базисной функции, что, как известно из литературы по вычислительной математике [1], улучшает аппроксимационные возможности базисных функций в ряде задач.

В результате решения системы (2) для функции (1) и выполнения серии преобразований (вращений) получаем гармонический базис икосаэдра на основе поверхности вращения третьего порядка:

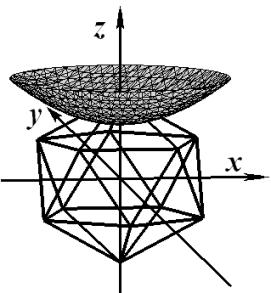
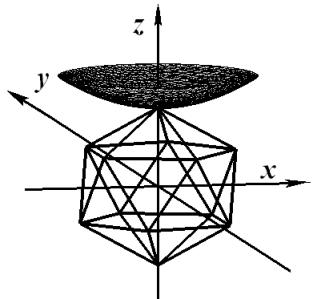
Графики поверхностей уровня для нескольких значений базисной функции представлены в табл. 1.

Для построенного базиса авторами вычислены такие его локальные характеристики как определитель матрицы Грама и число обусловленности матрицы Грама в норме метрики .

Из этих двух характеристик не зависит от величины объема тела только число обусловленности матрицы Грама в норме метрики .

Таблица 1

Поверхности уровня базисной функции

Сравнение по этой характеристике гармонических базисов тетраэдра [2], куба [2, 3] и октаэдра [4] проводится на рис. 2. В качестве гармонического базиса тетраэдра используется базис для линейной интерполяции в трехмерном симплексе. В качестве гармонического базиса куба используется базис для трилинейной интерполяции в этом теле.

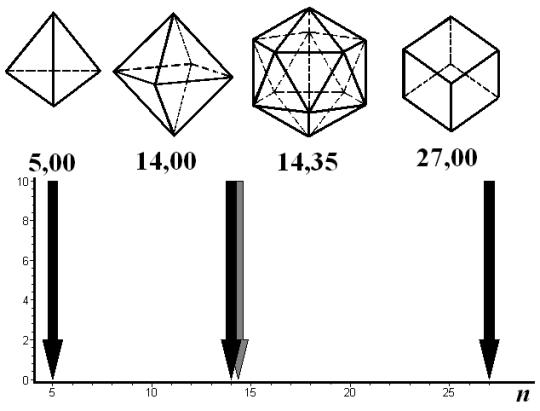
Рис. 2. Числа обусловленности матриц Грама в норме метрики
для гармонических базисов тел Платона

Выводы и перспективы дальнейших исследований. Полученное для гармонического базиса икосаэдра число обусловленности матрицы Грама в норме метрики позволяет предположить хорошие аппроксимационные свойства у этого базиса. Напомним, что лучшим считается базис, число обусловленности матрицы Грама которого ближе к единице.

Поэтому в дальнейшем авторы планируют провести тестирование построенного в данной статье базиса икосаэдра при решении серии практических задач.

Учитывая громоздкость полученных выражений для базисных функций, целесообразным является поиск других базисов икосаэдра с более простыми базисными функциями и удовлетворительными локальными характеристиками.

Литература

1. Юлдашев О.И. Гармонические базисные функции для конечных элементов высокого порядка аппроксимации [Электронный ресурс] / О.И. Юлдашев, М.Б. Юлдашева // Объединенный институт ядерных исследований. Лаборатория информационных технологий. Научный отчет 2006-2007. — Дубна: Объединенный институт ядерных исследований, 2007. — С. 317—320. — Режим доступа к отчету:

http://lit.jinr.ru/Reports/SC_report_06-07/pdfall/p317.pdf.

2. Сегерлинд Л. Применение метода конечных элементов / Л. Сегерлинд. — М.: Мир, 1979. — 392 с.

3. Пинежанинов Ф. Свойства базисных функций [Электронный ресурс] / Ф.Пинежанинов, П.Пинежанинов // Exponenta.ru — Режим доступа: http://www.nsu.ru/matlab/Exponenta_RU/soft/Mathemat/pinega/a2/a2.asp.htm

4. Мотайло А.П. Порівняльний аналіз лагранжевого та гармонічного базисів октаедра / А.П. Мотайло, А.Н. Хомченко, Г.Я. Тулученко // Праці Таврійського державного агротехнологічного університету. – Мелітополь, 2011. – Вип. 4. Прикладна геометрія, інженерна графіка. – Т. 51. – С. 64–70.