Мельник В.Н., Карачун В.В.
Национальный технический университет Украины «КПИ»
ВЫБОР АНАЛИТИЧЕСКОЙ АППРОКСИМАЦИИ ЛИНИИ МЕРИДИАНА
ОБОЛОЧКИ ВРАЩЕНИЯ
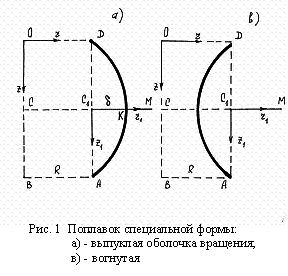 Рассмотрим
следующие типы оболочек вращения: выпуклая (рис.1, а) и вогнутая относительно
оси вращения (рис.1, в). В обоих случаях предполагается, что ОD=BA=R, а
кривая f(z),
образующая оболочку вращения, симметрична относительно прямой СМ, которая пересекает ось вращения в
середине (ОВ=l; OC=CB=
Рассмотрим
следующие типы оболочек вращения: выпуклая (рис.1, а) и вогнутая относительно
оси вращения (рис.1, в). В обоих случаях предполагается, что ОD=BA=R, а
кривая f(z),
образующая оболочку вращения, симметрична относительно прямой СМ, которая пересекает ось вращения в
середине (ОВ=l; OC=CB=![]() ). Считаем также, что
). Считаем также, что
![]() (1)
(1)
Рассмотрим систему координат C1z1r1 (рис.1). Связь между этой системой и
опорной Ozr определяется соотношениями –
r=r1+R; z=z1+![]() .
.
В
системе отсчета C1 z1 r1 форму оболочки (линию
меридиана) зададим выражением
![]() (2)
(2)
причем знак
«+» соответствует случаю рис. 1,
а, а
знак «-» -
случаю рис. 1 в.
Установим
класс кривых f1(z1), для которых выполняются
условия:
- ![]()
- ![]()
- функции
![]() строго выпуклые,
а функции
строго выпуклые,
а функции ![]() - строго
вогнутые;
- строго
вогнутые;
- точка с
координатой z1=0 является точкой экстремума для
функций ![]()
- функция
f1(z1)
считаем убывающей 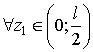 (рис. 1, а) и возрастающей при
(рис. 1, а) и возрастающей при 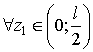 (рис.1, в).
(рис.1, в).
Рассмотрим
пример . Пусть
F1(z1)=a2-a0z12 , a2>0 ; a0>0 .
Очевидно, что f1(-z1)=f1(z1) .
Тогда, в соответствии с рис. 1, имеем:
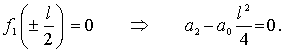
Отсюда определяем
коэффициент а2 –
![]()
С
учетом этого, можно записать:
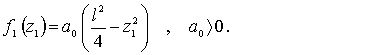 (3)
(3)
Обозначим величину подъема этой параболы
С1К в точке z1 = 0 через δ (рис. 1 , а) . Тогда
![]()
В этом
случае можно записать:
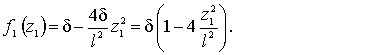 (4)
(4)
Представим уравнение линии меридиана оболочки в опорной системе
координат Ozr. Имеем:
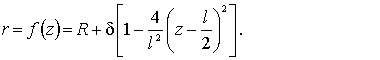 (5)
(5)
Или так:
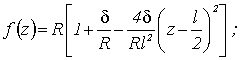 (6)
(6)
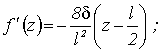 (7)
(7)
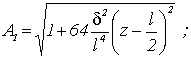 (8)
(8)
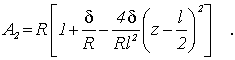 (9)
(9)
Рассмотрим другой пример. Пусть
![]()
Тогда:
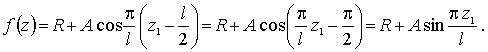
Как и ранее считаем, что ![]() и соответствует
максимальному отклонению линии меридиана от вертикальной прямой r = R. Тогда,
и соответствует
максимальному отклонению линии меридиана от вертикальной прямой r = R. Тогда,
![]() (10)
(10)
Отсюда следует,
что
![]()
и тем
самым, постоянные Ламе определяются соотношениями-
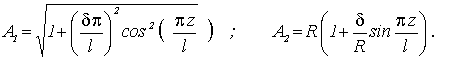 (11)
(11)
Остается вычислить радиусы кривизны.