Сурнева О.Б.
Некоторые решения нелинейного
параболического уравнения
с тремя независимыми переменными
СКФУ г.Ставрополь, Россия
Лемма
1. Уравнение на функцию ![]() [1]
[1]
![]() (1)
(1)
эквивалентна операторному уравнению Лакса ![]() с операторами L и А
с операторами L и А
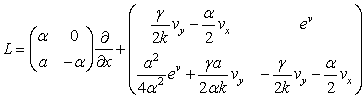 ,
,
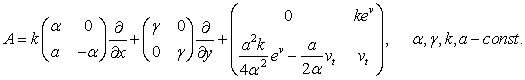
1. Сужение пространства к двумерному случаю
Лемма
2.
Уравнение (1), при ![]() ,
, ![]() сводится к гиперболическому
квазилинейному уравнению [2]
сводится к гиперболическому
квазилинейному уравнению [2]
![]() , (2а)
, (2а)
с помощью замены: ![]() ,
, ![]() ,
, ![]() ,
, 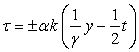 .
.
Лемма
3. Уравнение
(1), при ![]() ,
, ![]() сводится к
эллиптическому квазилинейному уравнению на комплекснозначную функцию
сводится к
эллиптическому квазилинейному уравнению на комплекснозначную функцию
![]() , (2б)
, (2б)
с помощью замены: ![]() ,
, ![]() ,
, ![]() ,
, 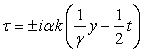 .
.
2. Точные решения
ТЕОРЕМА
1.
Уравнение (2а), при ![]() ,
, ![]() имеет частное решение
вида:
имеет частное решение
вида: 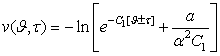 , где
, где ![]() – произвольная постоянная.
– произвольная постоянная.
ТЕОРЕМА
2.
Уравнение (1), имеет частное решение вида: 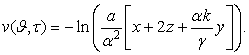
ТЕОРЕМА 3. Уравнение (1), при ![]() ,
, ![]() сводится к параболическому
квазилинейному уравнению вида
сводится к параболическому
квазилинейному уравнению вида
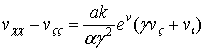 , (5)
, (5)
где ![]() - неизвестная функция
трех переменных:
- неизвестная функция
трех переменных: ![]() ,
, ![]() ,
, 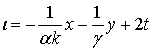 .
.
ТЕОРЕМА 4. Уравнение (5), имеет решение вида
![]() ,
,
где ![]() – произвольные
функции.
– произвольные
функции.
ТЕОРЕМА 5. Уравнение (5), имеет следующие частные
решения:
![]() ,
,
![]() ,
,
где ![]() -произвольные
параметры.
-произвольные
параметры.
Доказательства
поводятся простой проверкой.
Выполним в уравнении
(5) преобразования позволяющие избавиться от показательной функции. Положим ![]() , тогда (5) примет вид
, тогда (5) примет вид
![]() .
(6)
.
(6)
Проведем анализ, позволяющий сказать, существует
автомодельное решение или нет. Автомодельные
решения существуют, если растяжение независимых и зависимых переменных по
правилу ![]() , где постоянная
, где постоянная ![]() , при соответствующем выборе
, при соответствующем выборе ![]() эквивалентно тождественному
преобразованию, т. е. исходное уравнение переходит само в себя
эквивалентно тождественному
преобразованию, т. е. исходное уравнение переходит само в себя
![]() ,
,
поэтому должны
выполняться равенства ![]() , которые дают
, которые дают ![]() . Это означает что все переменные уравнения (6) имеют
одинаковый вес. Кроме этого все слагаемые исследуемого уравнения (6) имеют
одинаковый суммарный вес равный 4. Определим, в каком соотношении необходимо
брать автомодельную связь между независимыми переменными, положим
. Это означает что все переменные уравнения (6) имеют
одинаковый вес. Кроме этого все слагаемые исследуемого уравнения (6) имеют
одинаковый суммарный вес равный 4. Определим, в каком соотношении необходимо
брать автомодельную связь между независимыми переменными, положим ![]() , где
, где ![]() - произвольные
параметры, тогда (6) примет вид
- произвольные
параметры, тогда (6) примет вид
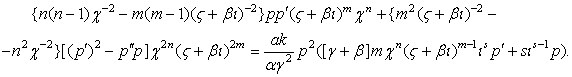 (7)
(7)
Полная замена на
переменную ![]() в полученном
равенстве возможна если
в полученном
равенстве возможна если ![]() ,
, ![]() кроме этого для
сокращения необходимо, чтобы коэффициенты
кроме этого для
сокращения необходимо, чтобы коэффициенты
![]() и
и ![]() были пропорциональны,
тогда получим
были пропорциональны,
тогда получим
![]() . (8)
. (8)
где ![]() - коэффициент
пропорциональности. В результате наложенных
условий равенство (7) преобразуется к виду
- коэффициент
пропорциональности. В результате наложенных
условий равенство (7) преобразуется к виду
![]() .
.
После двукратного
интегрирования функция примет вид
![]() .
.
Возвращаясь к старой
функции, получим решение
![]() . (9)
. (9)
ТЕОРЕМА 7. Уравнение (5), имеет частное решение (9),
где ![]() – произвольные
постоянные.
– произвольные
постоянные.
Литератера:
1. Сурнева О.Б. 2+1- мерное
дифференциальное уравнение в частных производных обладающее парой Лакса//Materiály VIII mezinárodní vědecko – praktická
Konference «Zprávy vědecké ideje –
2012». Díl
21 Matematika. Fyzika. Moderní informační technologie.
Výstavba a architektura: Praha. Publishing House «Education and Science» s.r.o. 2012.
3-5.
2. Редькина Т.В. Возможность
построения солитонных 1+1 и 2+1 - мерных уравнений, имеющих общую задачу
рассеяния// Вестник СГУ, № 43. Ставрополь,
2005, с. 47-52.