К. ф.-м. н. Редькина Т.В.
Операторы преобразования
специального вида
СКФУ г.Ставрополь, Россия
Рассмотрим дифференциальные
операторы М и В, и образующие пару Лакса ![]() , (1)
, (1)
если коммутатор ![]() и производная
и производная ![]() являются операторами
умножения на некоторые функции, где
являются операторами
умножения на некоторые функции, где
![]()
![]() , (2)
, (2)
«¾» над буквой обозначает комплексное сопряжение, а L
– оператор, зависящий от комплексной
функции ![]() и имеет вид оператора Шредингера.
и имеет вид оператора Шредингера.
ТЕОРЕМА 1. Если коэффициенты полиномов
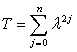 ,
, 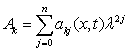 ,
, 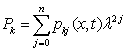 ,
, 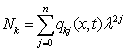 ,
, ![]() ,
,
где п – фиксированное натуральное число (пÎN), удовлетворяют следующим рекуррентным формулам: ![]() ,
, ![]()
![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]()
j=0,1,…,n, то оператор
![]() вида:
вида:
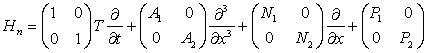 , (3)
, (3)
преобразует решения уравнения ![]() в функции
в функции ![]() , удовлетворяющие уравнениям
, удовлетворяющие уравнениям
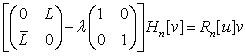 ,
,
где 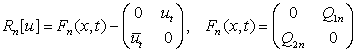 - матрица, не
зависящая от l.
- матрица, не
зависящая от l.
СЛЕДСТВИЕ 1. Для того чтобы
функция ![]() удовлетворяла уравнению
удовлетворяла уравнению
![]() , необходимо и достаточно, чтобы операторы
, необходимо и достаточно, чтобы операторы ![]() преобразовывали
решения уравнения
преобразовывали
решения уравнения ![]() в решение этого же уравнения.
в решение этого же уравнения.
СЛЕДСТВИЕ 2. Для оператора М вида (2) существует оператор
В вида
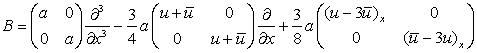 , (4)
, (4)
СЛЕДСТВИЕ 3. Оператор ![]() преобразует
решение уравнения
преобразует
решение уравнения ![]() в функции удовлетворяющие неоднородному
уравнению
в функции удовлетворяющие неоднородному
уравнению
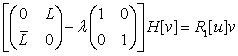 ,
,
где
операторы имеют следующий вид: В – (4), L – (2), а
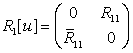 ,
, ![]() . (5)
. (5)
При ![]() (5) дает ранее
полученную комплексификацию уравнения Кортевега – де Вриза [1]
(5) дает ранее
полученную комплексификацию уравнения Кортевега – де Вриза [1]
![]() .
.
Операторы преобразования высшего порядка
ТЕОРЕМА 2.
Операторы ![]() , n =1, 2,… вида
, n =1, 2,… вида
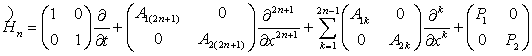 , (6)
, (6)
где п ≥ 2 – фиксированное натуральное число (пÎN), преобразуют
решения уравнения ![]() в функции
в функции
![]() , удовлетворяющие уравнениям
, удовлетворяющие уравнениям
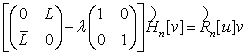 ,
,
где 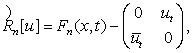
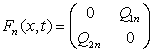 - матрица, не
зависящая от
- матрица, не
зависящая от ![]() .
.
СЛЕДСТВИЕ 2. Операторное
уравнение Лакса (1), где М имеет вид (2), а
В – семейство дифференциальных операторов записанных в симметричном виде
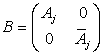 ,
, 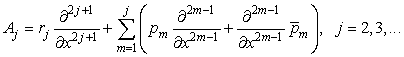 (7)
(7)
где ![]() - действительное
постоянное число,
- действительное
постоянное число, ![]() - функции от комплексной переменной
- функции от комплексной переменной ![]() и ее производным по переменной х порождает семейство комплексификации высших
уравнений Кортевега – де Вриза.
и ее производным по переменной х порождает семейство комплексификации высших
уравнений Кортевега – де Вриза.
СЛЕДСТВИЕ 3. Нелинейное уравнение на комплексную функцию ![]()
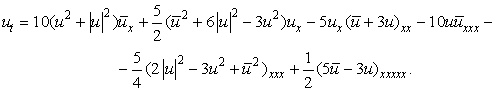 (8)
(8)
имеет
представление Лакса (1) с операторами М (2), где
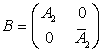 ,
, 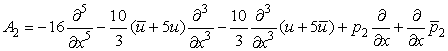 ,
,
где ![]() , и является комплексификацией
второго уравнения иерархии Кортевега – де Вриза .
, и является комплексификацией
второго уравнения иерархии Кортевега – де Вриза .
ТЕОРЕМА 3. Нелинейная система уравнений
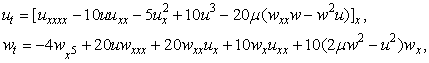
имеет представление Лакса (1) с операторами М и В вида
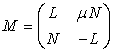 ,
, 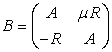 ,
,
где L - оператор Шредингера, а остальные
операторы имеют вид
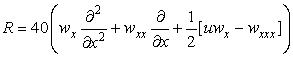 ,
, ![]() ,
,
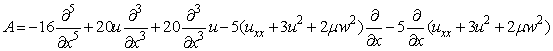 ,
,
где ![]() - произвольные
действительные функции,
- произвольные
действительные функции, ![]() - произвольный
параметр.
- произвольный
параметр.
Литература:
1.
Редькина Т.В.
Некоторые свойства комплексификации уравнения Кортевега - де Вриза. Известия АН
СССР. Сер. матем. Т.55, № 6, 1991, с.1300-1311.