УДК 517.
957
О СУЩЕСТВОВАНИИ РЕШЕНИЙ НЕЛИНЕЙНЫХ НАГРУЖЕННЫХ ВЫРОЖДАЮЩИХСЯ УРАВНЕНИЙ.
Кандидат физико – математических наук Рахимова Гульжан Кадырхановна
1. Введение и формулировка результатов.
Общая
теория краевых задач для вырождающихся эллиптических уравнений в наиболее
важных направлениях считается
завершенной. Весьма исчерпывающая библиография содержится в работах С.М.
Никольского [1], П.И. Лизоркина и С.М. Никольского [2], М.М. Смирнова [3], А.В. Бицадзе [4], М.И.
Вишика и В.В. Грушина [5], В.П.Глушко
[6], Т.Ш.Кальменова и М. Отелбаева [7], М.Б.Муратбекова [8-9] и других авторов.
В настоящей
работе исследуется дифференциальный оператор
неклассического типа. Здесь полученные результаты дополняют работы выше
указанных авторов. Причем в отличие от вышеуказанных исследований в данной
работе охватываются случай нечетного порядка.
В этой
работе будем изучать задачу:
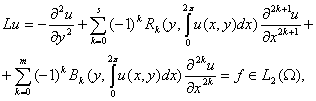 (1)
(1)
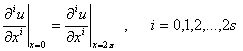 (2)
(2)
![]() (3)
(3)
где ![]() .
.
В дальнейшем считаем, что функции ![]() ,
, ![]() кусочно-непрерывны и
ограничены по обоим аргументам и удовлетворяют следующие условия:
кусочно-непрерывны и
ограничены по обоим аргументам и удовлетворяют следующие условия:
![]()
![]() ,
, ![]() ,
,
![]() ,
, ![]()
![]()
![]() и при каждом
и при каждом ![]() не убывают на отрезке
[0,1].
не убывают на отрезке
[0,1]. ![]() и
при каждом
и
при каждом ![]() не убывают на отрезке
[0,1].
не убывают на отрезке
[0,1].
![]()
![]() и при всех
и при всех ![]() ;
;
![]() и при всех
и при всех ![]() .
.
Теорема 1. Пусть
выполнены условия ![]() -
-![]() . Тогда
существует решение задачи (1)-(3)
. Тогда
существует решение задачи (1)-(3)
такое, что
![]() , (4)
, (4)
где С>0 – постоянное число.
Здесь
![]() - норма пространства
- норма пространства ![]() .
.
2. О свойствах периодических решений для одного класса
нелинейных вырождающихся уравнений.
Рассмотрим
задачу:
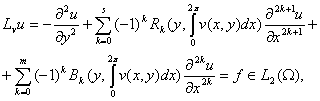 (2.1)
(2.1)
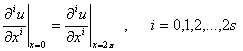 , (2.2)
, (2.2)
![]() .
(2.3)
.
(2.3)
Лемма
2.1. Пусть ![]() и выполнено условие
и выполнено условие![]() . Тогда для любой
правой части f из
. Тогда для любой
правой части f из ![]() существует, притом единственное решение задачи (3.1)-(3.3),
такое, что
существует, притом единственное решение задачи (3.1)-(3.3),
такое, что
![]() , (2.4)
, (2.4)
где C>0 не зависит от u, v.
Доказательство. Положим
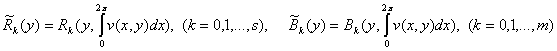
Тогда (2.1)-(2.3)
сводится к задаче (1)-(3), где функции ![]() заменены, соответственно,
на
заменены, соответственно,
на ![]() . При этом согласно условию
. При этом согласно условию ![]() для
для ![]() выполняются все
условия теоремы 1 [8], откуда вытекает
утверждение доказываемой леммы. Таким образом, задача (2.1)-(2.3) имеет единственное решение
выполняются все
условия теоремы 1 [8], откуда вытекает
утверждение доказываемой леммы. Таким образом, задача (2.1)-(2.3) имеет единственное решение ![]() удовлетворяющее
оценку (2.4). Очевидно, если
удовлетворяющее
оценку (2.4). Очевидно, если ![]() , то
, то ![]() . Более того, поскольку
. Более того, поскольку ![]() – решение задачи (2.1)-(2.3), для произвольной функции
– решение задачи (2.1)-(2.3), для произвольной функции ![]() имеем
имеем ![]() . Поэтому, существование решения краевой задачи (1)-(3)
эквивалентно существованию неподвижной точки оператор
. Поэтому, существование решения краевой задачи (1)-(3)
эквивалентно существованию неподвижной точки оператор ![]() в пространстве
в пространстве ![]() т.е. существование
функции
т.е. существование
функции ![]() такой, что
такой, что ![]() . При этом
. При этом ![]() , поскольку
, поскольку ![]()
Следовательно,
задача (1)-(3) имеет решение, если оператор ![]() имеет неподвижную
точку. С этой целью применяем известный принцип Шаудера.
имеет неподвижную
точку. С этой целью применяем известный принцип Шаудера.
Пусть ![]() – шар в пространстве
– шар в пространстве ![]() и А- произвольное
положительное число.
и А- произвольное
положительное число.
Лемма 2.2. Пусть выполнено условие ![]() . Тогда оператор
. Тогда оператор ![]() отображает множество
отображает множество ![]() в себя.
в себя.
Доказательство. Доказательство
леммы следует из теоремы 1[8] и леммы 2.1., если в качестве А взять число ![]() из оценки (2.4).
Пусть
из оценки (2.4).
Пусть ![]() – прообраз шара
– прообраз шара ![]() .
.
Лемма
2.3. Пусть выполнено условие ![]() . Тогда для любой функции u из М
справедливо неравенство
. Тогда для любой функции u из М
справедливо неравенство
![]()
где C>0 –
постоянное число.
Доказательство. Доказательство
леммы следует из леммы 3.1.
Покажем,
что в условиях теоремы 1.1 оператор ![]() является вполне непрерывным в
является вполне непрерывным в ![]() . Для этого достаточно показать компактность множества М в
пространстве
. Для этого достаточно показать компактность множества М в
пространстве ![]() и непрерывность
оператора
и непрерывность
оператора ![]() . Рассмотрим множества:
. Рассмотрим множества:
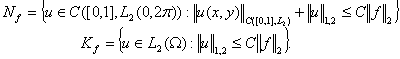
Пользуясь леммой 2.3 получим соотношения
![]() (2.5)
(2.5)
Пусть ![]() - множество, состоящее из функции вида
- множество, состоящее из функции вида
![]()
где ![]() , а
, а ![]() – усредняющее ядро.
Известно, что
– усредняющее ядро.
Известно, что
1)
функция ![]() - бесконечно дифференцируемая;
- бесконечно дифференцируемая;
2)
![]() при
при ![]() при
при ![]() ;
;
3)
![]()
Лемма
2. 4. Множество ![]() компактно в
пространстве
компактно в
пространстве ![]() .
.
Доказательство. Пусть ![]() – множество,
состоящее из средних функции
– множество,
состоящее из средних функции ![]() , построенных по функциям
, построенных по функциям ![]() , принадлежащим множеству
, принадлежащим множеству ![]() . Из (2.5), непосредственно
вычисляя, имеем, что
. Из (2.5), непосредственно
вычисляя, имеем, что
![]() (2.6)
(2.6)
При любом фиксированном ![]() множество
множество ![]() компактно в
компактно в ![]() . Тогда согласно (2.6) множество
. Тогда согласно (2.6) множество ![]() компактно в
компактно в ![]() . Лемма 2.4 доказана.
. Лемма 2.4 доказана.
Лемма 2.5. Если
выполнено условие ![]() , то множество М компактно в пространстве
, то множество М компактно в пространстве ![]() .
.
Доказательство. Множество ![]() компактно в
компактно в ![]() согласно лемме 3.4. Отсюда следует, что
согласно лемме 3.4. Отсюда следует, что ![]() компактно в
компактно в ![]() . Доказательство последнего утверждения вытекает из следствия
теоремы 2 из [8 ст.
89].
. Доказательство последнего утверждения вытекает из следствия
теоремы 2 из [8 ст.
89].
Поскольку ![]() , то множество М компактно в
, то множество М компактно в ![]() . Лемма доказана. Осталось проверить непрерывность оператора
. Лемма доказана. Осталось проверить непрерывность оператора ![]() .
.
Лемма 2.6. Пусть выполнено условие![]() . Тогда оператор
. Тогда оператор ![]() непрерывен.
непрерывен.
Доказательство. Пусть
последовательность ![]() и элемент
и элемент ![]() из множества
из множества ![]() , такие, что
, такие, что ![]() в норме
пространства
в норме
пространства ![]() .
.
Положим ![]() и
и
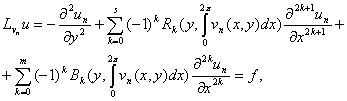
где ![]() - фиксированный элемент в
- фиксированный элемент в ![]() . Тогда
. Тогда
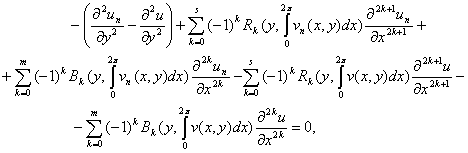
или
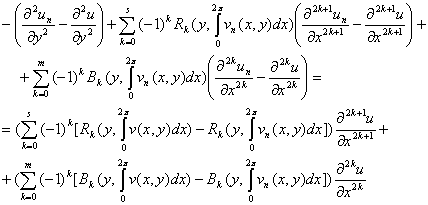 (2.7)
(2.7)
Левая часть последнего равенства имеет вид:
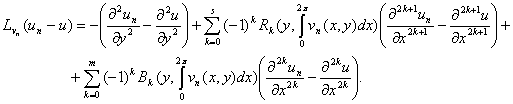
Отсюда и из (2.7) находим:
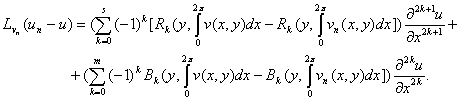
По предположению, коэффициенты оператора ![]() удовлетворяют
условиям теоремы 1[8]., следовательно
существует обратный оператор
удовлетворяют
условиям теоремы 1[8]., следовательно
существует обратный оператор
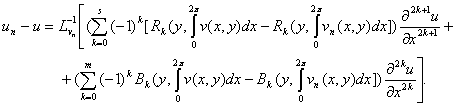
Отсюда
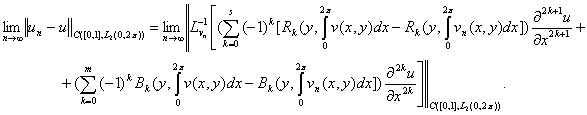
Пользуясь теореммой 1 и 2 [8] имеем:
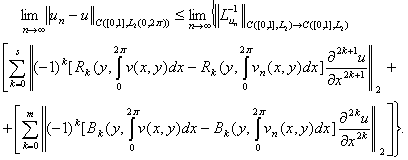 (2.8)
(2.8)
Из теоремы 2.1. также следует, что
![]() (2.9)
(2.9)
для всех ![]() и
и ![]() . А из (5) [8] получим оценки:
. А из (5) [8] получим оценки:
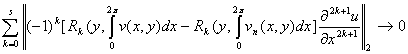 , при
, при ![]() (2.10)
(2.10)
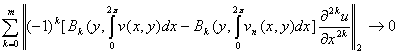 , при
, при ![]() (2.11)
(2.11)
Учитывая оценки (2.9)-(2.11), из неравенства (2.8) имеем:
![]() (2.12)
(2.12)
Здесь мы воспользовались тем, что ![]() при
при ![]()
Неравенство (2.12) доказывает лемму.
Доказательство теоремы 1. Согласно
леммам 2.5-2.6
оператор ![]() вполне непрерывен и переводит шар
вполне непрерывен и переводит шар ![]() в себя. Тогда согласно принципу
Шаудера оператор
в себя. Тогда согласно принципу
Шаудера оператор ![]() при фиксированном
при фиксированном ![]() имеет неподвижную точку в
имеет неподвижную точку в ![]() . Это означает, что задачи (1)-(3) для любой правой части
. Это означает, что задачи (1)-(3) для любой правой части ![]() имеет решение
имеет решение ![]() , принадлежащее шару
, принадлежащее шару ![]() , причем верна оценка:
, причем верна оценка:
![]()
Теорема доказана.
Список литературы
1.
Никольский С.М. Вариационная
проблема для уравнения эллиптического типа вырождением на границе // Труды Мат.
Ин-та АН СССР. - 1979. - Т. 150, - С.212-238.
2.
Лизоркин П.И., Никольский С.М.Эллиптические уравнения с
вырождением. Дифференциальные свойства решений // Доклад АН СССР. -
1981. -Т.257. - №1. - С.42-45.
3.
Смирнов М.М. Вырождающиеся
эллиптические и гиперболические уравнения. -
М.: – 1966. -С.292.
4.
Бицадзе А.В. Уравнения
смешанного типа. М.: - 1970. – С.164.
5.
Вишик М.И., Грушин В.В.
Краевые задачи для эллиптических уравнений вырождающихся на границе области //
Матем. сб. – 1969. –Т.80. – №4. – С.455-491.
6.
Глушко В.П.
Коэрцитивность в ![]() общих граничных
задачах для вырождающегося эллиптического уравнения второго порядка //
Функциональный анализ и его приложения. – 1968. – С.87-88.
общих граничных
задачах для вырождающегося эллиптического уравнения второго порядка //
Функциональный анализ и его приложения. – 1968. – С.87-88.
7.
Кальменов Т.Ш., Отелбаев
М. О гладкости решений одного класса вырождающихся эллиптических уравнений //
Дифференциальные уравнения. –1977– Т.13. – № 7. – С.1244-1255.
8.
Муратбеков
М.Б.Коэрцитивные оценки для одного дифференциального оператора высшего порядка
// Дифференциальные уравнения. –1981– Т.17. – № 5. – С.893-901.
9.
Муратбеков М.Б. О гладкости решений одного класса неравномерно
вырождающихся эллиптических уравнений // Известия АН Каз ССР. Сер.физ-мат. - 1981. - №5. - С.71-73.