Ганцева Е.А., Каладзе В.А.

ФУНКЦИОНАЛЬНЫЕ СЛОИ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ,
ПРЕДНАЗНАЧЕННЫЕ ДЛЯ ОПИСАНИЯ ДИНАМИКИ

В современных исследованиях активно развивается и совершенствуется архитектура искусственных нейронных сетей, представляющих собой вычислительный комплекс, обоснование конфигурации и процедур которого выстроено на аналогии с биологическими нейронными сетями, расширяется и область их применения. Но внедрение в структуру сетей вычислительных методов связано с эвристическим подходом и используется в основном для обучения параметров сети.

В работе рассматривается возможность модификации первых скрытых слоёв нейронной сети [1] при решении задач численного моделирования систем, обладающих динамикой. Реализация такого подхода облегчается тем, что структура численного моделирования динамики достаточно просто формируется на основе закономерностей конструирования нейронов и их взаимосвязей в скрытых слоях нейросети.

Для обеспечения адекватного описания эволюционного поведения моделируемого объекта вычислительными методами, внедрёнными в нейронную сеть, требуется априорная информация о порядке и параметрах динамической системы. Если такая информация отсутствует, то на рекуррентной основе проводится обучение параметров функционального слоя сети, что позволяет в ходе численного моделирования адаптироваться к параметрам динамической системы в соответствии с выбранным критерием. Настройка характеристик сети, ответственных за порядок динамики системы, обеспечивается формированием дополнительных связей между слоями. Необходимые процедуры адаптации будут описаны в следующей работе.

Рассмотрим задачу моделирования динамической линейной системы n-го порядка. Воспользуемся её математической постановкой, для решения которой применим классические вычислительные методы.

Пусть задана система n дифференциальных уравнений 1-го порядка

dY(t) = A Y(x) dt, при x(0) = x₀, y(x₀) = y₀,

где А – квадратная матрица постоянных коэффициентов системы размера n×n;

Y – n-мерный вектор оцениваемой функции.

Решение такой системы можно представить в соответствии со схемой Рунге-Кутта первого порядка (или что тоже – метода Эйлера) в виде матричного уравнения

Y_t+1 = Y_t + hAY_t = (E + hA)Y_t = B_t Y_t,

где Е – единичная матрица размера n×n; B – матрица коэффициентов разложения Тейлора; h – приращение аргумента.

Проведём синтез динамического слоя на примере динамики второго порядка. Матричное уравнение для n = 2 покомпонентно представимо в виде системы двух рекуррентных уравнений

y_1t+1 = b₁₁y_1t + b₁₂y_2t = (1 + ha₁₁)y_1t + ha₁₂y_2t,
y_2t+1 = b₂₁y_1t + b₂₂y_2t = ha₂₁y_1t + (1 + ha₂₂)y_2t.

Покомпонентное представление матричного уравнения позволяет сформировать структуру соответствующего слоя нейросети с учётом начальных условий для решения исходной системы уравнений.

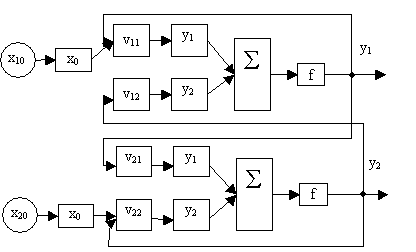
Схема реализации решения системы дифференциальных уравнений

Схема рекуррентной взаимосвязи двух нейронов, показанная на рисунке, реализует численное решение указанной системы двух уравнений. Входные сигналы x₁₀ и x₂₀ сообщают нейронам слоя первоначальное возбуждение и одновременно являются начальными условиями для решения исходной системы уравнений.

Несмотря на то, что функция активации у обоих нейронов линейная, существенные отличия в конфигурации этого слоя от остальных скрытых слоёв нейронной сети не позволит ей «схлопнуться» до одного слоя в условиях линейной активации соседних слоёв.

Распространение указанного способа реализации в нейронной сети вычислительного метода численного моделирования динамической линейной системы n-го порядка осуществляется теми же приёмами.

В реальных задачах входная информация содержит выборки данных с искажёнными результатами наблюдений за состоянием исследуемой системы. В этой связи, следующей задачей численного моделирования, решаемой нейросетевыми методами, можно считать задачу фильтрации статистических помех, когда скрытый слой формируется для выделения полезного сигнала из статистической последовательности входных данных. В качестве вычислительной процедуры для этой цели может быть использован каскадный фильтр с экспоненциальным эффективным преобразованием [2].

Использованные литературные источники

1. Ганцева Е.А. О функциональном использовании слоёв и направленных алгоритмах обучения ИНС// Труды второй всеросс. конф. Критические технологии вычислительных и информационных систем. Воронеж: МИКТ, 2013. С. 37-47.

2. Каладзе В.А. Каскадный фильтр динамической модели и его экспоненциальное преобразование Вестник ВГТУ. Том 6, № 12. – Воронеж: ВГТУ, 2010. С.147-151.