К.ф-м.н. Макаричев А.В., Кудь А.А., Щукин А.Б.

Харьковский национальный автомобильно-дорожный университет

Национальный аэрокосмический университет «ХАИ»

О ВРЕМЕНИ ОБНАРУЖЕНИЯ АЛЬТЕРНИРУЮЩЕГО ПРОЦЕССА В РЕГУЛЯРНОМ И ПРОСТЕЙШЕМ ПОТОКАХ ЕГО ИДЕНТИФИКАЦИИ

В процессе использования новой техники возникают альтернирующие процессы. Моменты их идентификации представляют собой поток однородных событий [1]. В некоторый момент времени возникает скачок вверх альтернирующего процесса, продолжительность пребывания которого в этом состоянии (продолжительность сигнала) есть неотрицательная случайная величина с функцией распределения . Нас интересует вероятностное распределение времени от начала сигнала до момента его обнаружения при условии, что он обнаружен. Рассмотрим два важных с практической точки зрения случая.

1. Стационарный регулярный поток моментов идентификации альтернирующего процесса.

Первый момент начала потока идентификации имеет равномерное распределение на отрезке . Время между соседними моментами идентификации сигналов постоянно и равно . Легко видеть, что вероятность того, что возникший сигнал будет не обнаружен, равна

,

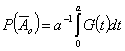А вероятность обнаружения возникшего сигнала определяется по формуле

,

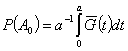где .

Функция распределения случайной величины - времени от начала сигнала до момента его обнаружения при условии, что сигнал будет обнаружен, равна

, .

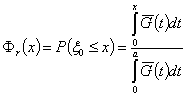Условное математическое ожидание времени от момента начала сигнала до момента его обнаружения при условии, что он обнаружен, равно

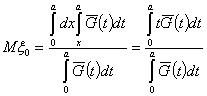
Моменты случайной величины - условного времени от момента начала сигнала до момента его обнаружения при условии, что он обнаружен, найдем в виде

, .

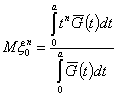А её дисперсия равна

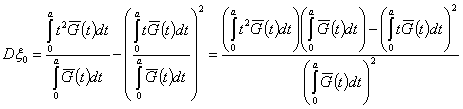
2. Простейший поток моментов обнаружения сигналов.

Предположим, что время между соседними моментами идентификации имеет показательное распределение с параметром . В этом случае вероятность не обнаружения возникшего сигнала (он длится между соседними моментами его идентификации) в силу отсутствия последействия для показательного распределения равна

А вероятность обнаружения возникшего сигнала определяется по формуле

Функция распределения случайной величины - времени от начала сигнала до момента его обнаружения при условии, что сигнал будет обнаружен, равна

.

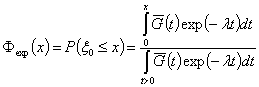Условное математическое ожидание времени от момента начала сигнала до момента его обнаружения при условии, что он обнаружен, равно

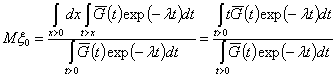
Моменты этой случайной величины могут быть найдены в виде

, .

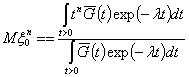Второй центральный момент (дисперсия) случайной величины определяется по формуле

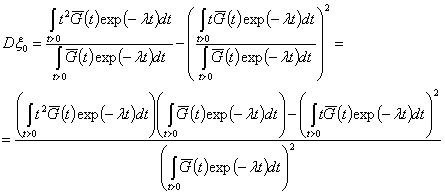
Пример. Экспоненциальное распределение времени продолжительности сигнала.

Предположим, что

, , .

Нетрудно видеть, что условная вероятность того, что время от момента начала сигнала до момента его обнаружения при условии, что сигнал обнаружен, равна

, .

Таким образом, в случае экспоненциального распределения времени продолжительности сигнала в простейшем потоке его идентификации условное распределение времени от момента начала сигнала до момента его обнаружения при условии, что он обнаружен, также является экспоненциальным с параметром равным сумме параметров: показательного распределения времени продолжительности сигнала и параметра простейшего потока его идентификации.

Литература.

1. B.V.GNEDENKO AND I.N.KOVALENKO, Introduction to Queueing Theory, Program for Scientific Translations, Jerusalem, 1968.

2. Ширяев А.Н. Вероятность, М.: Наука, 1980, 576 c.