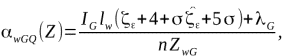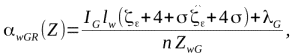к.т.н. Крючин О.В.

Тамбовский государственный университет им. Г.Р. Державина, Россия

Аналитическая модель параллельных информационных процессов обучения искусственных нейронных сетей использующих градиентные методы

Как показано в работах [1-3], при параллельной реализации градиентных методов обучения искусственных нейронных сетей (ИНС) алгоритм на управляющем элементе информационного ресурса (ИР-элементе) следующий: 1) формирование структуры ИНС (включая инициализацию весовых коэффициентов начальными значениями); 2) передача структуры ИНС на все используемые ИР-элементы; вычисление весов ; 3) получение с ненулевых ИР-элементов; 4) формирование вектора и вычисление значения невязки ; проверка необходимости остановки; 5) отправка команды остановки на все неведущие ИР-элементы; 6) если обучение не закончено, то отправка весовых коэффициентов на все ИР-элементы и переход к пункту 3.

Ненулевые ИР-элементы используют другой порядок выполнения информационного процесса: 1) получение структуры ИНС с ведущего ИР-элемента; 2) вычисление значений элементов вектора ; 3) отправка вектора на ведущий ИР-элемент; 4) получение команды окончания обучения; 5) если обучение не окончено, то получение полного вектора весовых коэффициентов и переход к пункту 2 [3].

Исходя из того, что для вычисления одного элемента градиента требуется () мультипликативная и () аддитивных операций (где , — число мультипликативных и аддитивных операций, необходимых для вычисления значения невязки) [1-3], можно вывести, что для одной итерации градиентных методов, требуется количество операций, равное приведенному в табл. 1.

Таблица 1. К-во операций одной итерации градиентных методов.

Метод	мультипликативных	аддитивных
Наискорейшего спуска
QuickProp
RPROP

Каждая параллельная итерация информационного процесса состоит из нескольких этапов: 1) рассылка ведущим ИР-элементом вектора весовых коэффициентов ; 2) вычисление элементов своей части градиента и весовых коэффициентов; 3) передача на ведущий ИР-элемент новых значений весовых коэффициентов [1].

Первый этап требует у ведущего ИР-элемента ( мультипликативных и аддитивных операций, а у -го неведущего () — соответственно ( для передачи данных, для ожидания передачи). Количества операций, необходимых для второго этапа приведены в табл. 1. Что касается третьего этапа ( и ()), то неведущий ИР-элемент производит мультипликативных и аддитивных операций, а ведущий — соответственно ( операций приема и операций ожидания) и .

Таблица 2. К-во операций на втором этапе параллельной итерации информационного процесса обучения.

Метод	мульт. на ведущем	адд. на ведущем	мульт. на неведущем	адд. неведущем
Наискор. спуска
QuickProp
RPROP

Поскольку первый этап требует операций на ведущем ИР-элементе и на, второй — и , а третий на неведущем то перед началом приема ведущий ИР-элемент должен ожидать операций.

Таким образом, параллельный информационный процесс обучения совершает операций, а эффективность параллельных информационных процессов, использующих градиентные алгоритмы, можно расписать как для метода наискорейшего спуска и для RPROP

	(5)

(информационный процесс выполняет раз по операций параллельного алгоритма — операций выполняется последним шагом — и прочих операций)

		(6)
	(7)
	(81)

где — количество итераций, количество прочих операций алгоритма.

Список литературы

1. Крючин О.В. Разработка параллельных градиентных алгоритмов обучения искусственной нейронной сети // Электронный журнал "Исследовано в России", 096, стр. 1208-1221, 2009 г. // Режим доступа: http://zhurnal.ape.relarn.ru/articles/2009/096.pdf Загл. с экрана.

2. Крючин, О.В. Разработка параллельных эвристических алгоритмов подбора весовых коэффициентов искусственной нейронной сети / О.В. Крючин // Информатика и ее применение. — 2010. — Т. 4, Вып. 2. — C. 53-56.

3. Крючин, О.В. Параллельные алгоритмы обучения искусственных нейронных сетей / О.В. Крючин // Информационные технологии и математическое моделирование (ИТММ-2009) : матер. VIII Всерос. науч.-практ. конф. с междунар. участием, 12-13 ноября 2009 года. — Томск:, 2009. — Ч. 2. — С. 241-244.