А.И. Долгарев

ПЕРЕСЕЧЕНИЯ ЦИЛИНДРИЧЕСКИХ ПОВЕРХНОСТЕЙ

В 4-МЕРНОМ ЕВКЛИДОВОМ ПРОСТРАНСТВЕ

Аннотация. Исследуются поверхности 4-мерного евклидова пространства. Выделены 3-мерные цилиндрические поверхности, и цилиндрические поверхности, являющиеся 1-параметрическими и 2-параметрическими; 2-мерные цилиндрические 1-парамет-рические поверхности. Для всех поверхностей выписаны их касательные и нормальные плоскости. Найдены зависимости между коэффициентами форм кривизны и метрических форм некоторых поверхностей.

Ключевые слова: 3-мерные цилиндрические поверхности; пересечение цилиндрических поверхностей; нормали пересечений цилиндрических поверхностей; метрические формы и формы кривизны цилиндрических поверхностей и их пересечений.

Евклидово пространство размерности 4 содержит регулярные поверхности следующих видов. (I) 3-мерные 3-параметрические поверхности, заданные одной явной функцией ; (II) 3-мерные 2-параметрические цилиндрические поверхности, заданные одной явной функцией ; (III) 2-мерные 2-параметрические поверхности, заданные двумя явными функциями , ; (IV) 3- и 2-мерные 1-параметрические поверхности, заданные соответственно одной и двумя явными функциями , . Коэффициенты формы кривизны гиперповерхностей (I) и (II) являются функциями коэффициентов метрической формы поверхности. Всякая 2-мерная 2-параметрическая поверхность (III) является 2-мерным пересечением двух 3-мерных цилиндрических поверхностей (II), нормали 3-мерных цилиндрических поверхностей (II) есть нормали 2-мерной 2-параметрической поверхности (III), коэффициенты форм кривизны 2-мерной 2-параметрической поверхности (III) выражены через коэффициенты метрических форм пересекаемых цилиндрических поверхностей (II). Поверхности (IV) есть прямая сумма кривой и поверхности. Для всех поверхностей указаны касательные плоскости и нормали, соответственно нормальные плоскости.

2-параметрические поверхности 4-мерного евклидова пространства являются пересечением цилиндрических поверхностей. Гиперповерхности мерного евклидова пространства описываются погружениями мерного действительного многообразия в евклидово пространство , . Это явное задание поверхности, или поверхность-график. Функция , , меньшего числа параметров описывает ()-мерные цилиндрические поверхности в , [1]. Поверхность является гиперповерхностью в мерном подпространстве пространства и служит направляющей поверхностью цилиндрической поверхности пространства ; образующие цилиндрической поверхности составляют плоскость размерности пространства . Как погружение , поверхность обладает единственной нормалью. Символ в обозначении указывает на число параметров, описывающих поверхность , а не на размерность поверхности. На основе [1, лемма 4], выполняется:

1. ТЕОРЕМА. Всякое погружение определяет в пространстве параметрическую поверхность размерности . Поверхность размерности является либо гиперповерхностью, либо цилиндрической поверхностью. #

В [2, c. 184 – 186], внутри раздела 15, намечен подход к заданию мерных поверхностей в мерном евклидовом пространстве , . Поверхность размерности пространства , понимается как непустое пересечение гиперповерхностей пространства . Здесь требуется уточнение: указанное пересечение поверхностей должно быть мерным, но возможны пересечения размерностей от 0 до .

1. Поверхности евклидова пространства

1.1. Задание поверхностей

Пусть задано отображение , , где односвязная область, . В выбран некоторый ортонормированный репер , формулы замены реперов считаем дифференцируемыми, поэтому все рассмотрения можно проводить в выбранном репере без потери общности. Если , и , то , ; векторная функция

= , ,

определяет в поверхность от параметров. В области частные производные

векторной функции независимы; число независимых функций равно . Поверхность, удовлетворяющая приведенным условиям, как известно, является регулярной; точки, в которых поверхность регулярна, называются обыкновенными. Из математического анализа известно следующее утверждение.

А. ТЕОРЕМА. В окрестности каждой обыкновенной точки области функция может быть задана в параметризации (с точностью до нумерации параметров):

. #

Определено функций . Если , то поверхность может быть линией

,

При имеется параметрическая поверхность . При еcть гиперповерхность пространства . Размерность поверхности совпадает с размерностью ее касательной плоскости. Далее, задавая поверхность , используем обозначение

, (1)

Функция (1) задает поверхность от одной до трех явными скалярными функциями .

1.2. Поверхности пространства , заданные одной явной функцией.

Погружения могут быть 1,2,3-параметрическими.

(а) 3-параметрические поверхности . Погружение описываются одной явной функцией или векторной функцией вида (1):

= .

В окрестности всякой обыкновенной точки поверхности имеется 3 независимых вектора касательных: , , ; касательная плоскость 3-мерна,

=

и поверхность 3-мерна. Вектором нормали, согласно [1], является

, , (2)

нормаль поверхности есть = . Здесь скалярные произведения . Так как , то единичный вектор нормали таков

.

(б) 2-параметрические, т.е. 2-порожденные поверхности описываются явной функцией и векторной функцией:

= .

На поверхности лежат прямые линии , проходящие через точку в направлении вектора (подробнее в [1]). Касательные векторы: , и ; касательная плоскость

=

имеет размерность 3 и поверхность 3-мерна. Вектор нормали, согласно [1], есть , единственная нормаль поверхности такова: = .

(в) 1-параметрические, 1-порожденные поверхности описываются явной функцией: и векторной функцией вида (1)

= .

Касательные векторы , ; касательная плоскость = размерности 3 и поверхность имеет размерность 3. Вектор нормали есть , см. [1], и единственная нормаль 1-параметрической поверхности есть = .

(г) Имеется цилиндрическая поверхность = , (параметр от параметра не зависит) или поверхность = ; поверхности рассмотрены ниже в п. 3.

Касательные плоскости указанных выше поверхностей 3-мерны, и эти поверхности 3-мерны. Имеет место

2. ТЕОРЕМА. [1, п. 4] Поверхность , , пространства , заданная одной явной функцией, обладает единственной нормалью во всякой своей обыкновенной точке

= . #

В [1] указаны метрическая форма и форма кривизны поверхностей, заданных одной явной скалярной функцией и найдены, [1, теорема 13], , выражения коэффициентов формы кривизны через коэффициенты метрической формы поверхности. Значит, явно заданная поверхность определяется однозначно, с точностью до положения в пространстве, своей метрической формой. Тем самым, повышается значение метрической формы поверхности. В теории поверхностей важно не только знать, сколько касательных и нормальных векторов имеет поверхность, но и предъявлять эти векторы, т.е. записывать их в тех координатах, в которых задана поверхность.

2. 2-парамерические поверхности размерности 2

2.1. Пересечения 3-мерных поверхностей

Как уже отмечено, согласно [2], 2-мерные поверхности в являются пересечением двух 3-мерных поверхностей. 3-мерная 3-параметрическая поверхность описывается одной явной функцией трех параметров и векторной функцией

= .

2-параметрические 3-мерные поверхности описываются одной явной функцией и векторной функцией:

= ,

компонента от параметров не зависит.

Идея Дж. Торпа уточняется следующим утверждением.

3. ТЕОРЕМА. Всякая регулярная 2-параметрическая 2-мерная поверхность евклидова 4–мерного пространства является пересечением двух 2-параметрических 3-мер-

ных цилиндрических поверхностей.

# Произвольная регулярная поверхность пространства описывается 2-пара-метрической функцией

= , .

Это 2-параметрическое многообразие в . Поверхность рассматривается локально, в окрестности некоторой точки. Ввиду регулярности, согласно теореме А, в окрестности обыкновенной точки поверхность описывается в следующей параметризации

= , , . (3)

Тем самым, поверхность задана двумя явными скалярными функциями двух параметров. Многообразие (3) содержит два следующих 2-параметрических подмногообразия

: = , : = . (4)

Каждое из них является 3-мерной цилиндрической поверхностью в пространстве . Цилиндрическая поверхность имеет образующие, параллельные координатной оси . Образующие цилиндрической поверхности параллельны оси . Общие точки поверхностей и составляют поверхность . Уточним идею Дж. Торпа, [2, c. 184 – 186]. Мы получаем, что , по теореме А, есть пересечение 3-мерных цилиндрических поверхностей

: = ,

это 2-параметрическое многообразие, описываемое системой функций

: #

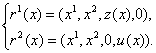2.2. Метрические формы 2-порожденных поверхностей

4. ТЕОРЕМА. Касательные плоскости

= , = и =

поверхностей и и их пересечения : = имеют размерности 3, 3 и 2 соответственно.

# Касательные векторы поверхности , см. (4), таковы

, и ;

они независимы, имеется касательная плоскость = , ее размерность равна 3 и размерность поверхности тоже равна 3. Касательные векторы поверхности , см. (4):

, и ;

касательная плоскость есть = , размерность ее равна 3.

Для поверхности : = имеем касательные векторы, см. (3),

, ; (5)

они неколлинеарны, т.е. выполняется условие

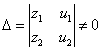; (6)

значит, касательная плоскость поверхности есть: = , ее размерность равна 2 и размерность поверхности тоже равна 2. #

5. ТЕОРЕМА. Коэффициенты метрических форм

, и (7)

поверхностей и и их пересечения : = вычисляются соответственно по формулам:

, , ; (8)

, , ; (9)

, , . (10)

Детерминанты метрических форм цилиндрических поверхностей и и поверхности равны соответственно

, , . (11)

Зависимости между коэффициентами метрических форм , соответственно цилиндрических поверхностей и и метрической формы их пересечения = таковы:

, , . (12)

# Полный дифференциал функции равен . Метрической формой поверхности является

.

Обозначим: . Имеем каноническую запись метрической формы поверхности в (7), коэффициенты метрической формы выписаны в (8). Метрической формой поверхности является

=.

После обозначения: метрическая форма поверхности имеет вид второй формулы в (7); ее коэффициенты см. в (9). Метрической формой поверхности является

.

Обозначив: , имеем каноническую запись метрической формы поверхности в (7), коэффициенты метрической формы есть (10).

Согласно значению детерминанта метрической формы поверхности, имеем: и т.д. . Соотношения (11) между коэффициентами получаются по (8), (9) и (10). #

2.3. Нормальная плоскость пересечения цилиндрических поверхностей

6. ТЕОРЕМА. Векторами нормалей каждой из 3-мерной цилиндрических поверхностей и являются соответственно векторы

, , (13)

и единственные нормали поверхностей таковы:

= , = .

Нормальная плоскость пересечения = цилиндрических поверхностей есть

=,

она 2-мерна и порождается нормалями цилиндрических поверхностей и .

# Векторы нормалей каждой из поверхностей , , согласно [1], вычисляются как бивекторы , , и 3-мерные поверхности в обладают единственной нормалью. Проверка показывает, что для скалярных произведений векторов выполняются равенства:

, , , .

Значит, векторы нормальны касательной плоскости = . #

Модули векторов нормалей (13):

, . (14)

Нормальные векторы соответственно поверхностей ,, являющиеся нормальными и для поверхности , назовем основными нормальными векторами поверхности , являющейся пересечением цилиндрических поверхностей ,.

7. ТЕОРЕМА. На основе касательных векторов (5) поверхности получаются следующие независимые векторы нормалей поверхности

, . (15)

Первый из них есть сумма векторов нормалей пересекающихся цилиндрических поверхностей = :

= + .

# Один вектор нормали поверхности запишем по виду векторов нормали (13) на основе векторов касательных (5): ; имеем скалярные произведения векторов , , т.е. , . Другой вектор нормали находим из условий , , это второй вектор из (15). Векторы и неколлинеарны, поэтому нормальная плоскость поверхности в точке такова =, она 2-мерна. #

Модули векторов нормали (15):

, . (16)

По теореме 6, =. Нормальная плоскость поверхности содержит бесконечное множество нормалей поверхности. В нашем случае выполняется

8. ТЕОРЕМА. Нормальная плоскость пересечения = есть

==. #

2.4. Формы кривизны цилиндрических поверхностей и

и их пересечения

В координатах на поверхностях и и = рассматривается кривая в естественной параметризации

,

где естественный параметр кривой. Имеем вектор касательной к кривой :

и соответствующие векторы касательных к линиям , на поверхностях , ; где имеются небольшие отличия в символах. Так как вектор касательной к линии в естественной параметризации является единичным, то получаем единичный вектор главной нормали линии на поверхности :

(17)

и векторы , соответственно на поверхностях , .

9. ТЕОРЕМА. Нормальная кривизна линий на поверхности = относительно нормалей соответственно равна

= , (18)

= , (19)

= . (20)

# Перемножим скалярно векторы , и вектор (17) на единичные векторы нормалей (13) и (15) к поверхностям. При этом произведение второго слагаемого в (17) и вторых слагаемых в , на векторы (13) и (15) равны нулю. Имеем векторы вторых производных:

, , . (21)

, , . (22)

, , . (23)

Нормальная кривизна линии на поверхности относительно первой нормали из (13) равна

= = , (24)

а нормальная кривизна линии на поверхности относительно второй нормали из (11) равна

= = . (25)

Нормальная кривизна линии на поверхности = относительно нормали в (15) такова

= =

= . (26)

Итак, получены все равенства из формулировки доказываемого утверждения. #

Нормальные кривизны и линий на поверхности относительно основных нормальных направлений поверхности , считаем основными. Нормальная кри-визна линий на поверхности не относится к основным. Выражения для коэффициентов формулы по виду как-то связаны с коэффициентами формул и , но функ-циональной зависимости нет.

Запишем еще нормальную кривизну линии на поверхности = относительно другой нормали из (15) :

= =

= +

+. (27)

Модули векторов нормали есть (16). Однако, нормальную кривизну относительно всех нормалей поверхности выписать невозможно. Ограничимся нормальными кривизнами , , , (18) – (20).

10.ТЕОРЕМА. Формы кривизны поверхностей , и = таковы

= , = , ; (28)

их коэффициенты равны

, , . (29)

# По формулам (18) – (20) запишем равенства:

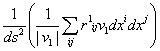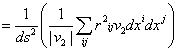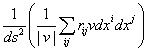= ,,= . (30)

В слагаемых полученных сумм введем обозначения (29). Выражения в скобках являются квадратичными формами (28). #

11. ТЕОРЕМА. Нормальные кривизны линий на поверхностях , и соответственно с формами кривизны и метрическими формами связаны соотношениями

= , = , = .

# Согласно формулам (28) – (30), указанные равенства выполняются. #

Нормали (13) поверхности являются и нормалями соответственно поверхностей , , теорема 6. Поэтому выполняется

12. ТЕОРЕМА. Основные формы кривизны поверхности совпадают соответственно с формами кривизны поверхностей и , т.е. первая в (28) форма кривизны поверхности является и формой кривизны поверхности , а вторая в (28) форма кривизны поверхности является формой кривизны поверхности .

# Четвертая компонента вектора нулевая, см. (13); третьи компоненты векторов (21) и (23) одинаковы, поэтому для скалярных произведений векторов имеем

.

Третья компонента вектора равна 0, см. (13), значит, по (22) и (23):

.

На этом основано совпадение соответствующих квадратичных форм. #

13. ТЕОРЕМА. В компонентах векторов производных коэффициенты формы кривизны 2-мерной 2-параметрической поверхности = , являющейся пересечением двух цилиндрических 2-параметрических 3-мерных поверхностей , , и коэффициенты форм кривизн поверхностей , , детализируются следующим образом

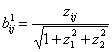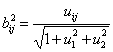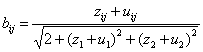, , ; (31)

однако + .

# Указанные коэффициенты отыскиваются по формулам (18) – (20) и формулам (29), (13), (15). Неравенство очевидно. #

Как показывают формулы (31), нет зависимостей между коэффициентами форм кривизны поверхностей , и коэффициентами формы кривизны поверхности , хотя для коэффициентов метрических форм поверхностей , и зависимости имеются, см. (12).

Коэффициенты формулы (27) нормальной кривизны линий на поверхности относительно нормали , второй в (12), и связанной с ней формы кривизны поверхности сложнее коэффициентов (27), что закономерно. Обычно используются основные формы кривизны, к которым относятся первые две в (28).

2.5. Выражение коэффициентов формы кривизны поверхности =

через коэффициенты метрической формы поверхности

В [1] найдены выражения коэффициентов формы кривизны поверхности евклидова пространства , , в случае, если поверхность задана одной явной функцией:

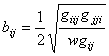, , . (32)

В случае поверхностей 3-мерного евклидова пространства аналогичные формулы получены в [3] в другой символике. Коэффициенты формы кривизны имеют вид (32) при замене на, см. (11), ; коэффициенты формы кривизны имеют вид (32) при замене на, см. (11) . В связи с этими фактами, выполняется

14. ТЕОРЕМА. Коэффициенты основных форм кривизны и поверхности выражаются соответственно через коэффициенты метрических форм и поверхностей , по формулам (в соответствии с [1])

, , ;

, , . #

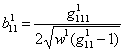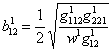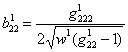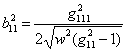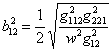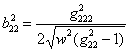Коэффициенты форм (8) и (10), а также (9) и (10) не совпадают, поэтому метрические формы поверхностей , не совпадают с метрической формой поверхности .

Для неосновных форм кривизны поверхности зависимости вида (32) не выполняются; это верно и для формы кривизны относительно нормального вектора (26).

Таким образом, в основных нормальных направлениях поверхности имеются зависимости коэффициентов форм кривизны поверхности от коэффициентов метрических форм цилиндрических поверхностей , , в пересечении дающих поверхность . Но нет зависимости коэффициентов формы кривизны поверхности от метрической формы этой поверхности.

3. Поверхности, описываемые функцией с одним параметром

В случае (г) п. 1.2. указаны две 1-параметрические цилиндрические поверхности:

: = ; : = ;

(параметр от параметра не зависит). Имеются касательные плоскости

= ; = ;

где , .

15. ТЕОРЕМА. Существует два вида 1-парметрических цилиндрических поверхностей 4-мерного евклидова пространства. Одна из них 3-мерная с единственной нормалью в каждой точке; другая 2-мерная, обладающая 2-мерной нормальной плоскостью.

# Поверхность цилиндрическая с образующими, параллельными координатной оси и направляющей = в координатной 3-плоскости . Нормаль линии лежит в этой же 3-плоскости. Поверхность 2-мерная. Вектор нормален поверхности . Вектор другой нормали поверхности есть = , см. векторы в (13). Нормальная плоскость такова: = . Поверхностьцилиндрическая с образующими, параллельными координатной 2-плоскости и направляющей = в координатной 2-плоскости . Нормаль линии лежит в этой же 2-плоскости. Поверхность 3-мерная. Вектор нормален поверхности и определяет единственную нормаль поверхности = . #

Наряду с линиями, которые описываются 1-параметрическими функциями, в 4-мерном евклидовом пространстве содержатся 1-параметрические поверхности, одна из таких поверхностей имеет 2-мерную нормальную плоскость. 2- и 1-порожденные поверхности, заданные одной явной функцией, являются цилиндрическими. Не всякая 1-парамет-рическая поверхность является линией, возможно это цилиндрическая поверхность.

Заключение

Выполненные исследования выявили значение цилиндрических поверхностей во множестве всех поверхностей, зависимости между размерностью и числом параметров поверхности, связи между метрическими формами и формами кривизны поверхностей. Намечены методы получения нормалей к поверхностям. 1-параметрические поверхности оказались разнообразными.

Список литературы

1. Долгарев А.И. Многомерные поверхности I. Выражение коэффициентов второй квадратичной формы евклидовой поверхности через коэффициенты первой квадратичной формы.// Materialy X Miedzynarodowej naukowi-praktycznej konferencji “Moderni vymozenosti vedy – 2014”, dil 34. Matematyka. Fizyka. – Praga. Publiching House “Education and Skience”. s.r.o. – 2014. С. 30 – 40.
2. Торп Дж. Начальные главы дифференциальной геометрии. Волгоград: «Платон», 1998 – 360с
3. Долгарев А.И. Новый вид основной теоремы Гаусса в евклидовой теории поверхностей. //Materiali IX mezinarodni vedecko-praktika conference «Dni vedy – 2013» - Dil 32. Matematika. Vystavba a archtektura: Praga. Publiching House “Education and Skience”. s.r.o. – 2013. С. 55 – 60.