Комолов В.М.

 Украинская инженерно-педагогическая академия, г. Харьков

Обобщение Теорем сложения для Тригонометрических функций  

       

Введение. Теорема косинусов – одна из основных в математике: длина стороны с косоугольного треугольника, лежащая против угла γ, определяется через две другие стороны  а, b и угол γ:   

                                                                                         (1)

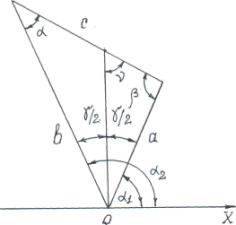  Пусть известны углы, которые определяют положение сторон а, b, по отношению к оси абсцисс, т.е. ориентация треугольника в прямоугольной системе координат (рис.1).

                                                 Рисунок 1.

Необходимо найти угол, определяющий ориентацию стороны с. Однако, прежде чем определить его в явном виде, изложим наводящие соображения. Произведем формальные преобразования под знаком радикала в (1):

a2+b2–2abcosγ=2ab∙[(a/b+b/a)/2 – cosγ ]= 2ab[(eln(a/b)+ e-ln(a/b))/2 – cosγ].

 Обозначим

                                                                  ln(a/b) = τ ,                                       (2)

 и, подставив в вышеприведенное соотношение, получим:

a2+b2–2a∙b∙cosγ=2a∙b∙[(eτ+e–τ)/2 – cosγ] = 2ab∙[chτ–cosγ].                                                                     

Выражение в квадратных скобках представляет собой квадрат модуля комплексной функции:

chτ–cosγ =2∙(1/2)∙[ch(2∙(τ/2))–cos(2∙(γ/2))=2∙|sh(τ±γ)/2|2=2|sh[ln±iγ/2]|2          (3)

Поскольку sh(iz) = i∙sin(z), то

                                   chτ – cosγ = 2∙|sin[(γ /2) ± i∙ln]|2   .                                                          (4)

     Используя форму  (3), получим, что

                         =                                                            (5)

 Будем считать, что в (5) c представляет собою модуль комплексного числа  ceiθ. Аргумент θ можно определить через аргумент функции sh[(τ ±iγ)/2] и углы α1,α2, которые определяют направление векторов   и    .

          Основная часть. Пусть заданы комплексные числа z1=a∙exp(iα1), z2=b∙exp(iα2), где углы α1 и α2 отсчитывают от оси абсцисс в положительном направлении (против часовой стрелки, см. рис.2). Определим модуль и аргумент суммы и разности комплексных чисел z1±z2.

 z1+z2=|z1+z2|∙eiθ=∙[ +]=2∙∙(1/2)[exp(ln)+

                        +exp(-ln)]=2∙ch[ln]=

                        =2∙∙ch[ln+i(α1–α2)/2].                                      (6)

Отсюда  модуль суммы и аргумент θ:

|z1+z2|=|+ |=2∙|ch[(τ/2)+i(α1–α2)/2]|=    (7)

        θ=arg(z1+z2)= (α1+α2)/2 +arctg{[(a–b)/(a+b)]∙tg((α1–α2)/2)}.                           (7')

В этом выражении второе слагаемое есть arg{ch[ln+i((α1–α2)/2]}. Поведение функций вида  y=arctg(s∙tgx)   при  0<s<∞ и – ∞<х<∞ рассмотрим ниже. Формулы, аналогичные (7),(7'), получим и для разности комплексных чисел z1–z2:

                z1–z2=|z1–z2|∙eiψ=2∙sh[ln]=±2∙∙exp(i(α1+α2)/2)

                                      sh[ln+i(α1–α2)/2]                                                   (8)  

 Выделим  в (8) модуль и аргумент

  |z1–z2|=|–|=2∙|sh[(τ/2)+i((α1–α2)/2]|=;   (9)

           ψ = arg (z1–z2)= (α1+α2)/2 + arctg[((a+b)/(a–b))∙tg((α1– α2)/2)].                      (9')

Таким образом, длину вектора   (рис. 2)  определяет

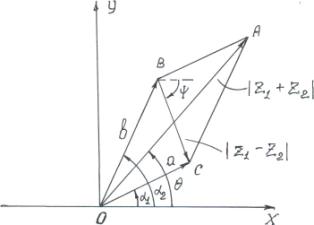
                                                    Рисунок 2.

 соотношение (7), а его положение по отношению к оси ОХ – характеризует угол θ – (7'). Аналогично, длину вектора определяет соотношение (9), а угол ψ – (9'). Выделяя в (6) и (8)  действительные и мнимые части, получим формулы для суммы и разности двух тригонометрических функций  общего вида, т.е. при произвольных амплитудах и аргументах:

                          a∙sinα1±b∙sinα2 =

                 sin{(α1+α2)/2+arctg[(()/(a±b))∙tg((α1– α2)/2)]};                            (10)

                           a∙cosα1±b∙cosα2 =

                 cos{(α1+α2)/2+arctg[(()/(a±b))∙tg((α1 – α2)/2)]}.                            (11)

 В этих  формулах  а и b действительные величины и  оба больше нуля: a>0,b >0.

 Из (10), (11) получим еще одну формулу сложения тригонометрических функций:

                                   a∙cosα1+bsinα2 =

                       cos{((α1+α2)/2) –π/4+arctg[((a–b)/(a+b))∙tg((α1–α2)/2+π/4)]}.         (12)

         В частном случае, когда α1=α2, формула (12) переходит в известное соотношение для сдвига аргумента [1,2], если учесть равенство:

                                arctgs + arctg[(1-s)/(1+s)]= π/4  .                                            (13)

          Установим геометрический смысл сомножителей, которые входят в формулы (6), (8) и (10), (11). Амплитуды суммы (разности) двух гармонических функций определяют соотношения (7), (9). Как было показано выше, это есть длина каждой из диагоналей параллелограмма (рис. 2), положение сторон которого определяют  векторы z1=a∙exp(iα1), z2=b∙exp(iα2), где (α1+α2)/2,- угол, характеризующий положение биссектрисы угла γ по отношению к оси ОХ  (рис.1). Второе слагаемое в (7') есть угол δ между биссектрисой и медианой, выходящих из вершины одного и того же угла треугольника.

             δ  = arctg[((a–b)/(a+b))∙tg(γ/2)],  δ< 0 ,  a <  b  ;     δ >0 ,a >  b  .               (14)

Поэтому θ = (α1+α2)/2 +δ .

Второе слагаемое в (9') с точностью до π есть  угол ν, который образует биссектриса угла γ с противолежащей стороной треугольника с. Определим угол ν, используя теорему тангенсов (формулу Региомонтана [1,2]). Для треугольника на рис.1:

                              (a–b)/(a+b) =tg((α–β)/2)/ctg((α2–α1)/2)] .                                   (15)

 Из рассмотрения треугольников, которые имеют в качестве общей стороны биссектрису  ОМ (рис. 1), следует что ν = π/2 + (α–β)/2. Из (15)

                           (α–β)/2= arctg[((a–b)/(a+b))∙ctg((α2–α1)/2)]                                   (16)

Таким образом,     

                        ν =  π+ arctg[((a+b)/(a–b))∙tg((α1–α2)/2)];                                         (17)

                       ψ = ±{(α1+α2)/2 + arctg[((a+b)/(a–b))∙tg((α1–α2)/2)]}.

Соотношение для угла ψ с точностью до знака совпадает с (9'). При преоб-разовании (16) в (17) использовано соотношение  arctgx+arctg(1/x)=π/2.

          Приложение. В качестве примера рассмотрим суперпозицию двух гармонических колебаний одинаковой частоты ω, но различных амплитуд А, В и начальных фаз φ1,φ2: Аsin(ωt+φ1) и Bsin(ωt+φ2). Из формулы (10) следует: 

                     Аsin(ωt+φ1) + Bsin(ωt+φ2)=

                 sin{ωt + (φ1+φ2)/2+}.     

 В этом выражении первый сомножитель (радикал) есть амплитуда результирующего колебания, а аргумент синуса – его  фаза.  Два слагаемых в аргументе синуса, стоящие после ωt, представляют собой начальную фазу  результирующего колебания. Она существенно зависит как от амплитуд А, В, так и начальных фаз φ1,φ2 исходных сигналов. При равенстве амплитуд последних начальная фаза результирующего сигнала равна (φ1+φ2)/2. Максимум амплитуды последнего возникает при  равенстве начальных фаз исходных, т.е. при  φ1–φ2 =0 и равна сумме их амплитуд: |A+B|. Минимум амплитуды этого колебания наступает при φ1–φ2 =π (исходные колебания находятся в противофазе) и равен |A–B|.

Выводы: Таким образом, в работе получены формулы сложения для синусоидальных  (косинусоидальных) функций общего вида,  которые обобщают их на случай произвольного соотношения между амплитудами и аргументами.

          В заключение выражаю благодарность доц. Латынину Ю.М. за ценные замечания и помощь в работе.

             Литература:

1.     Бронштейн И.Н., Семендяев К.А. Справочник по математике  для инженеров и втузов. -13-е изд..- М.: Наука, гл. ред. физ.-мат. лит. 1986.- 544 с.

2.     Корн Г., Корн Т. Справочник по математике для научных работников и инженеров.- М.: Наука, 1984.-831с.