А.И. Долгарев

ФОРМЫ КРИВИЗНЫ ПЕРЕСЕЧЕНИЯ ЦИЛИНДРИЧЕСКИХ ПОВЕРХНОСТЕЙ

АННОТАЦИЯ. Поверхности размерности евклидова пространства размерности , , могут быть получены как пересечения многомерных цилиндрических поверхностей. Нормальные векторы цилиндрических поверхностей нормальны и поверхности их пересечения. Выписаны метрические формы и формы кривизны цилиндрических поверхностей и их пересечения. Установлена зависимость коэффициентов формы кривизны поверхности от коэффициентов метрических форм цилиндрических поверхностей.

Ключевые слова: многомерная цилиндрическая поверхность; нормали пересечения поверхностей; метрические формы и формы кривизны поверхности; коэффициенты форм кривизны как функции коэффициентов метрических форм поверхности.

Изучение поверхностей 4-мерного евклидова пространства в [1] выявляет некоторые закономерности и свойства поверхностей мерного пространства . Основополагающее значение имеют погружения мерного многообразия , в . Погружение и поверхность записывается в виде:

. (1)

Это поверхность-график, или явно заданная поверхность. В выбран некоторый ортонормированный репер , формулы замены реперов считаем дифференцируемыми, поэтому все рассмотрения без потери общности можно проводить в выбранном репере. В [2] в случае поверхность задается векторной функцией

.

Если , то, разумеется, поверхность описывается векторной функцией

, (2)

компоненты , не зависят от параметров ; . В случае поверхность является цилиндрической и содержит плоскость, состоящую из прямолинейных образующих , проходящих через точку поверхности в направлении вектора (подробнее об этом в [3]). Поверхность является мерной только в , где она гиперповерхность, при поверхность является параметрической; цилиндрические поверхности в имеют размерность , [3]. Значение цилиндрических поверхностей возрастает после [1] и усиливается ниже. В [4, c. 184 – 186], внутри раздела 15, мерные поверхности в мерном евклидовом пространстве , , понимаются как непустое пересечение гиперповерхностей пространства (но возможно пересечение, имеющее размерность от 0 до ).

В общем случае регулярная поверхность параметров пространствазадается в отображении . Если , и , то

= , ,

где , . Из математического анализа известно следующее утверждение.

А. ТЕОРЕМА. В окрестности каждой обыкновенной точки области функция может быть задана в параметризации (с точностью до нумерации параметров):

=. # (3)

Определено = скалярных функций , , При , поверхность может быть линией

,

При имеется параметрическая поверхность . Верхний индекс указывает на число параметров в задании поверхности. При , еcть гиперповерхность пространства . Размерность поверхности совпадает размерностью ее касательной плоскости. Функция (3) задает поверхность от одной до явными скалярными функциями вида (1). Если все функции в (3) кроме одной, от не зависят, то поверхность (3) цилиндрическая вида (2), задается одной явной функцией .

1. Касательная и нормальная плоскости поверхности размерности

Рассматривается случай , .

1.2. Поверхность как пересечение цилиндрических поверхностей

Пусть поверхность задана явными скалярными функциями или одной векторной функцией (3). Уточним идею Дж. Торпа задания поверхности как пересечения поверхностей.

1. ТЕОРЕМА. Всякая регулярная параметрическая мерная поверхность (3) евклидова –мерного пространства является пересечением параметрических мерных цилиндрических поверхностей.

# Согласно теореме А, всякая регулярная поверхность пространства в окрестности своей обыкновенной точки задается в параметризации (3). Это есть задание поверхности явными скалярными функциями вида (1), каждая такая функция описывает в цилиндрическую поверхность вида (2):

: =, . (4)

Координаты всякой точки поверхности удовлетворяют функции (3), т.е. каждой функции (4) и обратно. Таким образом, поверхность является пересечением цилиндрических поверхностей (4):

. (5)

Размерность каждой из поверхностей равна . #

1.2. Касательные плоскости мерной поверхности

В области частные производные

векторной функции независимы; число независимых функций равно . В репере производные функции таковы

, (6)

ненулевые компоненты имеют номера . Вместе с точкой поверхности векторы порождают касательную плоскость

= . (7)

Поверхность мерна, .

Каждая из цилиндрических поверхностей (4) имеет векторы касательных

, , (8)

сюда вошли векторы репера пространства, порождающие прямолинейные образующие цилиндрической поверхности. Касательная плоскость цилиндрической поверхности есть

= ;

Ее размерность равна . Значит, каждая поверхность обладает единственной нормалью.

1.3. Нормальная плоскость мерной поверхности

Вектор нормали плоскости таков:

= , , (9)

здесь является номером компоненты, равной 1. Этот вид нормали поверхностей, заданных одной явной функцией получен в [3]. Действительно, скалярные произведения векторов из (8) и вектора (9) равны нулю: векторы базиса указаны в (8). Имеем нормаль поверхности :

= ,

Она единственна в каждой точке.

2. ТЕОРЕМА. Нормальная плоскость пересечения (5) цилиндрических поверхностей порождается нормалями этих цилиндрических поверхностей:

= ,

ее размерность равна .

# Для векторов и касательных векторов , ; см. (9) и (6); имеем скалярные произведения: , т.е. и ; при этом . #

Понятно, что поверхность имеет и другие нормальные векторы. Векторы нормалей называем основными для поверхности . Модули основных векторов нормалей равны

. (10)

2.Метрические формы и формы кривизны поверхностей

2.1.Метрические формы поверхностей

По полным дифференциалам рассматриваемых функций (3) и (4)

, , , (11)

напишем метрические функции поверхностей и .

3. ТЕОРЕМА. Коэффициенты метрических форм

, , и (12)

поверхностей и их пересечения : вычисляются соответственно по формулам:

, , ; (13)

, , . (14)

Зависимости между коэффициентами метрических форм , цилиндрических поверхностей и метрической формы их пересечения таковы:

, . (15)

# По полному дифференциалу функций , см. (11), получаем метрические формы поверхностей

.

Обозначим: . Имеем каноническую запись метрических форм поверхностей в (12), их коэффициенты выписаны в (13). Метрической формой поверхности является

.

Обозначив: , имеем каноническую запись метрической формы поверхности в (12), коэффициенты метрической формы есть (14).

Соотношения (15) между коэффициентами получаются по (13) и (14). #

2.2. Формы кривизны цилиндрических поверхностей и их пересечения

В координатах на поверхностях и рассматривается кривая

,

где естественный параметр кривой. Имеем вектор касательной к кривой :

и соответствующие векторы касательных к линиям на поверхностях (имеются небольшие отличия в символах). Так как вектор касательной к линии в естественной параметризации является единичным, то получаем единичный вектор главной нормали линии на поверхности :

(16)

И аналогично векторы соответственно на поверхностях .

4. ТЕОРЕМА. Нормальные кривизны линий на поверхности относительно основных нормалей равны

= , где (17)

# Перемножим скалярно векторы , см. (16), на единичные векторы нормалей , см. (9), к поверхности. При этом произведение второго слагаемого в (16) на векторы равны нулю. Согласно (6), векторы вторых производных:

. (18)

Нормальная кривизна линии на поверхности относительно каждого вектора основной нормали (9) = равна

= , . (19)

По (18) и (9):

. (20)

Имеется нормальных кривизн линии на поверхности относительно ее нормалей (9). #

Нормальные кривизны линий на поверхности относительно основных нормальных направлений поверхности , считаем основными. Можно указать для поверхности неосновную нормаль , являющуюся суммой основных нормалей, кривизна линий на поверхности относительно нормали дает пример неосновной кривизны . Нормальную кривизну линий на поверхности относительно всех нормалей поверхности выписать невозможно.

5.ТЕОРЕМА. Формы кривизны поверхности таковы

= ; (21)

их коэффициенты равны

. (22)

В компонентах векторов производных коэффициенты формы кривизны мерной параметрической поверхности , являющейся пересечением цилиндрических параметрических мерных поверхностей , детализируются следующим образом

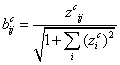. (23)

# Формулы (19) перепишем в виде:

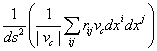= . (24)

В слагаемых рассматриваемой суммы (24) введем обозначения (22). Выражения в скобках являются коэффициентами квадратичных форм (21). Зная скалярные произведения , см. (20), по (9), (18), приходим к (23). #

Нормали (9) поверхности являются и нормалями соответственно поверхностей , см. теорему 2, поэтому выполняется

6. ТЕОРЕМА. Основные формы кривизны поверхности совпадают соответственно с формами кривизны цилиндрических поверхностей .

# Справедливы равенства (20), которые означают выполнимость утверждения. #

7. ТЕОРЕМА. Нормальные кривизны линий на поверхностях и соответственно с формами кривизны? и метрическими формами связаны соотношениями

= , = .

# Согласно формулам (12), (21) и (24), указанные равенства выполняются. #

По аналогии с (23) вычисляем коэффициенты относительно неосновной нормали :

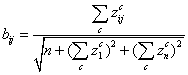; (25)

очевидно,

.

Однако, как показывают формулы (23) и (25), нет зависимостей между коэффициентами форм кривизны поверхностей и коэффициентами формы кривизны поверхности , хотя для коэффициентов метрических форм поверхностей и зависимости имеются, см. (15). Далее используются основные формы кривизны.

3. Выражение коэффициентов формы кривизны поверхности

через коэффициенты метрических форм поверхностей

В [3] найдены выражения коэффициентов формы кривизны поверхности евклидова пространства , , в случае, если поверхность задана одной явной функцией:

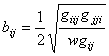, , . (26)

В случае поверхностей 3-мерного евклидова пространства аналогичные формулы получены в [6] в другой символике. Коэффициенты формы кривизны имеют вид (26) при замене на, см. (10). В связи с этим фактом, выполняется

8. ТЕОРЕМА. Коэффициенты основных форм кривизны поверхности выражаются через коэффициенты метрических форм поверхностей по формулам

, . #

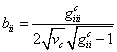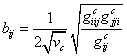Коэффициенты форм (13) и (14) не совпадают, поэтому метрические формы поверхностей не совпадают с метрической формой поверхности .

Таким образом, в основных нормальных направлениях поверхности имеются зависимости коэффициентов форм кривизны поверхности от коэффициентов метрических форм цилиндрических поверхностей , в пересечении дающих поверхность . Но нет зависимости коэффициентов формы кривизны поверхности от коэффициентов метрической формы этой поверхности.

Заключение

Выполненные исследования подтвердили значение многомерных цилиндрических поверхностей во множестве всех поверхностей, а также зависимости между размерностью и числом параметров поверхности, связи между метрическими формами и формами кривизны цилиндрических поверхностей. Нормали цилиндрических поверхностей являются нормалей их пересечения.

Список литературы

1. Долгарев А.И. 2-поверхности 4-мерного евклидова пространства. // Materialy X Miedzynarodowej naukowi-praktyeznej konferencji “Aktualne problem nowoczesnych nauk – 2014”, Volume 23. Matematika. Chemia i chemiczne technologie. – Premysl. Nauka i studia, 2014. P. 33 – 41.

2. Иванов А.О., Тужилин А.А. Лекции по классической дифференциальной геометрии. – М.: Новая университетская библиотека, 2009 – 233с.

3. Долгарев А.И. Многомерные поверхности I. Выражение коэффициентов второй квадратичной формы евклидовой поверхности через коэффициенты первой квадратичной формы.// Materialy X Miedzynarodowej naukowi-praktycznej konferencji “Moderni vymozenosti vedy – 2014”, dil 34. Matematyka. Fizyka. – Praga. Publiching House “Education and Skience”. s.r.o. – 2014. С. 30 – 40.

4. Торп Дж. Начальные главы дифференциальной геометрии. Волгоград: «Платон», 1998 – 360с.

5. Иванова-Каратопраклиева И., Марков П.Е., Сабитов И.Х. Изгибание поверхностей. III. – Фундаментальная и прикладная математика, том 12. (2006), № 1, С. 3 – 56.

6. Долгарев А.И. Новый вид основной теоремы Гаусса в евклидовой теории поверхностей. //Materiali IX mezinarodni vedecko-praktika conference «Dni vedy – 2013» - Dil 32. Matematika. Vystavba a archtektura: Praga. Publiching House “Education and Skience”. s.r.o. – 2013. С. 55 – 60.