Kraeva E.M., Masich I.S.

Siberian State Aerospace University

named after academician M. F. Reshetnev, Russia

The criterion function and its modification in construction of patterns for a classification model

A modification of the criterion function of the optimization model in the method of logical analysis of data to increase different rules in the classification model is proposed. The empirical confirmation of the advisability of modifying the criterion function is given.

In [1] we have considered the optimization model, the decision of which is patterns in the data to construct the classifier.

Denote Ω_s⁺ and Ω_s⁻ are sets of n-dimensional binary vectors of positive and negative classes constituting the training data set.

The basis of this approach is the notion of a pattern. A positive pattern called a subcube of the space of Boolean variables B₂^t, which intersects the set Ω_s⁺ and has a limited number of elements in common with the set Ω_s⁻. Negative pattern is defined similarly.

A positive ω-pattern for ω{0,1}^t is a pattern containing a point ω.

We define corresponding subcube using variables y_j:

Optimization model has the following form.

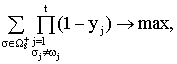(1)

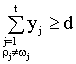for every , . (2)

According to the criterion (1), we seek to maximize the coverage of the resulting pattern, i.e. the number of objects captured with the pattern. Each subsequent pattern maximizes its coverage, capturing objects that are representative of the class, and atypical class objects remain uncovered and in the final rule there are no patterns that take into account the objects of the class. Therefore, we obtain a set of similar patterns for the class, thereby reducing the quality of the classification. To obtain a classification model with higher different patterns, which can allocate significantly different subsets of objects, we propose to modify the criterion (1) as follows:

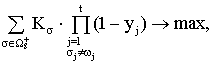(3)

where K_σ – is weight of the positive observations σΩ_s⁺, which is reduced when this observation is covered, thereby reducing its priority to participate in the formation of the next pattern in favor of uncovered observations.

In order to use the criterion (3) for the formation of patterns, it is necessary to set the initial weight for all objects and rule changes weights for objects that participated in the formation of the current pattern. We offer the initial weights is set to 1 for each object in the training set. Rule of changes for the weight of the object, which took part in the formation of this pattern:

,

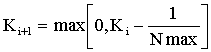where K_i, K_i+1 are weights of the covered object to the formation the current pattern and the next pattern, Nmax is parameter defined by the researcher, which means the maximum number of patterns that can cover the training sample object in the model.

Parameter Nmax for each class is given in the range from 1 to the maximum number of patterns constructed for this class. If Nmax is set to close or equal to the maximum number of patterns for this class, then the value of the criterion (3) tends to the value the criterion (1) for each pattern in the model, therefore, the new model works similarly to the previous classification. If Nmax tends to 1, then the number of patterns with a value of the criterion (3) greater than 0 is reduced, because initially all objects are captured and their weights are reset. In the new classification model, insufficient number of patterns is presented, which eventually is not capable to classify new incoming objects, i.e. classification quality decreases.

Thus, using the criterion (3), we obtain the patterns that cover substantially different subset of the objects.

According to the results obtained it can be noted that the use of an optimization model with the criterion (3) allows to simplify the classification model, reducing the number of patterns in the model in 2-3 times compared to the full set for a specific task. The accuracy of classification is not decreased or is decreased only slightly. When the optimization model with the criterion (3) is used, average degree of patterns becomes smaller, which means that the patterns themselves become clearer and easier to interpret.

The work is supported by the Grant of President of Russian Federation MK-1371.2013.8.

References

1. Masich I.S. Pattern search in data for solving practical problems of recognition. Materiály VIІI mezinárodní vědecko - praktická konference «Zprávy vědecké ideje - 2012». – Díl 21. Matematika. Fyzika: Praha. Publishing House «Education and Science», p. 14-15.