Каладзе В.А.
ОПИСАНИЕ ДИНАМИКИ СЛУЧАЙНЫХ ПРОЦЕССОВ
В работе предложено решение проблемы
статистической идентификации сложных эволюционирующих систем, информационно
представленных динамическими случайными процессами.
Детерминированный динамический хаос в нелинейных
динамических системах наблюдается, если исследователь использует формальную
математическую модель в виде задачи Коши [1]. Другими словами, хаос «вызван к
существованию» самим исследователем и связан не с некоторой особенностью
реальной сложной динамической системы, а с неадекватным её представлением. Хаос
в динамике указывает не только на неадекватность системы дифференциальных
уравнений, возникающую в процессе эксплуатации математической модели, но и на чувствительность
динамической эволюции к изменениям начальных условий задачи.
В этом случае альтернированность системы
(определение Я.З. Цыпкина и Я.Н. Ройтенберга) указывает на внезапное нарушение
согласованности реальной сложной системы и её динамической модели, что приводит
к существенному расхождению фазовых траекторий системы и модели [2].
В большинстве задач исследования сложных
систем отсутствуют данные о возмущающих факторах и единственной исходной информацией
об объекте является его отклик, как реализация нестационарного случайного процесса,
а в дискретном времени – случайная временная последовательность (time series).
В последнем случае обосновано применение алгоритмических моделей, представляющих собой рекуррентную вычислительную
процедуру.
Это позволяет описывать и прогнозировать
динамику объекта без привязки к его внутренней структуре только по реализации нестационарного
случайного процесса на его выходе, который у эволюционирующей системы следует
рассматривать как динамический [3].
Важным классом динамических случайных
процессов, отражающим эволюционные изменения в сложной системе, по
классификации А.Н. Колмогорова [4] являются процессы со стационарными
приращениями. Если низкочастотная компонента случайной функции Y(t) не оказывает
влияния на значение разности
F(t) = Õ[Y(t)] = Y(t) – Y(t – τ) при τ = const,
то случайная функция времени F(t) оказывается
стационарной. В этом случае функцию Y(t) называют случайной функцией со
стационарными первыми приращениями.
Если стационарно приращение n-го порядка
[5]
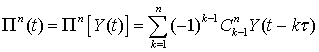 ,
,
то Y(t) – случайный процесс со стационарными
приращениями n-го порядка.
Такая классификация позволила, на основе
группового закона эволюции [6], сформировать в дискретном времени алгоритмические
динамические предикторные модели (ДПМ) [7], например, третьего порядка
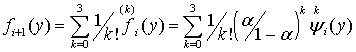 ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
где ![]() – вектор каскадной
фильтрации,
– вектор каскадной
фильтрации,
как адекватное каскадное описание динамики случайного
процесса в условиях неопределённости, способные на основании наблюдаемого
выборочного функционала y(t) случайного процесса со стационарными приращениями Y(t)
восстановить многомерную динамику его основной тенденции.
Применение динамических предикторных моделей
весьма эффективно в решении инженерных задач, таких как управление существенно
нелинейными объектами, объектами с запаздыванием, управление при неполной
информации о состоянии системы. В них используются конечно-разностные формы
описания динамических систем, реализуемые на современных компьютерах, в отличие
от дифференциальных уравнений, применяемых в теоретических исследованиях и
удобных при реализации на аналоговой технике.
Кроме каскадно-эволюционного подхода, на котором основаны ДПМ, для
синтеза моделей ДСП представляет интерес подход основанный на использовании
законов статистической взаимосвязи. Вызывает серьёзные возражения
обоснованность применения для этого ковариационных функций: ими нельзя
однозначно описать даже стационарный случайный процесс.
Во-первых, ковариационная функция предназначена
для оценки количественных характеристик только конкретно известного вида процесса.
Во-вторых, не даёт возможности ответить на
вопрос о его непрерывности. Классическими иллюстрациями этих двух возражений можно
считать две пары процессов с одинаковыми ковариационными функциями, как пуассоновский
и винеровский, а также телеграфный и Орнштейна-Уленбека, в которых первый –
дискретный, а второй – непрерывный.
В-третьих, если эти функции определяются с
ошибкой, например, при усреднении и центрировании, то результат сильно искажается,
поскольку математическое ожидание оценивается через среднее арифметическое, что
при нестационарности выборки нарушает требование однородности для этой операции.
В-четвёртых, и это главное, они не
содержат информации о динамических характеристиках исследуемых процессов и не
предназначены для изучения поведения фазовых состояний систем, а являются лишь
численными оценками статистической взаимосвязи между сечениями стационарного случайного
процесса.
Для определения характеристик случайных
процессов со стационарными приращениями, А.Н. Колмогоров ввёл [8] функции,
названные структурными, которые были исследованы его учениками
А.М. Ягломом, В.И. Татарским, А.Ф. Романенко и другими.
Показано, что частным случаем структурных функций являются ковариационные.
Вторая моментная функция приращений ДСП
![]() ,
,
называемая структурной функцией, характеризует интенсивность
флуктуаций случайных процессов. Для случайных процессов со стационарными
приращениями первого порядка соответствующая структурная функция имеет вид ![]() , а структурная функция, с учётом стационарности n-го приращения [5], соответственно
записывается как
, а структурная функция, с учётом стационарности n-го приращения [5], соответственно
записывается как
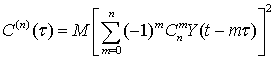 .
.
При оценивании характеристик
нестационарного случайного процесса необходимо учитывать его закономерности,
поскольку единственная возможность нахождения статистических характеристик
процесса по-прежнему заключается в усреднении по большому числу реализаций, получаемых
в одинаковых условиях. Такими возможностями обладают кросс-структурные функции [9]
![]() ,
,
определяющие статистическую взаимосвязь между
последовательными приращениями динамического процесса, как между случайными
процессами, но с учётом инерционности их характеристик. Такой структурный
показатель связывает последовательные приращения порядков s и u. При s = u и cs = du = 1 определяет качество каскадной фильтрации в
ДПМ, а при s = u = 0 и cs = du = 1 совпадает со структурной функцией.
Использованные литературные источники
1.
Kaladze V.A. Mathematical models of casual processes with stationary
increments and the non-uniform information dynamic processing: Monograph. –
Lorman, MS, USA: Science Book Publishing House, 2012. -136 p.
2.
Каладзе В.А. Алгоритмические
модели и структурные функции динамических случайных процессов/ В.А. Каладзе //
Системы управления и информационные технологии. – Москва-Воронеж, № 3 (41),
2010. – С. 4-7.
3.
Каладзе В.А.
Динамические случайные временные последовательности/ В.А. Каладзе // Междунар.
научно-техн. конференция «Информационные и управляющие системы». – Воронеж:
ВГТА, 2009. – С. 77-80.
4.
Колмогоров А.Н. Спираль
Винера и некоторые другие интересные кривые в гильбертовом пространстве/ А.Н.
Колмогоров // ДАН СССР 1940, т. 26, № 1. – С. 115-118.
5.
Яглом А.М.
Корреляционная теория процессов со случайными n-ми приращениями/ А.М. Яглом // Матем. сборник, 1955. Т.37. Вып.
1. – С. 79-85.
6.
Колмогоров А.Н. Кривые в
гильбертовом пространстве, инвариантные к однопараметрической группе движений/ А.Н.
Колмогоров // ДАН СССР, 1940, т. 26. – С. 6-9.
7.
Каладзе В.А.
Стохастические структуры динамических моделей: формализация динамического ядра /
В.А. Каладзе // Системы управления и информационные технологии. –
Москва-Воронеж, № 4 (38), 2009. – С. 12-15.
8.
Колмогоров А.Н.
Рассеяние энергии при локально изотропной турбулентности/ А.Н. Колмогоров //
ДАН СССР, 1941, № 32, № 1. – С. 19-21.
9.
Каладзе В.А., Ганцева
Е.А. Оценка взаимосвязи между последовательными приращениями динамического
случайного процесса. Материалы 12 междун. науч. конф. – Воронеж: ВГУ, 2012. –
С. 218-219.