Математика/5. Математическое моделирование

Жуаспаев Т.А.

Костанайский государственный университет имени А.Байтурсынова, Республика Казахстан

Априорные оценки для решения прямой задачи

Рассматривается следующая задача [1]:

, , (1)

, , (2)

. (3)

Будем искать обобщенный коэффициент теплообмена. Ось направлена вверх, начало координат находится на неизменном слое температуры почвы. Дополнительно задается измеренное значение температуры грунта на поверхности земли и температура воздуха тоже на поверхности земли. Рассмотрим частный случай, когда . То есть располагая величинами и требуется определить и . Здесь - измеренное значение температуры грунта на поверхности земли. Задача решается итерационным способом. Пусть – итерационный параметр. В этом случае определяются итерационными величинами ,

Рассмотрим, когда . В этом случае исходная дифференциальная задача записывается в виде

, (4)

(5)

. (6)

Умножим (4) на и интегрируем по от 0 до Н. После однократного интегрирования по частям по переменной имеем равенство

.

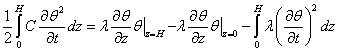Обозначим снова через . Тогда второй интеграл в правой части знака равенство превращается в нуль. Учитывается граничное условие (5). Предполагаем, что . В этих предположениях интегрируется полученное равенство по t от 0 до произвольных t. Тогда

.

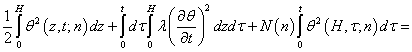
Применяя неравенство Коши выводим, что

.

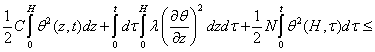
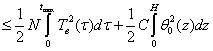Пусть

.

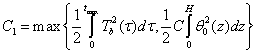Тогда

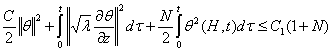. (7)

Литература

1. Rysbaiuly B. Newton’s method to solve the problem of heat transfer in the freezing soil. France, Paris, Pensee Journal, Volume 76, Issue 1, 261-275 pp.

2. Alemdar Hasanov Simultaneous determination of source terms in a linear parabolic problem from the final overdetermination: Weak solution approach. J. Mathematical Analysis and Applications. 330 (2007) 766–779 pp.

3. Rysbaiuly B.^, Baimankulov A. Development and justification of the method of calculation the capillary diffusion of the soil. Wulfenia Journal, Austria, Mar 2014, Volume 20, Issue 12, 483-500 pp.