УДК 519.712.1

ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ ЗАМКНУТОЙ СИСТЕМЫ УПРАВЛЕНИЯ ОБЪЕКТОМ С НЕТОЧНЫМИ ДАННЫМИ

Н.Р. Юничева

к. т.н., доцент, в.н.с.

Институт информационных и вычислительных технологий Республика Казахстан, г. Алматы

В статье представлена процедура исследования свойства асимптотической устойчивости замкнутой системы управления объектами с неточными данными на основе использования неравенств Брауэра, полученных ранее для оценки устойчивости точечных систем.

Развитие новых концепций и принципов построения интеллектуальных систем управления на современном этапе теории управления динамическими объектами, функционирующими в условиях неопределенности является актуальной задачей.

Системы управления современными техническими объектами, как правило, характеризуются большим числом параметров и взаимосвязей, настолько большим, что иногда невозможно решать такие задачи аналитически, и не всегда можно упростить задачу для проведения экспериментов.

Также неоднократно отмечалось, что большая часть систем автоматического управления функционирует в условиях параметрической неопределенности [1]. Однако многообразие особенностей этих неопределенностей не позволяет создать единую теорию анализа и синтеза таких систем [2]. О данных таких систем известно лишь то, что они принадлежат замкнутым конечным интервалам вещественной оси. Фактически, рассматривается задача управления спектром траекторий в фазовом пространстве, причем весь спектр должен обладать требуемыми динамическими свойствами.

Оказывается, что многие сложные управляемые объекты с интервальными неопределенностями можно достаточно адекватно описывать вышеуказанным способом.

Разработка концепций и принципов построения систем управления сложными динамическими объектами, функционирующими в условиях неопределенности актуальна для современного этапа развития теории автоматического управления. Решение таких задач осуществляется на основе аппарата интервального анализа, который является наиболее адекватным инструментом описания для объектов, функционирующих в условиях параметрической неопределенности [3].

С другой стороны, хорошо известно, что реальные технические объекты, функционируют в условиях параметрической неопределенности. Неопределенность подобного рода обусловлена наличием неконтролируемых возмущений, действующих на объекты управления, по причине незнания истинных значений параметров объекта управления из-за сложности технологического процесса, а иногда и непредсказуемым изменением их во времени. Почти во всех случаях вышеупомянутая параметрическая неопределенность характеризуется принадлежностью реальных значений параметров технического объекта некоторым интервалам, границы которых априорно известны. Их математические модели могут быть представлены системами интервальных дифференциальных или разностных уравнений с использованием правил и обозначений интервального анализа, а класс таких объектов управления принято называть интервально-заданными.

Таким образом, возникает задача управления и исследования динамики не единственного объекта, а семейства или множества объектов.

В предлагаемой статье решается задача исследования асимптотической устойчивости для интервальной замкнутой системы управления, математическая модель которой в пространстве состояний представляется формулой следующей формулой:

, (1)

где , — вещественная интервальная матрица замкнутой системы управления, — множества матриц, элементами которых являются вещественные интервалы ; - множества всех вещественных интервалов; - вектор состояний.

При этом желаемый интервальный характеристический полином определяется следующим образом:

, (2)

где - единичная матрица; - интервальные коэффициенты характеристического полинома замкнутой системы управления.

Как отмечалось выше, для исследования динамических свойств данной системы потребуется исследование динамических свойств целого семейства точечных систем.

Рассмотрим заданную матрицу замкнутой системы управления.

Пусть - точечная матрица такая, что . Для проведения дальнейших рассуждений воспользуемся следующими определениями:

Определение 1.

Интервальная матрица замкнутой системы управления вида (1) асимптотически устойчива, если асимптотически устойчивы все точечные матрицы .

Как известно [4] , характеристическое уравнение матрицы представляется следующим образом:

(3)

Тогда, для интервальной матрицы имеет следующее определение:

Определение 2.

Семейство характеристических уравнений для всех точечных матриц называется характеристическим уравнением нечеткой матрицы и формально записывается в следующем виде:

(4)

Предположим, что матрица асимптотически устойчива и все ее собственные значения локализованы в круге единичного радиуса в левой части плоскости комплексного переменного .

Решение задачи. Для получения матричного критерия асимптотической устойчивости воспользуемся известным дробно- линейным преобразованием [4] следующего вида:

(5)

Данное преобразование позволяет перевести круг заданного радиуса в левой части плоскости комплексного переменного , в единичный круг с центром в начале координат плоскости комплексного переменного . Значение из (3) подставим в (1), опуская промежуточные вычисления, получим:

(6)

где - преобразованная матрица, собственные значения которой расположены в круге единичного радиуса.

Как известно [4], если являются собственными значениями матрицы , то собственными значениями матрицы будут числа . Следовательно, если матрица замкнутой системы управления устойчива, то последовательное возведение матрицы в k–ую степень позволяет уменьшить абсолютную величину собственных значений , так как все локализованы внутри круга единичного радиуса и по модулю меньше единицы

(7)

Таким образом, для асимптотической устойчивости матрицы , необходимо и достаточно, чтобы неравенство (7) имело силу. Выполнимость необходимого и достаточного условия (7) устанавливается по факту убывания .

Окончательно критерий асимптотической устойчивости можно сформулировать следующим образом:

Для того, чтобы матрица замкнутой системы управления была асимптотически устойчива, необходимо и достаточно, чтобы преобразованная матрица стремилась к нулевой при .

Интервальным аналогом точечной матрицы является матрица следующего вида:

(8)

где .

Аналогично рассмотренному случаю для точечной матрицы сформулируем последовательность степеней матрицы .

Для асимптотической устойчивости интервальной матрицы замкнутой системы управления необходимо и достаточно, чтобы нижние и верхние границы всех элементов одновременно стремились к нулю.

Возникает вопрос, можно ли установить факт устойчивости без возведения преобразованной матрицы в степень?

Вследствие того, что возведение в степень матриц высоких порядков представляется трудоемкой процедурой, для установления факта асимптотической устойчивости возможно использование так называемых неравенств Брауэра.

Брауэр в своей работе [8] представил достаточные условия для случая, когда все собственные значения вещественной матрицы F лежат внутри круга единичного радиуса с центром в начале координат.

Для полученной выше вещественной матрицы преобразования F, определяются следующие числа

(9)

Согласно Брауэру, если F – квадратная матрица порядка n с вещественными элементами и если среди чисел хотя бы одно, например, и вместе с тем , кроме того, выполняется условие

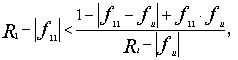(10)

для всех , для которых

, (11)

то все собственные значения матрицы F расположены внутри единичного круга с центром в начале координат.

Доказательство этой теоремы представлено в работе [5].

Если все неравенства Брауэра выполняются, то можно утверждать, что собственные значения преобразованной матрицы коэффициентов F лежат внутри круга единичного радиуса с центром в начале координат и система асимптотически устойчива.

Если хотя бы одно из неравенств Брауэра не выполняется, вопрос об устойчивости должен быть исследован дополнительно путем изучения последовательных степеней матриц .

В предлагаемой работе получено развитие методики Брауэра на случай интервальных матриц.

Для этого введем в рассмотрение вещественную матрицу с элементами :

(12)

Тогда, выражение (9) представится следующим образом:

(13)

А условие (10) приобретает вид:

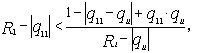(14)

Если все неравенства Брауэра выполняются, то можно утверждать, что все собственные значения преобразованной интервальной матрицы коэффициентов лежат внутри круга единичного радиуса с центром в начале координат и система асимптотически устойчива.

Если хотя бы одно из неравенств Брауэра не выполняется, то вопрос устойчивости возможно исследовать дополнительно путем изучения последовательных степеней матриц **…., .

Данная процедура подробно рассмотрена в [5].

Таким образом, применение неравенств Брауэра позволяет получить достаточное условие устойчивости замкнутой системы управления.

Также при помощи неравенств Брауэра оказалось возможным установить факт устойчивости без возведения преобразованной матрицы в степень.

А использование методов локализации позволяет указать более точное месторасположение собственных значений матрицы замкнутой системы управления, что является немаловажным фактором установления такого динамического свойства как асимптотическая устойчивость, особенно для сложных объектов, имеющих большую размерность и функционирующих в нечеткой среде.

Процедура вычисления радиуса , внутри которого локализованы собственные значения матрицы замкнутой системы управления, осуществлена на основе обобщения результатов Гершгорина С.А [6] на случай интервальной матрицы и представлена в статье [7].

Список литературы

1. Юничева Н.Р. Параметрический синтез управляющих воздействий. // Вестник КазНУ им. Аль-Фараби, № 4(59), с.117-120, 2008 г.

2. Ярушкина Н.Г. Основы теории нечетких и гибридных систем. Учебное пособие. Финансы и статистика, 2004.- 320c.

3. Шокин Ю.И. Интервальный анализ. Новосибирск.: Наука, Сиб.отд., 1981. 107 с.

4. Чернецкий В.И., Дидук Г.А., Потапенко А.А. Математические методы и алгоритмы исследования САУ. Л.: Энергия, 1970. -375 с.

5. Юничева Н.Р. Исследование динамических свойств интервальных замкнутых систем управления // Вестник Национальной инженерной академии РК, №2(20), 2006.C.32-37.

6. Гершгорин С.А. Об ограничении собственных значений матрицы. Изд. АН СССР, № 7, 1951.

7. Юничева Н.Р., Юничева Р.Р. Процедура вычисления радиуса локализации собственных значений интервальной матрицы // Труды Международной научно-практической конференции «Актуальные вопросы современной информатики» Коломна, 2011, -Т.№2. –С.154-156.

8. Brauer A. Matrices with all their characteristic roots in the interior of the unit circle. J. Elisha Mitchell Sec. Soc., 68 (1972), 180-185.