Применение подхода Филлипса к вопросу экономической стабилизации при обучении студентов

Детушев Иван Васильевич

Курский государственный университет, Россия

Применение подхода Филлипса к вопросу экономической стабилизации при обучении студентов – экономистов дифференциальным уравнениям.

В статье рассматривается применение задач с прикладным экономическим содержанием при обучении студентов – экономистов дифференциальным уравнениям на примере подхода Филлипса к вопросу экономической стабилизации.

Ключевые слова: дифференциальные уравнения, подход Филлипса, студенты- экономисты, задачи с прикладным экономическим содержанием.

Математика – это наука, в которой изучаются количественные соотношения реальности. Для студентов экономических специальностей вузов математика является не только мощным средством решения прикладных экономических задач, но и элементом общей культуры. Современным экономистам довольно часто приходится пользоваться сложным математическим аппаратом для анализа различных задач, характерных для сферы экономики. Поэтому математическое образование студентов – экономистов нужно рассматривать как одну из важнейших составляющих фундаментальной подготовки экономистов, маркетологов, управленцев.

Для будущих экономистов математика является инструментом анализа, организации и управления. Поэтому при обучении будущих экономистов математике особое внимание нужно уделять повышению уровня их фундаментальной математической подготовки с усилением её прикладной экономической направленности. Одним из возможных путей достижения глубокой фундаментальной математической подготовки студентов – экономистов в сочетании с прикладной направленностью их обучения являются математические задачи с прикладным экономическим содержанием. О ценности применения данного подхода к обучению математике будущих экономистов нами подробно рассказано в работах [1,2]. Остановимся на преподавании дифференциальных уравнений будущим экономистам.

Использование задач с прикладным экономическим содержанием при обучении студентов – экономистов методам решения дифференциальных уравнений позволяет сделать излагаемый математический материал более наглядным и доступным для понимания учащихся, а также сподвигнуть их к поиску новых математических знаний. Дифференциальные уравнения – довольно часто применяемый аппарат для решения многих экономических задач. Так, например, дифференциальные уравнения применяются для моделирования проблемы инфляции, государственного долга, экономического роста, безработицы, взаимосвязей денежного и реального рынков и т.д.

По мнению Ж.С. Сулейменова: «Прикладная направленность дифференциальных уравнений отводит задачам ключевое место. Любой теоретический материал можно предварять задачами прикладного характера, приводящими к тем дифференциальным уравнениям, которые предстоит изучить в данном разделе, т. е. обосновать мотивацию изучения этого раздела. Поэтому задачный материал используется не только как цель реализации теории на практике, но и как средство обучения» [4]. На наш взгляд, использование задач с прикладным экономическим содержанием при изучении студентами – экономистами раздела «Дифференциальные уравнения» приведет к:

- повышению внимания студентов к изучению дифференциальных уравнений и их систем;

- глубокому усвоению и запоминанию применяемых в задачах экономических понятий;

- раскрытию перед учащимися применимости аппарата дифференциальных уравнений в экономике.

На примере подхода Филлипса к вопросу экономической стабилизации, покажем возможность применения задач с прикладным экономическим содержанием при обучении студентов – экономистов дифференциальным уравнениям.

Как известно, существует достаточно много вариантов политики экономической стабилизации, которые может применить правительство для постепенного уравновешивания колебаний спроса и предложения различной продукции. Филлипсом были выделены три типа политики экономической стабилизации:

1) Политика пропорциональной экономической стабилизации. В этом случае планируемый уровень государственных расходов (правительственный спрос) будет иметь вид: , где - объем национального дохода (объем выпуска продукции), - заданная величина. Заметим, что в этом случае при падении выпуска продукции ниже желаемого уровня (), предъявляемый правительством спрос пропорционален сокращению производства.

2) Политика дифференциальной стабилизации. В этом случае правительственный спрос равен: , где - объем национального дохода (объем выпуска продукции), - заданная величина. Заметим, что в этом случае связан не с дефицитом продукции, а со скоростью изменения национального дохода .

3) Политика интегральной стабилизации. В этом случае правительственный спрос равен: , где - объем национального дохода (объем выпуска продукции), - заданная величина. Заметим, что в данном случае правительственный спрос пропорционален накапливающемуся дефициту национального дохода.

Рассмотрим подход Филлипса подробнее.

Пусть - планируемый уровень государственных расходов, - реальный уровень государственных расходов, тогда для улучшения экономической стабилизации нужно минимизировать разность . Введем обозначения: - коэффициент реакции, то есть коэффициент, показывающий скорость принятия правительством решений. Тогда решение о государственных расходах можно определить как решение линейного дифференциального уравнения первого порядка: , где - один из трёх предложенных вариантов экономической стабилизации, который вводится с целью достижения равновесия спроса и национального дохода.

В случае модели Филлипса только с мультипликатором, совокупный спрос , с учетом спроса со стороны государства, примет вид: (*), где - склонность к потреблению, - потребление, - автономные инвестиции. Объем национального дохода (потребление) в этом случае будет задаваться уравнением:

(**).

Студентам – экономистам на практических занятиях по высшей математике можно предложить найти математическую модель политики экономической стабилизации, а затем, применив один из трёх базовый вариантов политики государственных расходов, выявить к какому результату приведет выбранная политика. Приведем пример нахождения данной модели:

Подставим уравнение (*) в уравнение (**), получим: , где - склонность к сбережениям, (инвестиции полагаем неизвестными)

Теперь продифференцируем уравнение (*) по переменной , получим:

(***). Сложив уравнение (***) с уравнение (*), умноженным на , получим:

, затем решая систему:

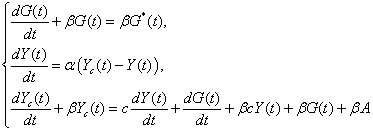
получим дифференциальное уравнение следующего вида:

. Анализ этого уравнения даст ответ на поставленную задачу.

Таким образом, применение подхода Филлипса к вопросу экономической стабилизации при обучении студентов – экономистов дифференциальным уравнениям позволяет будущим экономистам увидеть связь математики и экономики, что активизирует познавательную активность обучающихся студентов по математике.

Литература:

Детушев, И.В. Прикладная направленность курса «Математика» на экономических факультетах университетов [Текст] / И.В. Детушев // Теоретические и практические проблемы развития современной науки: сборник материалов III Международной научно – практической конференции. – Махачкала: Изд-во НИЦ «Апробация», 2013. – С. 153-155.
Детушев, И.В. Особенности методики преподавания математики на экономических факультетах вузов [Текст] / И.В. Детушев, В.П. Добрица // Актуальные проблемы и перспективы в преподавании математики: сб. научных статей Международной научно – практической конференции. – Курск: Изд-во Юго - Запад. гос. ун-та, 2010. – С. 60-64.
Минюк, С.А. Дифференциальные уравнения и экономические модели [Текст] / Н.С. Берёзкина, С.А. Минюк. – Минск: «Вышэйшая школа», 2007. – 142 с.

4. Сулейменов, Ж.С. Методическая система обучения дифференциальным уравнениям студентов физико – математических факультетов университета [Текст]: дисс. д-ра пед. наук: 13.00.02/ Ж.С. Сулейменов. – Алматы, 2003. – 257 с.