Integral assessment of the effects of electric field
on the
speed of the drying process
Nikolaev N.S.
Dr. Ph. Of
Technical Sciences, Professor,
Burlev M.Ya.
Dr. Ph. Of
Technical Sciences, Academic IAR,
Uruypin M.A.
Dr. Ph. Of Technical Sciences,
Moscow State
University of Food Industry,
Russian Federation
Introduction. The results of experimental
research and mathematical modeling of the process of drying of skim milk in a
thin layer with the application of an electric field. Implemented an integrated
assessment of the impact of the electric field at the speed of the drying
process. Graphically shows the dependence of the electric field effect on the
drying process of its key features.
Keywords: skimmed milk, drum (roller)
dryer, mathematical modelling, electrical field, convective drying, drying in a
thin layer, intensification
Many products to dehydration are the
convective drying in a thin layer. To do this, often use drum (rolling) dryer.
The efficiency of the drying process in a drum dryer is associated largely with
the processing time. In addition, it is directly related to, including, and the
size of the drum [1]. In this regard, the intensification of the process of
drying of skim milk in a thin layer is an urgent task that will reduce the size
of equipment, reduce processing time and thus reduce capital investment and
increase energy efficiency. To accomplish this, used the influence of electric
field [2].
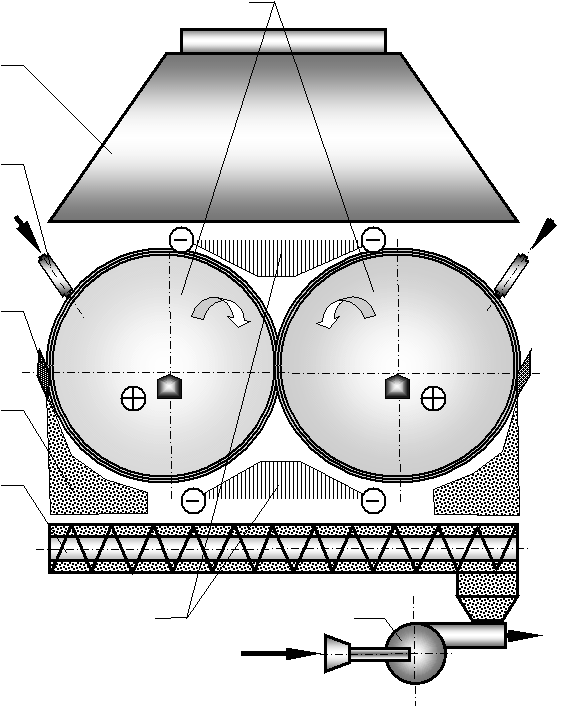
Figure of convection drying process in
a thin layer with the electric field presented in Fig. 1.
6
5
4
3
2
1
7 8
Fig. 1. Drum (roller) dryer milk using an electric
field:
1 – screw conveyor; 2 – product (skim milk); 3 –
scraper; 4 – nozzle;
5 – extractor hood; 6 – drums; 7 – electrodes; 8 – pneumatic
transport
Method of Integral assessment:
Remove
moisture under the action of the temperature field.
To
describe the first period of drying mass transfer (constant speed), can use a
known mass linear equation:
-dW/dτ = const = β (Wequil.
– Wavrg.) (1)
W – the moisture content of the material,
kg/kg;
Wequil – equilibrium moisture content of the material,
kg/kg;
Wavrg. – the average amount of body moisture content
material, kg/kg;
τ – time, sec;
β – the mass transfer coefficient, 1/sec.
To
describe a mass transfer of the second period (the period of the falling speed)
using diffusion equation (2-nd Fick's law):
∂W/∂τ
= D (∂2W/∂x2 + ∂2W/∂y2 + ∂2W/∂z2) (2)
D - the
diffusion coefficient, which takes into account a number of internal mass
transfer, m2/sec;
x, y, z – spatial
coordinates, m.
It was for drying
layer of skim milk on the substrate assumed, that is a lot smaller than the
thickness of the substrate, and physical properties of the material are constant
throughout the substrate. In this case, from a three-dimensional spatial
diffusion equation can be one-dimensional equation:
∂W/∂τ
= D (∂2W/∂h2) (3)
h – is the only axis-height in a layer on
a substrate, m.
The initial
condition:
τ = 0, 0
<h <H, W = WB,
H – layer thickness, m;
WB – the initial moisture content of
the material, kg/kg.
Boundary conditions:
τ ≥ 0, h = 0, ∂W/∂h = 0, τ →
∞, h = H, W = Wequil ,
The
exact analytical solution of this equation generally get fails, but using
numerical methods [3], you will get a solution for any given option.
Family
of functions W (h) moisture distribution in the thickness of the thin layer at
regular intervals is shown in the following graph (τ = 0, the initial moisture content W (h) = WB
= const):
 Wí,%
Wí,%
|
100 |
|
|
|
|
|
|
|
|
|
|
|
75 |
|
|
|
|
|
|
|
|
|
|
|
50 |
|
|
|
|
|
|
|
|
|
|
|
25 |
|
|
|
|
|
|
|
|
|
|
|
10 Wequil |
|
|
|
|
|
|
|
|
|
|
0 10 20 30 40 50 60 70 80 90 100 h/H/%
Figure. 2. Family of
graphs the distribution of moisture content W in thickness of a thin layer of
skim milk on a substrate at regular intervals.
Remove
moisture under the action of the electric field.
In order to get closer to the understanding of the influence
of electric fields on the process of removing moisture from the product and to
quantify this impact in the form of a supplementary member of the equation
obtained experimental data have been processed, are listed below.
Focused on the experimental data of drying thin layer of
skim milk on the substrate.
Variants:
À0 – without electric impact
À1 - frequency of impulses f1 = 150 Hertz, duty
cycle Q = 3
À2 - frequency of impulses f2 = 200 Hertz, duty
cycle Q = 3
À3 - frequency of impulses f3 = 300 Hertz, duty
cycle Q = 3
À4 - frequency of impulses f4 = 400 Hertz, duty
cycle Q = 3
Â1 - duty cycle Q1 = 2, frequency of impulses f = 200 Hertz
Â2 - duty cycle Q2 = 3, frequency of impulses f = 200 Hertz
Â3 - duty cycle Q3 = 5, frequency of impulses f = 200 Hertz
Â4 - duty cycle Q4 = 10, frequency of
impulses f = 200 Hertz
Voltage
(amplitude) U = 600 Volt
Note: Variants À2 and Â2 are the same and are for
illustration purposes only.
Results and discussion.
Table. 1.
Drying speed-changes per 60 sec. mass fraction in drying thin layer of skim
milk on a W [%/60 sec]
|
60 |
120 |
180 |
240 |
300 |
360 |
420 |
480 |
540 |
600 |
660 |
720 |
780 |
840 |
900 |
960 |
1020 |
1080 |
Variants. |
|
18 |
11 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
8 |
8 |
7 |
7 |
6 |
5 |
4 |
2 |
1 |
À0 |
|
18 |
11 |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
9 |
8 |
7 |
5 |
4 |
4 |
2 |
2 |
0 |
À1 |
|
20 |
25 |
18 |
22 |
21 |
11 |
8 |
10 |
2 |
3 |
0 |
|
|
|
|
|
|
|
À2 |
|
19 |
12 |
9 |
9 |
10 |
9 |
10 |
10 |
10 |
9 |
8 |
8 |
4 |
5 |
4 |
2 |
2 |
0 |
À3 |
|
18 |
12 |
10 |
11 |
10 |
9 |
9 |
9 |
9 |
8 |
10 |
8 |
7 |
5 |
2 |
2 |
1 |
0 |
À4 |
|
20 |
12 |
16 |
12 |
16 |
17 |
15 |
10 |
7 |
6 |
3 |
4 |
1 |
1 |
0 |
|
|
|
Â1 |
|
20 |
25 |
18 |
22 |
21 |
11 |
8 |
10 |
2 |
3 |
0 |
|
|
|
|
|
|
|
Â2 |
|
18 |
17 |
20 |
17 |
19 |
16 |
13 |
3 |
6 |
3 |
2 |
2 |
2 |
1 |
1 |
0 |
|
|
Â3 |
|
18 |
12 |
12 |
11 |
11 |
11 |
11 |
11 |
10 |
9 |
7 |
4 |
5 |
3 |
2 |
3 |
0 |
|
Â4 |
Table. 2. Change the speed of drying thin layer of skim milk on a W
[%/60 sec] due to the electrical effect.
|
. |
60 |
120 |
180 |
240 |
300 |
360 |
420 |
480 |
540 |
600 |
660 |
720 |
780 |
840 |
900 |
960 |
1020 |
The average value of [%/60sec/600V] |
Interval comparison [sec.] |
The value of the argument function |
|
À1-À0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
-2 |
-1 |
-2 |
0 |
1,0 |
180-600 |
f
= 150 Ãö |
|
À2-À0 |
2 |
14 |
9 |
13 |
12 |
2 |
-1 |
1 |
-7 |
-5 |
|
|
|
|
|
|
|
10,0 |
120-360 |
f
= 200 Ãö |
|
À3-À0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
-3 |
-1 |
-1 |
-2 |
0 |
0,6 |
180-720 |
f
= 300 Ãö |
|
À4-À0 |
0 |
1 |
1 |
2 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
-1 |
-3 |
-2 |
-1 |
0,5 |
180-720 |
f
= 400 Ãö |
|
Â1-À0 |
2 |
1 |
7 |
3 |
7 |
8 |
6 |
1 |
-2 |
-2 |
-5 |
-5 |
-3 |
-6 |
|
|
|
6,2 |
180-420 |
Q
= 2 |
|
Â2-À0 |
2 |
14 |
9 |
13 |
12 |
2 |
-1 |
1 |
-7 |
-5 |
|
|
|
|
|
|
|
10,0 |
120-360 |
Q
= 3 |
|
Â3-À0 |
0 |
6 |
11 |
8 |
10 |
7 |
4 |
-6 |
-3 |
-5 |
-6 |
-5 |
-5 |
-5 |
-4 |
|
|
7,7 |
120-420 |
Q
= 5 |
|
Â4-À0 |
0 |
1 |
3 |
2 |
2 |
2 |
2 |
2 |
1 |
1 |
-1 |
-3 |
-2 |
-3 |
-3 |
-1 |
|
1,8 |
120-600 |
Q
= 10 |
Analysis of
experimental data has shown that in the investigated range during constant
speed the drying effect of the electric field at a rate of close to zero. In
this range, the process of evaporation of moisture from the free product is a
determining and little depends on the influence of the electrical impulse
actions.
For the second
period of drying, the situation is different. From the table. 2 shows that the
difference between the speeds of almost constant drying. Within the limits of
the physical process, described by Fick's equation, which is in the table. 3
designated as "Interval comparison". A simple (not depending from W)
can describe the effect an additional member on the right side of the equation
for the derivative W by time:
∂W/∂τ = D (∂2W/∂h2) – kï(f, Q) U (3)
W – moisture content, %
t – time, sec;
h – height in a layer of dried material, m;
D – coefficient
of molecular diffusion, m2/sec;
U –
voltage (amplitude), Volts;
kn –
coefficient of influence of electric field on drying process of a flat layer,
which is a function of many parameters, including:
f – frequency of impulses Hertz;
Q – duty cycle.
Table. 3. The coefficient kn in units of [1/sec/V] for drying of skim milk on the substrate:
|
Q \ f, Hertz |
150 |
200 |
300 |
400 |
|
2 |
|
1,7 10-6 |
|
|
|
3 |
0,28 10-6 |
2,8 10-6 |
0,16 10-6 |
0,14 10-6 |
|
5 |
|
2,1 10-6 |
|
|
|
10 |
|
0,5 10-6 |
|
|
Two-dimensional
surface coefficient kn for drying of milk on the substrate
as a function of frequency f and duty cycle Q is shown in Fig. 3.
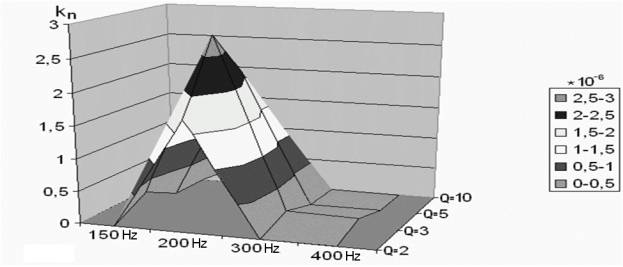
Fig. 3. Dependence of the coefficient kn
from frequency f and duty cycle Q.
Modelling of drying process in a thin
layer with the electric field can be the basis for its intensification in a
drum dryer and the results as a basis for the development of more efficient
equipment.
Literature.
1. Ilyukhin V.V., Burlev
M.Ya., Zhukavets E.V. / Drying milk using electric fields // Dairy industry – 2011.
– ¹ 8. - P. 11 - 12.
2. Burlev, M. Ya. Use
of the drying with influence electricity potential in medicine and
pharmaceutics industry // Biomedical and Biosocial Anthropology official
Journal of the International Academy. National Pyrogov Memorial Medical
University. Vinnitsa, Ukraine. December 2011. – ¹ 17. – P. 267 – 269.
3. Guzev O.Yu. "Development
of a high-tech process of fluidized bed dryer with heat pump”. Diss. of Ph. Tech. of Sciences.
M. – 2008.
148
pages.