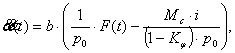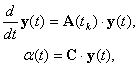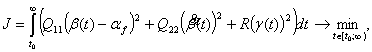Лазарева Е.В., канд. техн. наук, Осинский Ю.А., доц., Копп В.Я., д-р техн. наук, проф., Лазарев В.Б., стар. препод.

Севастопольский национальный технический университет

ул. Университетская, 33, Севастополь, Украина 99053

e-mail: v_kopp@mail.ru

Методы разработки САУ колебательным шаговым пневмоприводом поворотного действия

Рассматриваются различия между двумя методами разработки систем автоматического управления углом поворота выходного элемента колебательного шагового пневмопривода поворотного действия.

Ключевые слова: динамические характеристики, колебательный шаговый пневмопривод, системы управления, программное управление

1. Объект исследования.

Колебательные шаговые пневмоприводы поворотного (КШПП) действия имеют ряд преимуществ перед другими типами пневмоприводов, осуществляющих позиционирование в большом числе фиксированных положений, что обусловливает возможность их широкого использования в различных устройствах. Их несомненным преимуществом является возможность осуществления контурного управления при необходимости перемещения исполнительного органа по заданной траектории с заданной скоростью.

Цель исследования – создание способа разработки системы автоматического управления (САУ) поворотом ведомого элемента посредством включения \ выключения пневмоприводов.

Дифференциальное уравнение, описывающее изменение угла поворота ведущего элемента, имеет вид [1, 2]:

(1)

где a(t) – угол смещения ведущего элемента; – результирующее воздействие, оказываемое на ведущий элемент, которое определяется тангенциальной составляющей суммы управляющих воздействий, создаваемых мембранными пневмоприводами, и суммарной силой трения, которая зависит от нормальной составляющей ; – установившееся значение силового воздействия, которое оказывает мембранный пневмопривод в режиме «включено»; 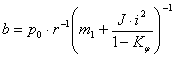; r – радиус окружности колебаний ведущего элемента; – масса ведущего элемента; момент инерции системы; – момент инерции ведомого элемента; – масса нагрузки; – радиус траектории нагрузки; – коэффициент клиновой передачи «ведущий элемент – ведомый элемент»; – коэффициент; – момент сопротивления, действующий на выходном валу; – диаметр окружности колебаний ведущего элемента, причем – модуль зацепления; – диаметр ведущего элемента; – диаметр ведомого элемента; – коэффициент трения.

Рассматривалась динамика КШПП с мембранными пневмоприводами, расположенными под углом 45° друг относительно друга. Для данного случая управления, в соответствии с [2], суммарная сила:

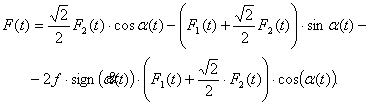
где и определяют силу воздействий 1‑ого и 2‑ого пневмоприводов, соответственно; – коэффициент трения. Переключение пневмоприводов может осуществляться только в определенные моменты , из дискретного множества зависящего от частоты срабатывания пневмоприводов и определяемой их техническими возможностями ( ).

Управление, оказываемое l‑ым пневмоприводом на интервале времени определяется соотношением:

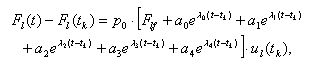(2)

где – величина, отражающая осуществление в данный момент времени силового воздействия l‑ым пневмоприводом, (“0” – привод отключен; “1” – включен); – коэффициент, принимающий одно из двух значений: , если пневмопривод работает на опорожнение, и , если пневмопривод работает на наполнение; – коэффициенты (в общем случае – комплексно‑сопряженные) разложения функции управления по экспоненциальным функциям с соответствующими показателями , которые также могут принимать два варианта значений, в зависимости от того на опорожнение или на наполнение работает l‑ый пневмопривод.

Поскольку определение точного значения весьма затруднительно то при построении закона управления допустимо учитывать только сам факт включения \ выключения l‑ого пневмопривода.

Динамика исходной нелинейной системы (1) после линеаризации достаточно адекватно описывается линейным дифференциальным уравнением в нормальной форме Коши, с коэффициентами, имеющими постоянное значение на интервалах :

(3)

где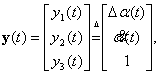
; .

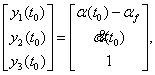
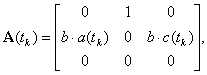
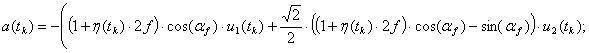
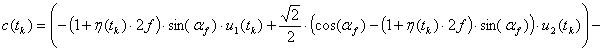
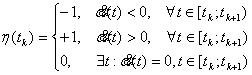2. Алгоритм программного управления. В задаче конструирования требуется произвести поворот ведущего элемента из начального положения в конечное , осуществив остановку в конечной позиции (т.е. ,). Важная отличительная черта исследуемой САУ состоит в необходимости реализовать управление путем выбора на дискретном множестве моментов времени величин двух переменных и из множества значений .

Предлагается два следующих подхода к решению задачи.

Первый подход (приближение переменных к конечным значениям) [3].

Управление пневмоприводами осуществляется так, чтобы на каждом из дискретных интервалов положение ведущего элемента максимально приближалось к требуемому конечному:

то есть обеспечивалась минимизация ошибки по положению:

Для реализации предложенного метода следует определить все допустимые значения управления и соответствующие им формулы для вычисления ошибки управления . Расчет управления в момент переключения заключается в выборе из всех возможных вариантов управления вариант соответствующей наименьшей ошибке.

В зависимости от варианта управления () и изменения на интервале скорости (), матрица может принимать одно из десяти значений :

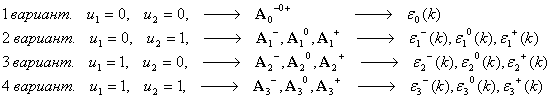
Этим десяти вариантам матрицы соответствуют десять матриц перехода системы и четыре ошибки (, , , ):

(4)

Соотношения (4) позволяют по данным, поступающим с датчиков положения и скорости ведущего элемента, определить четыре варианта оценки ошибки , соответствующие различным вариантам управления. Посчитав их все, следует выбрать управление, соответствующее наименьшей ошибке.

Этот метод можно усовершенствовать, получив значительное повышение точности работы САУ. Для этого предлагаем использовать методы теории автоматического управления. Очевидно, что осуществить изменение сил и во времени так, чтобы закон изменения соответствовал линейному закону обратной связи, физически невозможно. Однако, представляется возможным максимально приблизить нелинейное функционирование управляющих механизмов к желаемому линейному.

Второй подход (использование абстрактной САУ)

а) Осуществляется проектирование абстрактной идеальной линейной САУ вида

(5)

где β – идеальное значение угла смещения ведущего элемента, – идеальное управление, соответствующее желаемому линейному закону:

(6)

Для выбора матриц , определяющих закон управления (6) абстрактной САУ (5), может использоваться любой из известных методов проектирования САУ. В данной работе разработка абстрактной САУ осуществлялась методом линейно-квадратической оптимизации, обеспечивающим минимальное значение функционала качества:

(7)

где , , – скалярные числа, определяющие вес соответствующих переменных в функционале. Управление (6), соответствующее минимальному значению функционала качества определяется соотношениями:

где P – решение алгебраического уравнения Риккати второго порядка:

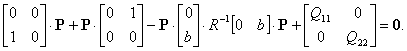
б) Управление пневмоприводами осуществляется так, чтобы функционирование линейного приближения реальной нелинейной САУ на каждом интервале времени максимально совпадало с функционированием САУ (5):

при идентичных начальных условиях:

Обеспечивается минимизация различий между траекториями систем (1) и (5) в дискретные моменты времени:

Таким образом, основное отличие второго подхода от первого состоит в том, что выбор управления на каждом шаге осуществляется сравнением текущего состояния САУ не с требуемым конечным состоянием, а сравнением с состоянием идеальной линейной САУ.

Также как и в первом подходе, в зависимости от управления и изменения на интервале скорости матрица, может принимать одно из десяти значений , которым соответствуют десять матриц . Абстрактной САУ, в свою очередь, соответствует матрица перехода , определяемая матрицами обратной связи и :

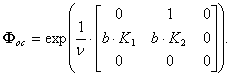
Условие выбора управления в момент времени сводится к выбору управления, соответствующего наименьшей из четырех ошибок (, , , ), определяемых по формулам:

(8)

Так же как и соотношения (4) , соотношения (8) отображают четыре варианта функциональной зависимости оценок ошибок , соответствующих различным вариантам управления.

3. Пример моделирования динамики колебательного шагового пневмопривода поворотного действия с программным управлением. Исследовался привод с параметрами: ; ; ; ; ; ; ; ; ; .

Пневматический привод, исходя из его динамики, представлялся звеном, характеризующимся параметрами , и , (). Параметры , выбирались на основании идентификации указанного объекта, исходя из кривой переходного процесса изменения давления в его полости. Параметры работы пневмопривода, работающего на наполнение: , , , , , , а на опорожнение: , , , , , .

При реализации второго подхода методом линейно‑квадратической оптимизации спроектирована идеальная САУ, соответствующая минимальному значению критерия качества (7) с коэффициентами ; ; .

Результаты моделирования динамики КШПП представлены на рисунке 1.

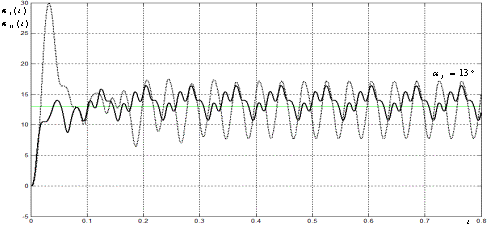
Рисунок 1— Результаты моделирования динамики КШПП: изменение угла поворота ведущего элемента при управлении двумя подходами: « - - » – первый способ управления; « – » – второй способ управления.

Выводы. Результаты исследования наглядно доказывают возможность осуществления позиционирования в произвольной точке за счет введения обратной связи. Причем, использование оптимального регулятора, построенного на принципах второго метода управления, позволяет уменьшить размах колебаний в конечной позиции на 15-25 % по сравнению с колебаниями, получаемыми при управлении первым методом.

В дальнейшем предполагается исследовать поведение КШПП в других режимах работы и с управлением, в котором принимают участие более двух мембранных приводов.

Литература

1. Копп В.Я. Пневматические модульные манипуляторы в сборочном производстве /В.Я. Копп //Машиностроительное производство. Сер. Автоматизация производства, гибкие производственные системы, робототехника. – М.: ВНИИТУЭМР, 1989. - Вып. 1 – С. 52.

2. Копп В.Я. Колебательные шаговые пневмоприводы /В.Я. Копп, Ю.А. Осинский, В.В. Поливцев //Оптимизация производственных процессов: Сб. научн. тр. – Севастополь, 2007. – Вып. 10. – С. 15 – 20.

3. Осинский Ю.А. Цифровая система автоматического управления (САУ) колебательным шаговым пневмоприводом поворотного действия / Ю.А. Осинский, В.Я. Копп, Е.В. Лазарева, В.О. Филиппович // Системные технологии. – Днепропетровск, 2011. 3(74).– С. 94 – 102.