Технические науки/ 2. Механика

К.т.н. Мюллер О.Д.

Северный (Арктический) Федеральный Университет, Россия

               ОСНОВЫ ТЕОРИИ ГИДРОПЛЕНОЧНОГО НАСОСА

         Работа выполнена в Северном (Арктическом) федеральном университете имени М.В. Ломоносова – головной исполнитель НИОКТР «Освоение высокотехнологичного мелкосерийного производства наукоемкой продукции – отечественных импорто-замещающих движительно-рулевых колонок и их компонентов для судов ледового класса» – при финансовой поддержке Министерства образования и науки РФ в рамках Постановления Правительства РФ № 218 от 9 апреля 2010 г.

        Выполнены теоретические исследования по расчету подачи и напорной характеристики  объемного насоса для перекачки вязких жидкостей, принцип действия которого основан на ламинарном течении жидкости в тонком клиновом зазоре.

Ключевые слова: объемный насос, ламинарное течение, гидравлический клин, напор насоса, напорная характеристика.

В настоящее время все насосы принципиально делятся на два класса по принципу подвода энергии к перекачиваемой жидкости. Динамические насосы, в которых подвод энергии осуществляется за счет увеличения кинетической энергии жидкости в относительном движении в межлопастных каналах рабочего колеса и объемные, в которых подвод энергии осуществляется за счет вытеснения жидкости вытеснителем (поршень, зубчатое колесо, винт и т.п.). Во всех этих насосах подача насоса носит в той или иной степени пульсационный характер.

Гидропленочные насосы принципиально отличаются от указанных выше. В них отсутствуют рабочие колеса  и вытеснители, а подвод энергии к жидкости осуществляется за счет ламинарного течения жидкости в тонком клиновом зазоре, у которого одна из стенок подвижна. Принципиальная схема одного из вариантов такого насоса представлена на рис. 1.

Насос состоит из комплекта неподвижных секторных дисков 2, между которыми установлены подвижные плоские диски 1. Подвижные диски 1 насажены на вал 3, относительно которого могут перемещаться в осевом направлении. Через вал 3 вращение от двигателя передается дискам 1.

 

 

 

 

 

 

 

 

 

 


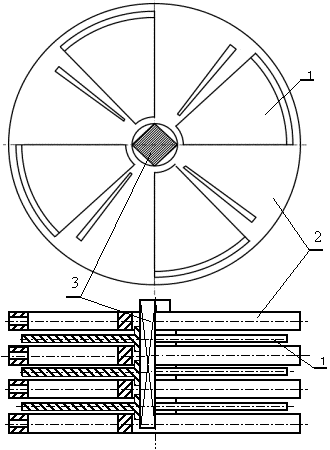
Рисунок 1 – Гидропленочный насос. 1 – вращающийся диск; 2 – неподвижный диск; 3 – вал.

Неподвижные диски 2 выполнены также плоскими и имеют вырезы в форме центральных секторов. Верхние и нижние поверхности дисков 2 имеют скос в сторону вращения подвижных дисков 1, образуя тем самым клиновой зазор между поверхностью вращающегося диска и неподвижной поверхностью сектора, толщина которого много меньше 1мм. В секторе выполнена радиальная сквозная прорезь, во внешней торцевой поверхности которой имеется отверстия для отвода жидкости (система сбора перекачиваемой жидкости и ее отвода для решения поставленной задачи не имеют принципиального значения и не показаны).

Принцип работы данного насоса заключается в следующем. Плоские диски приводятся во вращение, при этом за счет прилипания слоев жидкости к поверхности вращающегося диска (скорость жидкости на стенке рана 0) жидкость из межсекторного пространства затягивается в клиновой зазор между сектором неподвижного диска и подвижным диском. Так как  толщина зазора очень мала, то течение жидкости ламинарное (Re<<2300). По мере движения жидкости к выходу из клинового зазора давление жидкости нарастает [1]. При течении жидкости в районе радиальной прорези часть жидкости через нее и боковое отверстие поступает в напорный трубопровод, а остальная жидкость продолжает течение в клиновом зазоре до выхода из под подушки.

Цель настоящего исследования является разработка теоретических основ расчета гидропленочного насоса.

1.     Теоретическая часть.

Напорная характеристика гидропленочного насоса.

Для составления математической модели гидропленочного насоса воспользуемся основами теории упорного подшипника скольжения [1, 2]. 

Из теории расчета движения жидкости в плоском клиновом зазоре известно, что распределение давления жидкости по длине гидравлического клина, образованного подвижной поверхностью, движущейся со скоростью U, и неподвижной поверхностью при текущей  толщине клинового зазора h, можно определить по зависимости:

где: динамическая вязкость жидкости,

       сечение, в котором .

Данное дифференциальное уравнение используем для определения основных параметров гидропленочного насоса.   Рассмотрим один из секторов гидропленочного насоса, схема которого представлена на рисунке 2.

 

 

 

 


 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

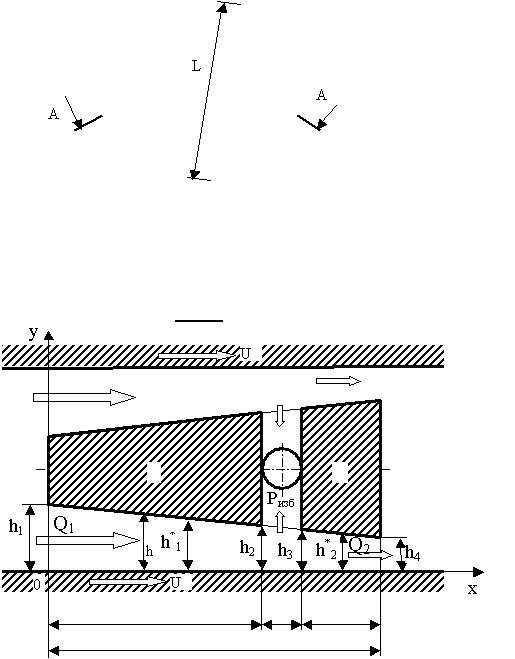
Рисунок 2 – Напорный сектор насоса.

Рассмотрим сечение А-А сектора по радиусу r. Из сечения видно, сектор можно представить как две упорные подушки I и II, расположенные друг за другом по ходу вращения дисков с отверстием между ними для отвода жидкости. Для каждой из подушек справедливо уравнение (1).

Для интегрирования  дифференциального уравнения (1) найдем связь между x и h. Нетрудно  видеть, что они связаны уравнением:

где  тангенс угла наклона поверхности опорной подушки к поверхности вращающегося диска. Из условия подобия трапеций (рис. 2) следует:

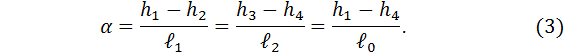
Продифференцировав уравнение (2), получим:

или

После подстановки dx в (1) получим:

Интегрируя полученное дифференциальное уравнение, получим для подушек I и II:

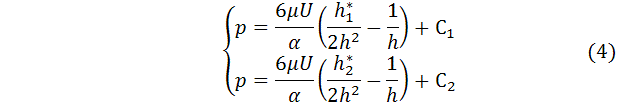
В этих уравнениях четыре неизвестных – постоянные интегрирования  и толщины гидравлического слоя  в сечениях, где dp/dx=0. Для их нахождения воспользуемся граничными условиями по давлению p на входе и выходе из подушек. На входе в подушку I и выходе из подушки II избыточное давление в жидкости равно 0. На выходе из подушки I и входе в подушку II (давление в прорези) оно равно pизб:

Подставляя граничные условия (5) в уравнение (4) получим систему из четырех уравнений с четырьмя неизвестными  и :

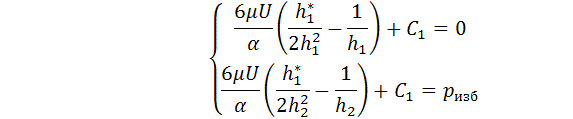
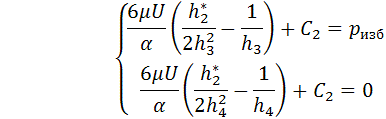
Решая эту систему уравнений  с учетом (3) относительно  и  получим:

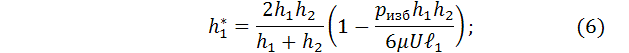
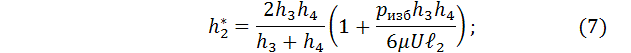
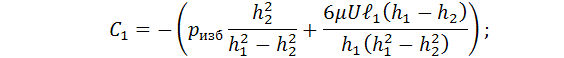
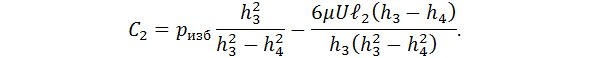
  После подстановки найденных констант в уравнения (4) и преобразований получим функцию распределения давления по длине подушек I и II:

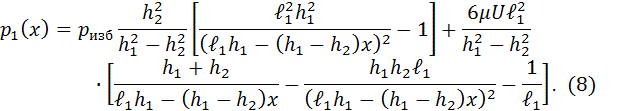
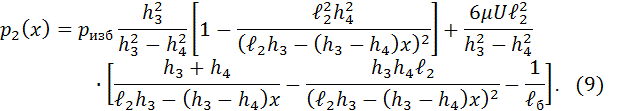
Разделим числитель и знаменатель выражения (8) на  и введя обозначение

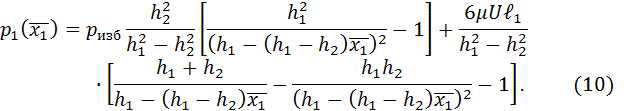
Разделим числитель и знаменатель выражения (9) на  и введя обозначение

 

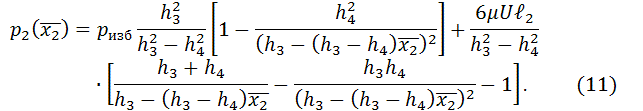
Учитывая, что скорость диска на радиусе r равна , длина подушки I на радиусе r равна длина подушки II на радиусе r равна , то уравнения распределения давления жидкости под секторами напорных подушек примут вид:

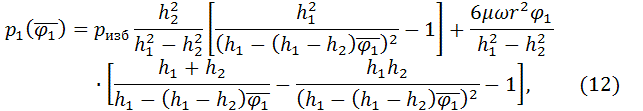
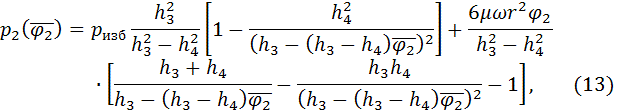
где:   

 

Подача жидкости через зазор между подушками.

Подача жидкости через прорезь между подушками I и II равна разнице между расходами жидкости через подушку I и подушку II:

Элементарный расход жидкости через поперечное сечение клинового зазора шириной dz, согласно теории, равен:

Используя уравнение (15) для элементарной трубки тока и заменяя dz на dr получим для подушки I и подушки II:

После подстановки  из выражений (6) и (7) после преобразований получим:


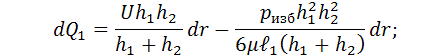
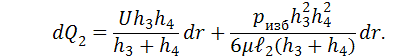
Учитывая, что  и  то уравнения элементарных расходов принимают вид:

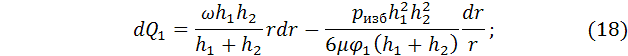
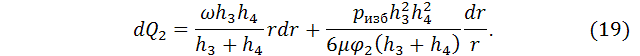
Интегрируя уравнения (18) и (19) от R1 до R2, получим:

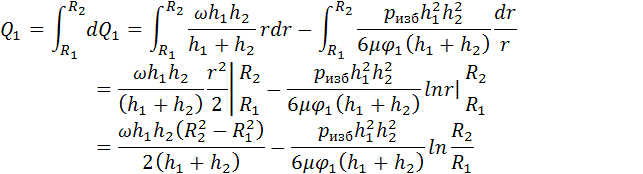
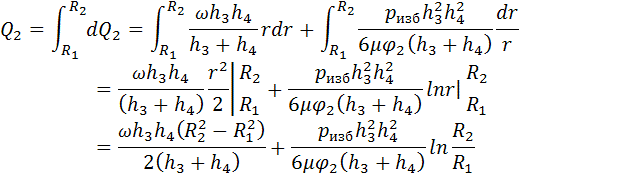
Расход жидкости через продольную щель составит:

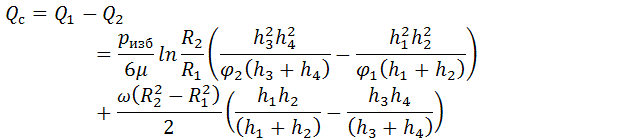
Одна напорная подушка имеет два клиновых зазора, вследствие чего подача одной напорной подушки в два раза выше подачи через клин, т.е.

 

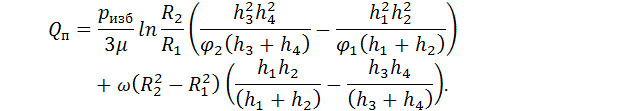
2.     Анализ полученных результатов.

Для анализа полученных теоретических зависимостей была рассмотрена секционная подушка, представленная на рис. 3, со следующими размерами, приведенными в табл. 1.

Таблица 1. Исходные данные для расчета.

ω

φ0

φ1

��щ

R0

R1

R2

L

h1

h4

об/мин

-

-

м

м

м

м

м

мм

мм

150

π/4

π/6

0.01

0.25

0.3

0.2

0.1

0.2

0.1

 

В качестве рабочей жидкости выбрано масло марки ТП-20 при температуре 40 оС. Результаты расчетов представлены на рисунках 3 и 4. В качестве оси абсцисс на рисунке 3 выбрана относительная координата , где L0 – длина подушки на радиусе R0 (см. рис. 2).

Из рисунка 3 видно, что распределение давления по длине подушки имеет форму двух пиков. При повышении избыточного давления в щелевом зазоре общий уровень давления в гидравлическом клине повышается, а пики давлений под подушкой I и подушкой II сближаются. Когда избыточное давление отбора жидкости из щели достигает некоторого максимального значения, в данном случае 552 кПа,  оба пика давлений сливаются, образуя единый пик.  В этом случае подушка начинает вести себя как целостная упорная подушка без поперечной щели. При этом отбор жидкости из гидравлического клина равен 0.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

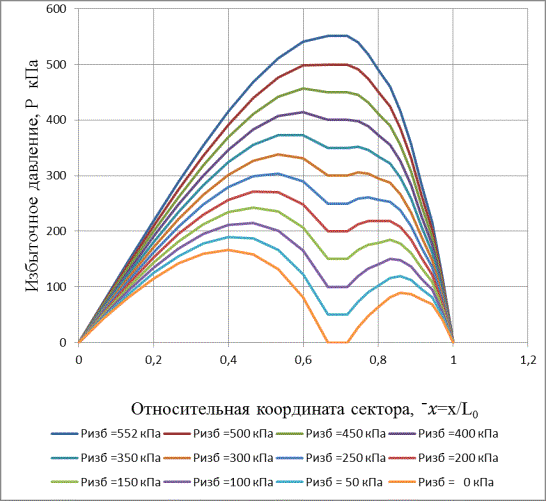
Рисунок 3 – Распределение избыточного давления в гидравлическом клине.

 

 

 

 

 

 

 

 

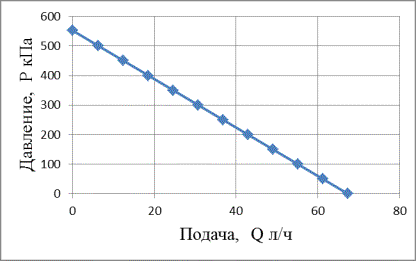
Рисунок 4 – Напорная характеристика гидропленочной подушки.

 

На рис. 4 представлена зависимость подачи жидкости через щель от избыточного давления в щели. По существу эта зависимость представляет собой напорную характеристику подушки как насоса. Из графика видно, что данная напорная характеристика носит линейный характер.

Выводы.

1. Проведенный математический анализ показал возможность создания насосов на базе течения жидкости в тонком гидравлическом клине.

2. Напорная характеристика такого насоса носит линейный характер, что позволяет прогнозировано изменять подачу насоса в широком диапазоне изменения давления.

3. Вращающиеся диски за счет двухстороннего давления жидкости при движении последней в клиновом зазоре находятся во взвешенном состоянии, вследствие чего исключается сухое трение их об напорные подушки неподвижных дисков.

4. При постоянной скорости вращения вращающихся дисков поток жидкости ламинарный и непрерывный, вследствие чего подача такого насоса носит плавный беспульсационный характер.

 

Литература.

1.      Чернавский C. А.. Подшипники скольжения. М., «МАШГИЗ», 1963.  243 с.

2.    Пуш В.Э. Металлорежущие станки. М.: Машиностроение, 1986. 564 с.