Б.И. Руднев, О.В. Повалихина

АНАЛИЗ ВЗАИМОДЕЙСТВИЯ РАДИАЦИОННЫХ ТЕПЛОВЫХ ПОТОКОВ

В КАМЕРЕ СГОРАНИЯ ДИЗЕЛЯ

Представлена теоретическая оценка взаимодействия потоков излучения и проанализированы основные особенности системы интегральных уравнений радиационного теплообмена применительно к камере сгорания дизельного двигателя

Ключевые слова: дизельный двигатель, камера сгорания, потоки излучения

B.I. Rudnev, O.V. Povalikhina

The analysis of interaction of radiative heat fluxes in diesel engine combustion chamber

Theoretical estimation of fluxes interaction radiation is given in this article. Main peculiarities of system of integral acquisitions of radiation heat transfer concerning diesel engine combustion chamber

Key words: diesel engine, combustion chamber, fluxes of radiation heat transfer

Излучающую систему для условий камеры сгорания (КС) дизельного двигателя можно представить как состоящую из четырех зон: трех поверхностных – поверхности крышки цилиндра F₁, втулки F₂ и поршня F₃, а также одной объемной зоны V, заполненной сажегазовой средой. Следуя [1] общую картину взаимодействия потоков излучения в произвольной точке М_k граничной поверхности F можно представить схемой, показанной на рисунке.

Рассмотрим более подробно воздействие основных потоков излучения для точки М_k, принадлежащей граничной поверхности F. В каждую точку граничной поверхности F приходит собственное излучение от объемной зоны M_i(V), т.е. Е_соб(М_i). Причем для всех точек граничной поверхности М_k, М_n, М_р иэтот поток является падающим потоком. В то же время каждая из поверхностей, на которых расположены точки М_k, М_n, М_р и, имеет свой эффективный (или исходящий [2]) поток излучения:

(1)

в свою очередь, отраженный поток для точки М_n может быть представлен следующим образом:

(2)

где – коэффициент отражения граничной поверхности F.

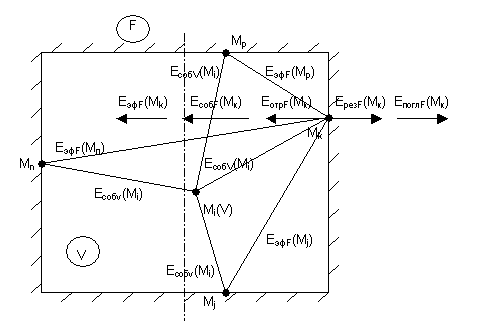
Рисунок. Схема взаимодействия потоков излучения в произвольной точке М_k граничной поверхности F

Figure. Scheme of fluxes interaction radiation in diesel engine combustion chamber at random point M_k adjacent surface F

Учитывая взаимосвязь между коэффициентом отражения и степенью черноты поверхности , имеем

(3)

Тогда эффективный поток излучения от точки М_п граничной поверхности F можно представить следующим образом:

(4)

Аналогично для точек М_р и:

(5)

(6)

Таким образом, для произвольной точки М_k граничной поверхности F (см. рис.) падающими потоками излучения будут Е_собV(M_i), Е_эфF(M_п), Е_эфF(M_p) и Е_эфF.

Результирующий поток излучения для точки М_k в общем виде запишется так:

(7)

Очевидно, что (7) эффективный поток излучения от точки М_k можно представить аналогично эффективным потокам от точек М_n, М_р и (4 – 6):

(8)

Подставляя в (7) соответствующие потоки излучения, определяемые по зависимостям (3 – 5, 7), получим

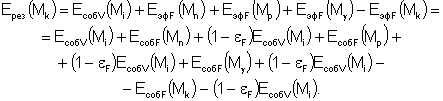(9)

Группируя в (9) члены, содержащие собственный поток излучения объемной зоны Е_собV(М_i), имеем

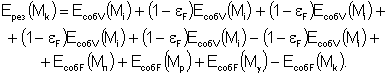(10)

Проанализируем полученную зависимость (10) для результирующего потока излучения произвольной точки М_k граничной поверхности F, выражающую функциональную связь основных потоков излучения. Из (10) следует, что результирующий поток излучения для точки М_k формируется при взаимодействии собственного потока излучения объемной зоны Е_собV(М_i) и собственных потоков излучения поверхностей, образующих граничную поверхность F: , , и . Причем собственный поток излучения поверхности, которой принадлежит точка М_k, имеет противоположный знак по отношению к собственным потокам излучения других поверхностей. Члены уравнения (10) вида представляют собой отраженный поток излучения от соответствующих элементов граничной поверхности F. Заметим, что при построении математической модели локального радиационного теплообмена в КС дизеля необходимо величину степени черноты граничной поверхности задавать дифференцированно по отношению к каждому ее элементу, т.е. отдельно для крышки цилиндра, поршня и втулки.

На основании экспериментальных данных [3] величины степени черноты для отдельных поверхностей, составляющих КС, имеют следующие значения: для днища поршня из алюминиевого сплава, покрытого нагаром толщиной 0,1 – 0,2мм, =0,91 – 0,95, а при толщине нагара 0,2 – 0,6мм, =0,94 – 0,97; для крышки цилиндра из чугуна, покрытой нагаром, =0,90 – 0,95; для втулки цилиндра с тонким слоем масла =0,3 – 0,4. Принимая во внимание величины степени черноты поверхностей КС, следует отметить, что члены вида в уравнении (10) важны в определенной мере лишь для поверхности втулки цилиндра. Для поверхности крышки цилиндра и поршня эти члены укладываются в погрешность определения температуры излучателя в КС дизеля и концентрации частиц сажи в ней. Напомним, что указанная погрешность составляет 15 – 20%. Однако даже и для втулки цилиндра величина не может быть значительной, так как в период активного процесса радиационного теплообмена в КС (от ВМТ до 80 – 100⁰ поворота коленчатого вала после ВМТ) большая часть втулки цилиндра перекрыта поршнем. Особенно это относится к дизелям с полуразделенными КС типа ЦНИДИ, ЯМЗ, КАМАЗ и др. Что же касается членов уравнения (10), представляющих собой собственные потоки излучения элементов граничной поверхности F: , , и ,– то здесь необходимо отметить следующее. Собственный поток излучения поверхности однозначно определяется ее температурой и излучательной способностью (степенью черноты) по зависимости

(11)

Аналогично можно определить и собственный поток излучения объемной зоны

(12)

В результате сложного взаимодействия рассмотренных выше потоков излучения между объемной зоной и соответствующими точками граничной поверхности в замкнутой системе (см. рис.) формируется результирующие потоки, определяющие радиационную тепловую нагрузку деталей КС. Этот процесс взаимодействия основных потоков излучения описывается системой неоднородных интегральных уравнений излучения (уравнения Фредгольма второго рода). Следуя [1, 3, 4] приведем указанную систему уравнений для условий в точке М_k

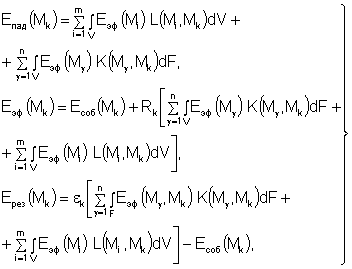(13)

где R_k, – коэффициенты отражения и поглощения (степени черноты) поверхности F в точке М_k; – произвольная точка поверхности F, лежащая вне окрестности точки М_k; М_i – произвольная точка объема V.

Интегральные операторы и называются ядрами уравнения, являются геометрическими функциями точек объема и поверхности и характеризуют систему как единый оптико-геометрический объект [1]. Проинтегрировав функции K и L по всей граничной поверхности, получим следующие уравнения связи геометрических и разрешающих локальных угловых коэффициентов излучения (ЛУКИ) [2]:

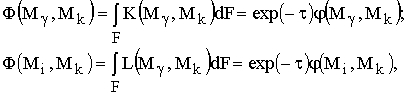(14)

где – число Бугера.

Следуя [1], под в (14) имеется в виду геометрический локальный угловой коэффициент излучения от элемента поверхности в окрестностях точки на элемент поверхности в окрестностях точки М_k, показывающий, какая доля эффективного излучения поверхности достигает поверхности с учетом многократных отражений на границе системы. Коэффициент имеет тот же смысл для излучения элемента объема в окрестностях точки М_i на поверхности . В свою очередь, и есть разрешающие коэффициенты, отличающиеся от соответствующих геометрических ЛУКИ тем, что они учитывают ослабление потока излучения вследствие поглощения и рассеяния энергии в объеме.

Приведенная система интегральных уравнений (13) вытекает из интегродифференциального уравнения переноса излучения, соответствующих граничных условий и соотношений, связывающих интенсивность излучения с различными характеристиками полусферического (поверхностного) и сферического (объемного) излучения [2]. По своей физической сущности интегральные уравнения (13) являются уравнениями состояния излучающей системы, поскольку описывают ее состояние как на границах, так и в объеме среды [2].

Для построения математической модели локального радиационного теплообмена в КС дизеля воспользуемся итерационно-зональным методом, предложенным Ю.А. Суриновым [5], а также работами, в которых раскрыты и проанализированы основные особенности применения зональных методов к расчету радиационного теплообмена в различных энергетических установках [2, 6].

В зональных методах расчета теплообмена излучением для систем, образованных излучающей, поглощающей и рассеивающей средами, ограниченными излучающими и отражающими границами, исходя из предложения, что излучающая система может быть приближенно заменена эквивалентной, составленной из оптически однородных изотермических подсистем. При этом поверхность границы излучающей системы F подразделяется на n изотермических оптических однородных непрозрачных зон: , а объем V, заполненный ослабляющей и излучающей средами, - на m объемных изотермических оптических однородных зон с полупрозрачными границами: . В [1] показано, что итерационно-зональный метод обобщает все основные постановки задач о радиационном теплообмене, имеющих единственное решение и различающихся способом задания граничных условий и характеристик поля излучения. Математическую основу этого метода составляет конечная система линейных алгебраических уравнений, аппроксимирующих соответствующую систему интегральных уравнений излучения типа (13).

Как известно [1, 5], для реальных излучающих систем R≠ 1; ≠ 1 и все интегральные уравнения излучения (13) имеют единственное решение. Для его получения воспользуемся итерационно-зональным методом алгебраической аппроксимации [5]. Сущность этого метода заключается в разделении реальной излучающей системы на конечное число объемных и граничных зон, в пределах которых оптические, энергетические и температурные характеристики могут быть осреднены или заданы аналитически [1, 5]. В этом случае исходное интегральное уравнение излучения может быть заменено соответствующей системой линейных алгебраических уравнений, число которых равно числу зон в системе. Алгебраическая аппроксимация интегрального оператора возможна как в исходном интегральном уравнении, так и в уравнении резольвенты. В связи с этим точное решение исходного интегрального уравнения может быть выражено через резольвенту интегрального оператора или непосредственно через разрешающие угловые коэффициенты излучения. В соответствии с этим алгебраическая интерпретация решения может быть представлена в общем виде или через резольвенту [1, 5]. Алгебраическая аппроксимация точного решения исходных интегральных уравнений излучения (13) согласно [1] будет иметь вид

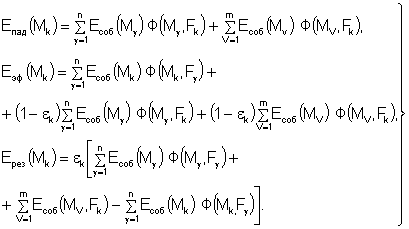(15)

Уравнения (15) получены в предложении, что излучающая система состоит из n граничных и m объемных зон, а в качестве первой итерации принято условие равенства эффективных потоков излучения в пределах зоны соответствующим потокам собственного излучения этих зон.

Путем замены в интегральном операторе переменного ЛУКИ постоянным, осредненным в пределах рассматриваемой зоны, можно систему интегральных уравнений резольвент поверхностного и объемного излучений привести к соответствующим системам алгебраических уравнений. Принимая, что в пределах каждой граничной зоны приближенно выполняется условие , в [1, 5] получены следующие системы аппроксимирующих уравнений резольвент поверхностного излучения:

(16)

и объемного излучения

(17)

где – средний угловой коэффициент излучения зоны на зону k, определяемый по зависимости

В результате этих действий система интегральных уравнений излучения (13) приводится к эквивалентной конечной системе линейных алгебраических уравнений. Решение последней позволяет определить мгновенное локальное распределение по элементам граничной поверхности всех видов потоков излучения.

Проведенный анализ системы интегральных уравнений и теоретические оценки взаимодействия потоков излучения позволили сделать ряд существенных уточнений в зональной модели радиационного теплообмена в КС дизельного двигателя [7] и других энергетических установок [8].

Список литературы

1. Петриченко, Р.М., Элементы автоматизированного проектирования ДВС: Алгоритмы прикладных программ [Текст] / Р.М. Петриченко, С.А. Батурин, Ю.Н. Исаков [и др.] – Л.: Машиностроение, 1990. – 328 с.

2. Блох, А.Г. Теплообмен излучением: Справочник [Текст] / А.Г. Блох, Ю.А. Журавлев, Л.Н. Рыжков. – М.: Энергоатомиздат, 1991. – 432 с.

3. Modest, M.F. Radiative Heat Transfer. [Тext] / M.F. Modest. – New York: Academic Press, 2003. – 822 p.

4. Dombrovsky, L.A. Radiation Heat Transfer in Disperse Systems [Тext] / L.A. Dombrovsky. – New York: Begell House, 1996. – 256 p.

5. Суринов, Ю.А. Об итерационно-зональном методе исследования и расчета лучистого теплообмена в поглощающей и рассеивающей среде / Ю.А. Суринов. // Известия СО АН СССР. 1978. – №8. – Вып. 2. – С. 106 – 125.

6. Суринов, Ю.А. Современное состояние и перспективы развития теории переноса излучения и радиационного теплообмена / Ю.А. Суринов // Труды первой Российской национальной конференции по теплообмену. В 9т. Т. 9. Радиационный и сложный теплообмен. – М.: Изд-во МЭИ, 1994. – С. 238 – 243.

7. Руднев, Б.И. Анализ использования зональной модели радиационного теплообмена в камере сгорания дизельного двигателя / Б.И. Руднев, О.В. Повалихина // Труды пятой Российской национальной конференции по теплообмену. В 8 т. Т. 6. Интенсификация теплообмена. Радиационный и сложный теплообмен. – М.: Издательский дом МЭИ, 2010. – С. 261 – 263.

8. Кулешов, О.Ю. Повышение вычислительной эффективности зонального метода расчета сложного теплообмена на основе методики коррекции базовых оптико-геометрических характеристик излучения / О.Ю. Кулешов, В.М. Седелкин // Труды пятой Российской национальной конференции по теплообмену. В 8 т. Т. 6. Интенсификация теплообмена. Радиационный и сложный теплообмен. – М.: Издательский дом МЭИ, 2010. – С. 227 – 230.