К.т.н. Павлюков В.С., инж. Павлюков С.В.

«Южно-Уральский государственный университет»(НИУ)

РАЗВИТИЕ НА БАЗЕ ЭЛЕМЕНТОВ ИСКУССТВЕННОГО ИНТЕЛЛЕКТА МОДЕЛИРОВАНИЯ УЧЕТА ПИТАЮЩЕЙ СЕТИ К ЗАДАЧЕ КОМПЛЕКСНОЙ ОПТИМИЗАЦИИ

ЭКСПЛУАТАЦИОННЫХ СХЕМ РАСПРЕДЕЛИТЕЛЬНЫХ ЭЛЕКТРИЧЕСКИХ СЕТЕЙ ПО ПОТЕРЯМ ЭЛЕКТРОЭНЕРГИИ

Аннотация Рассмотрен новый подход к моделированию совместной работы питающей и распределительной сетей применительно к задаче минимизации потерь электроэнергии в обеих сетях. Поскольку в сетях на интервале времени Т (суточном) происходит изменение режимной ситуации, в частности узловой нагрузки, то требуется ее прогнозирование, выполненное с использованием элементов искусственного интеллекта.

Ключевые слова: графики нагрузки, потери электроэнергии, градиент потерь, нейронная сеть, алгоритм обучения нейронной сети.

I. Введение Для электроэнергетики России одной из важных задач является задача снижения технологических потерь электрической энергии, связанных с новыми условиями организации ее транспорта и распределения. Согласно данным Росстата в 2008 г. потери электроэнергии составили 11,43% от общего количества энергоресурсов. Поэтому задача уменьшения потерь энергии заслуживает серьезного внимания. Наиболее эффективным и относительно малозатратным мероприятием по снижению потерь в распределительных электрических сетях является поиск и реализация оптимальных мест размыкания контуров схемы. Поиск мест размыкания путем решения задачи оптимизации эксплуатационной схемы распределительной электрической сети по потерям электроэнергии без учета питающей сети приводит к снижению потерь электроэнергии только в распределительной сети. При этом потери электроэнергии в питающей сети становятся неконтролируемыми и могут даже возрасти. Предлагается питающую и распределительную сети рассматривать при совместной работе в едином электротехническом комплексе. Такой подход связан с дальнейшим совершенствованием указанной задачи и направлен на повышение эффективности работы объединенных сетей энергосистемы.

II. Постановка задачи и методика решения Задача минимизации потерь мощности рассматривалась многими авторами, но обособленно в питающих и распределительных сетях[1]. Такой же подход используется и в современных трудах [2-3]. Известными методами при существующей разнородности графиков нагрузок в узлах сетей не обеспечивается получение оптимальных решений. Поэтому, в отличие от известных методов, предлагается не имеющая аналогов модель объединенной работы сетей, позволяющая в условиях разнородности графиков нагрузок в узлах сетей обеспечить наибольшее снижение потерь электроэнергии. Данную задачу решают не только для расчетов, связанных с текущей эксплуатацией сетей, но и предсказаний на перспективу с использованием элементов искусственного интеллекта.

Модель градиента потерь электроэнергии, предложенная в [4], базируется на рассмотрении питающей сети как управляемой системы в пространстве независимых управляющих параметров, посредством которых моделируются положения мест размыканий контуров схемы распределительной сети [5], требует трудоемких процедур формирования подблоков расчетной матрицы коэффициентов узловых сопротивлений на основе матрицы формулы потерь В и множителей Эта модель имеет большой объем вычислений и ухудшает быстродействие алгоритма совместных расчетов сетей. Множители скалярных произведений графиков нагрузок узлов и питающей сети определяются формулой , коэффициенты – скалярными произведениями графиков нагрузок узлов распределительной сети и узлов питающей сети, множители – скалярными произведениями графиков модулей токов узлов и , через которые в контурах схемы распределительной сети возможны перемещения точек размыкания на соседние участки.

Для данной задачи графики нагрузок узлов представим в виде среднего за период Т и центрированной функции

. (1)

Тогда множители 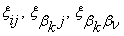будут определяться следующими выражениями:

(2)

(3)

(4)

где ; (5) ; (6) . (7)

Функция потерь электроэнергии принимая во внимание (2-4), в алгебраической форме запишется в виде

(8)

Составляющая в выражении (8) характеризует потери электроэнергии, определяемые из расчета установившегося режима питающей сети для указанной задачи оптимизации при задании исходных режимных параметров в виде узловых нагрузок, равных их средним значениям .

Входящая в формулу (8) составляющая представляет среднее функции потерь электроэнергии на отрезке времени [0,Т]. Элемент обозначает матрицу расчетных контурных сопротивлений питающей сети. Параметр рассматривается как независимая непрерывная переменная[5]. Произведения 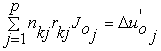в вычисляют среднее значение разностей модулей напряжений между узлами связи питающей и распределительной сетей (p-количество узлов связи сетей). Принадлежность узлов связи сетей j питающей сети отдельным контурам схемы распределительной сети определяется второй матрицей соединений .

Составляющая потерь электроэнергии (8), представляет функцию, зависимую от скалярных произведений соответствующих центрированных функций графиков нагрузок узлов сетей.Элементы матрицы контурных сопротивлений корректируются множителями (7).

Градиент функции потерь электроэнергии (8) с учетом выше изложенного представится суммой двух компонент

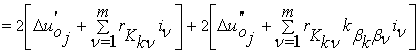, (9)

где , – составляющие, первая из которых соответствует среднему значению функции потерь, вторая–корректирована множителями (7).

Матричное уравнение для выражения (9) в краткой форме запишется как

, (10)

где – матрица расчетных контурных сопротивлений схемы питающей сети, эквивалентных по потерям электроэнергии на рассматриваемом отрезке времени [0,T]. Следует отметить, что в выражении (10) первая составляющая является доминирующей, что подтверждается экспериментальными данными. Если воспользоваться упрощенным характером модели режима сети, то узловые нагрузки на интервале времени [0,Т] можно представить областью средних значений (1). Оценки среднего определяются с помощью эксплуатационных записей нагрузок в диспетчерских ведомостях, содержащих графики нагрузок узлов за период времени Т. Использование упрощенной модели режима не вносит большой погрешности в определение параметров режима [6] и функции потерь электроэнергии для объединенных сетей, но позволяет существенно уменьшить объем и сложность алгоритма вычисления (10). Для составляющей градиента можно применить процедуру определения ее непосредственно на основе расчета установившегося режима, что исключает при этом формирование большого объема .

Модель учета питающей сети при совместной работе сетей будет состоять в следующем. По аналогии с моделью графика (1), вектор узловых нагрузок будет иметь вид

, (11)

где – вектор средних значений нагрузок в узлах сети за период времени Т; –вектор центрированных узловых нагрузок за тот же период времени.

На основе выражения (11), составляющие вектора напряжений в узлах питающей сети запишутся в подобном виде:

; (12)

, (13)

в которых и определяются расчетом потокораспределения в сети при моделировании в ее узлах нагрузок средними значениями.

Учитывая, что в данном подходе вектор нагрузок определяется выражением (11), целевая функция потерь электроэнергии и ее градиент будут иметь аналогичный вид. Определим компоненту градиента потерь . Модель функции среднечасовых потерь электроэнергии , обусловленная нагрузками , выразится следующей формулой

, (14)

где G – матрица активных узловых проводимостей питающей сети; T – операция транспонирования.

При оптимизации схемы распределительной сети, как указывалось в [5], используется градиентный метод. В связи с этим на каждом шаге итерационного процесса необходимо вычислять компоненты градиента в виде частных производных от функции (14). Для определения частных производных существует достаточно методов [8], но они требуют многократного решения уравнений установившихся режимов. Чтобы избежать этой неэффективной процедуры, предлагается подход, который сводится к однократному решению системы линейных алгебраических уравнений, полученной с помощью узловых уравнений. Принимая во внимание зависимость потерь электроэнергии от нагрузок в узлах, которые в свою очередь являются функциями от параметров , составляющая определится в соответствии с выражением

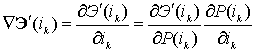. (15)

Используя записи функций узловых активных мощностей сети и токов , определим 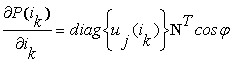в формуле (15). Составляющую 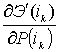найдем из матричного уравнения

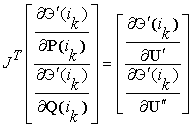. (16)

Здесь J – матрица Якоби, а правая часть системы (16) получена с использованием операции дифференцирования формулы (14).

Заметим, что матрицу коэффициентов Якоби J системы уравнений (16)

можно получить после расчета уравнений баланса узловых мощностей в прямоугольной системе координат(можно использовать и другие системы координат). Частные производные 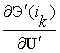и 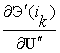правой

части системы (16) можно определить аналитически, решая систему матричных уравнений, полученную дифференцированием выражения (14):

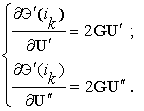(17)

В итоге реализован подход определения составляющая вектора-градиента .

Представленная модель имеет меньший объем вычислений по сравнения с [9] и повышает быстродействие алгоритма модели совместной работы сетей в 2…3 раза. Оптимизацией схемы распределительной сети при обособленной работе обеспечивает снижение потерь электроэнергии около 20% . При совместной работе питающей и распределительной сетей оптимизация приводит к снижению потерь в распределительных сетях до 16%. При этом потери в питающих сетях уменьшаются примерно на 4%.

Полученную модель учета питающей сети можно использовать как для анализа режимов в эксплуатационных условиях, так и для прогноза. Но в последнем действии необходимо решение задачи прогноза временных рядов, то есть графиков производства, потребления электроэнергии. К решению этой задачи можно привлекать такие разделы математики как сплайн-функции, теорию Эйлера-Фурье, факторные модели, вероятностные модели в виде стационарного Марковского процесса и др. Для решения указанной задачи наметилась тенденция применения элементов искусственного интеллекта, к которым относятся нейронные сети. Использование нейронных сетей в области задач управления различными системами оказалось перспективным направлением. Упомянутые выше методы для целей прогнозирования временных рядов громоздки, сложны для алгоритмизации и работают в основном на базе числовых данных.

Технические системы, в том числе электроэнергетическая, работают по определенному ритму, в котором внешнее и внутреннее ее состояние во многом повторяется через определенные промежутки времени. Используя наблюдения или измерения работы системы в момент времени t, можно предсказать ее работу в момент времени t+d, то есть ожидаемое в перспективе состояние. Подобные задачи позволяют решать Multiple layer perceptron–MLP(многослойные нейронные сети). Выбор или разработка нейронной сети зависит от типа задачи и ее сложности. В настоящее время существуют наработки по нейронным сетям[9], но они не являются универсальными. Под конкретную задачу разрабатывают необходимую архитектуру нейронной сети со всеми ее атрибутами. Нейронная сеть представляет собой математическую модель особой конструкции, под которой понимается ее определенная многослойная архитектура и способы ее обучения для решения задач. При обучении сети использовался алгоритм обратного распространения (Backpropagation algorithm)–это самый на сегодняшний день, изученный и эффективный способ для обучения нейронных сетей. Не раскрывая подробностей из-за малого объема статьи, приведем результаты работы сети.

III. Результаты Правильная реакция нейронной сети на входной сигнал(или на вектор входного сигнала) является (задано по условию задачи). Реальное значение выходного сигнала, рассчитанного сетью, равно 0,725. Среднеквадратичная ошибка составила 0,038.

Если результат не удовлетворяет поставленной задаче, то для уточнения или дальнейшего обучения нейронной сети применяют специальные приемы, например, упомянутый выше, алгоритм обратного распространения ошибок. Функции данного алгоритма будут представлять обратный ход текущей эпохи. После работы процедуры Backpropagation algorithm убеждаемся, что действительно ошибка на выходе сети уменьшается при вводе того же обучающего сигнала ещё раз:

Одна эпоха алгоритма обратного распространения позволила уменьшить среднюю ошибку на 0,004. На сотой итерации ошибка составляла , на тысячной –, на десятитысячной – , на стотысячной –.

Тестирующий вектор входных данных показал адекватность модели нейронной сети получением максимально близкого желаемого результата: начальная ошибка была равна 0,025. Текущая ошибка составляет 0,023, то есть, средняя ошибка уменьшилась на 0,002. Результат обучения оказался успешным.

Также были исследованы результаты работы сети с другими активационными функциями в режиме обучения. Результаты получены следующие: для функции : на первой итерации ошибка составляла 0,037, на второй – 0,034, на сотой – , на тысячной –, на десятитысячной–, на стотысячной–; для функции : на первой итерации ошибка составляла 0,038, на второй – 0,034, на сотой – , на тысячной –, на десятитысячной – , на стотысячной – ; для функции на первой итерации ошибка составляла 0,034, на второй – 0,033, на сотой – , на тысячной –, на десятитысячной – , на стотысячной – ; для функции: на первой итерации ошибка составляла 0,036, на второй – 0,035, на сотой – , на тысячной –, на десятитысячной – , на стотысячной – . Результаты расчетов оказались достаточно близки с тестовыми.

Пример, проиллюстрированный выше, далее развит для прогноза временных функций, которые моделируют графики нагрузок узлов для разных интервалов времени Т. Например, внутри суток наблюдаются повторяющиеся физические изменения, связанные с технологическими и социальными процессами, поэтому они классифицируются по типу дня. Для исследований, по мере надобности, суточный разрез времени характеризуется учетом некоторых метеорологических факторов.

Модель сети обучалась с использованием режимных данных за прошедшие с G по G-3 годы с сопутствующими метеорологическими условиями для конкретных узлов региональной электрической сети. Анализ погрешностей результатов 24-часового прогноза для рабочих суток по данным указанных лет, варьировался от 3,9 до 2,8% и, примерно, от 0,4% до 0,6% больше для нерабочих суток. Несколько меньше погрешность получалась(примерно на 0,3-0,5%) для отдельных периодов рабочих суток с более или менее равномерно распределенной нагрузкой. При прогнозировании среднесуточной нагрузки узлов, по данным указанного выше интервала времени, погрешность не превышала 1,63%.

IV. Выводы Данный способ расчета позволяет отказаться от формирования матрицы узловых сопротивлений, в которой нет нулевых элементов. Однако данный метод имеет преимущества перед ранее предложенным методом [9] в том случае, если моделирование режима питающей сети воспроизводится средним значением градиента функции потерь электроэнергии. Рассмотренный подход позволил относительные приросты потерь в (15) вычислить решением системы линеаризованных уравнений с матрицей коэффициентов Якоби(16), что улучшило вычислительные характеристики алгоритмов учета. Предложенный метод свободен от трудоемких вычислений, более прост в алгоритмизации расчетов и может быть использован при решении подобной задачи в других областях.

Рассмотренная модель нагрузок (1) без учета центрированной составляющей, позволяет существенно сократить время решения задачи, получить в условиях разнородности графиков нагрузок узлов, используя выше приведенные скалярные множители , решения, оптимальные по потерям электроэнергии, что в настоящее время становится актуальным в условиях взаимовыгодных расчетов между отдельными ПЭС в сфере преобразований рынка электроэнергетики.

Предложенные модели совместной работы сетей с применением элементов искусственного интеллекта являются перспективной технологией для данной задачи.

Литература:

1. Казанцев В.Н. Методы расчета и пути снижения потерь энергии в электрических сетях.– Свердловск: УПИ, 1985. – 84 с.

2. Воропай Н.И., Бат-Ундрал Б. Расчеты режимов радиальной электрической сети интервальным методом // Электричество. 2008. №10.

3. Бат-Ундрал Б. Минимизация потерь в распределительной электрической сети на основе выбора месте размыкания с использованием алгоритма колонии муравьев // Материалы Всероссийской научно-технической конференции «Повышение эффективности производства и использования энергии в условиях Сибири», Иркутск: ИрГТУ. 2010.

4. Фомин Н.И., Павлюков В.С. Метод определения потерь электроэнергии в питающей сети для задачи комплексной оптимизации схем распределительных электрических сетей // Электробезопасность. Челябинск. 1999. №3-4. С. 3-7.

5. Ушаков И.М., Павлюков В.С., Фомин Н.И. Оптимизация мест размыкания в распределительных электрических сетях по потерям электроэнергии//Пути экономии и повышения эффективности использования электроэнергии в системах электроснабжения промышленности и транспорта. Всесоюзная научная конференция: Тезисы докладов.– Казань, 1984. С. 163-164.

6. Паздерин А.В., Плесняев Е.А., Конов Г.А. Исследование математических моделей распределения потоков электрической энергии. Э65 Энергосистема: управление, качество, безопасность: Сборник докладов Всероссийской научно-технической конференции, Екатеринбург: УГТУ-УПИ. 2001. С. 461-464.

7. Самсонов Е.Ю. Расчет удельных приростов потерь по матрице узловых проводимостей сетей // Энергетика…(Изв. высш. учеб. заведений). 1986. № 3. С. 38-41.

8. Хайкин С. Нейронные сети: полный курс.–М.: ИД Вильямс. 2006. 1104 с. 1001

9. Методы учета питающей сети для задачи оптимизации эксплуатационных схем распределительных электрических сетей по потерям электроэнергии / Павлюков В.С., Фомин Н.И. –Челябинск: ЮУрГУ. 2000. 6 с.–Деп. в ВИНИТИ. № 2410-В00.