Ткаченко О.С.

Загальноосвітня школа І-ІІІ ступенів № 4 м. Красноармійська, Україна

Інтегральне обчислення в різних сферах суспільного життя.

Поняття інтеграла – важливе у шкільному курсі математики, в курсі вищої математики,що розгалужується на низку цікавих, хоч і складних, математичних дисциплін: математичний аналіз, функціональний аналіз, теорія функції комплексної змінної, диференціальні рівняння, теорія ймовірностей, теорія оптимізації математичних процесів

Окрім математичних, є науки, що широко використовують математичний апарат і нині дуже популярні, оскільки необхідні для ведення різноманітних справ, для гармонійного розвитку галузей виробництва, тощо. У цих науках також використовується поняття інтеграла. Серед них такі як: економіка виробництва, фінансова справа, електроніка, програмування, фізика, хімія, радіофізика.

Кожна людина рано чи пізно задає собі питання: яке значення в їх житті відіграє математика? Відповідь на це питання приходить не одразу,а через деякий час. Виявилося,що без таких складний речей,як інтегральне числення,наше повсякденне життя будо б досить важким.

На прикладі задач ми спробуємо показати,як за допомогою інтегрального обчислення знаходити розв’язки задач з економіки, фізики, фінансах і т.д.

Задача

Знайти довжину шини машини, радіус якої дорівнює R.

Розв’язання:
Знайдемо ¼ частини довжини шини від точки (0; R) до точки (R; 0). Так як y = , тоді L = dx = R arcsin = 2π R.

Відповідь: L = 2πR

Завдяки знанням про інтеграли можна обчислити довжину лінії серця людини,якщо не брати до уваги,що воно у кожній частині має різні розміри. Давайте на це поглянемо на прикладі:

Задача

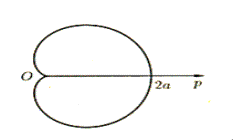Знайти довжину лінії серця,якщо r = a (1 +cos  ).

Розв’язання:

Лінія ,r = a (1 + cos  ) ,симетрична щодо полярної осі. Знайдемо половину
довжини серця:

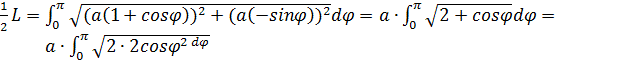= 2a

Відповідь: 4a.

Задача

Визначити величину вкладу через 2 роки, якщо початковий капітал 50 000 грош. од., процентна ставка 8%.

Розв’язання:

Використовуючи формулу , отримаємо загальну величину вкладу через 2 роки:

S =

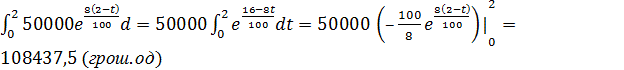
Відповідь:108437,5 грош.од.

Робота археолога-не тільки,як здавалося б,копати,збирати та очищувати артефакти і скарби. Праця археолога займає набагато ширшу ланку,ніж ми собі уявляємо, адже вони мають обчислювати площі та об’єми ділянки,на якій ведуться розкопки,а без використання інтегралів це зробити майже неможливо.

Задача

Нещодавно археологи при розкопуванні стародавніх поселень знайшли жертовне місце, яке їх дуже зацікавило. Після досліджень було з’ясовано, що це тіло, утворене обертанням параболи у = – х² + 2х + 3 навколо вісі Ох (х вчені вимірювали в метрах). Причому виготовлений він був з каменю густиною 2500 кг/м³. Яка масу каменя використали на виготовлення цього жертовника стародавні майстри?

Розв’язання.

Побудуємо фігуру, обмеженою параболою y=-x²+2x+3, вісями Оу та Ох.

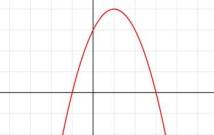
Об’єм тіла обчислюється за формулою: 

V =

V=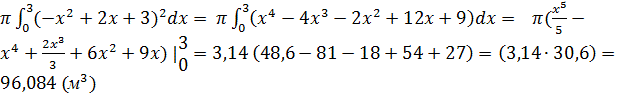

m=96,084

Відповідь. 240210 кг.

Для того,щоб зручніше будо обчислювати швидкість, силу, потужність, силу струму, густину і теплоємність фізики використовувати інтеграли-це набагато зручніше!

Задача

Знайти площу пелюстка ромашки, який розміщено  між дугами парабол

Розв’язання:

Дана фігура обмежена графіками двох функцій: y=x² та у=

Шукана площа за допомогою інтеграла обчислюється так:

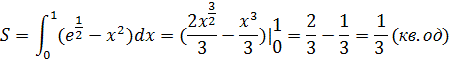
Відповідь. 1/3 кв. од.

Задача

Навантаження  на Курахівську теплоелектростанцію задається функцією f(x) = 3x² + 4x – 2. Визначити витрати електроенергії протягом доби.

Розв’язання:

N(x) =

N(x)=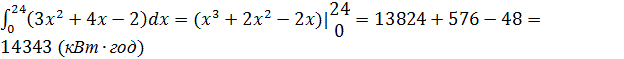

Відповідь: 14343 кВт·год.

Задача

Задана функція граничних витрат (витрати на виробництво додаткової одиниці продукції товару) C = 2 q² − 14 q + 250 . Знайти функцію витрат C = C ( q ) і обчислити витрати у випадку виробництва 15 одиниць товару.

Розв’язання:

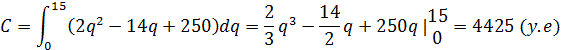
Знаходимо інтегруванням витрати на виготовлення 15 одиниць товару.

Відповідь: 4425 у.е.

Задача

Швидкість викиду крові з серця за деякий час описується деякою функцією v(t)=3t²-2t . Період серцевого скорочення t₀=1c, час систоли t₂=0,1с. Визначите хвилинний обсяг викидається крові V_хв.

Розв’язання:

V_хв=

V_хв = .

Обчислюємо за формулою Ньютона – Лейбниця і отримуємо:

V_хв =

Відповідь:

Висновок:

Важко назвати наукову область, у якій би не застосовувалися методи інтегрального вирахування, загалом, і властивості визначеного інтеграла.

Інтегральне обчислення може використовуватися в області фізики, геометрії, механіки, біології й економіки, медицини. Звичайно, це ще далеко не вичерпний список наук, які використають інтегральний метод для пошуку встановлюваної величини при розв’язанні конкретного завдання, і встановленні теоретичних фактів. В даній статті була зроблена спроба огляду основних відомостей про визначений інтеграл та його застосування в різних сферах суспільного життя.