Математика/2. Дифференциальные и интегральные уравнения

Рашевський М.О.

ДВНЗ «Криворізький національний університет», Україна

Про асимптотичне інтегрування лінійних систем з двома малими параметрами

Питання про асимптотичні розв’язки лінійних систем вигляду

, (1)

досліджувалось у роботах [2, 3], де побудовані згадані розв'язки. Тут x(t, e, m) – невідомий вектор; h + p ³ 1; n ´ n – матриці A(t, e, m) та D(t, e, m) мають на скінченному проміжку [0, L] рівномірні асимптотичні розвинення вигляду 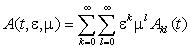за степенями дійсних малих параметрів e > 0, m > 0. Вимагалося виконання умови

1⁰. Матриці A_kl (t) та D_kl (t) є нескінченно диференційовними на проміжку [0; L].

Припускатимемо надалі, що виконуються такі умови.

2⁰. D(t, e, m) º E, де E – одинична матриця.

Можна також вимагати виконання менш жорсткої умови det D(t, e, m) ¹ 0, тобто відсутності виродження, яке у цій роботі не вивчається.

3⁰. Корені характеристичного рівняння є різними на (0, L], і збігаються при t = 0 так, що матриця A₀₀(0) подібна жордановій клітці розміру n.

Наступною підстановкою

(2)

із (1) дістанемо систему

, (3)

де .

Зображення матриці системи (3) запишемо як .

Доведення наступної теореми принципово не відрізняється від доведення теореми 2. 5-1 із [4].

Теорема 1. Якщо виконуються умови 1⁰, 2⁰, то система (1) невиродженим перетворенням (2) зводиться до (3) із арнольдовою формою A⁽¹⁾(t, e, m) матриці A(t, e, m), що має нульову діагональ.

Згідно зі структурою арнольдової форми матимемо:

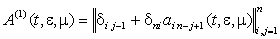, тобто крім одиниць жорданової клітини ненульовими є лише елементи останнього рядка матриці, який записується як

; .

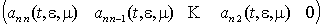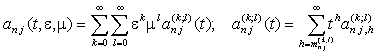Таким чином, – кратність нуля функції , у точці t = 0, яка є внаслідок умови 3⁰ точкою повороту (ТП) [1] – [4].

У загальному випадку асимптотичні розв’язки системи (3) будують багатомасштабним методом [3, 4], який розробляється для випадку двох параметрів, щоб враховувати співвідношення між ними. Тут використаємо метод [1] для побудови асимптотичного розв'язку згаданої системи із простою ТП у припущенні, що , тобто ТП є простою. Для малих параметрів виконується одне із співвідношень

А) me ^– 1 « 1, або Б) em ^– 1 « 1.

Нехай виконується умова Б), а також h = p = 1. Для використання методу [1] вимагатимемо виконання умови

4⁰. .

Згідно з [1] корені характеристичного рівняння є простими на досліджуваному проміжку. Тому існує невироджена матриця T(t, e, m) така, що , де – діагональна матриця, елементи якої є внаслідок 4⁰ такими, що .

Записавши матрицю системи у вигляді так, що A_k(t, e, m) є обмеженими при прямуванні до нуля параметрів m і e, будуватимемо формальний розв’язок системи (3) у вигляді

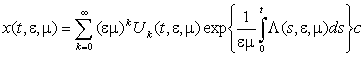;. (4)

Для визначення невідомих матриць прирівняємо коефіцієнти при степенях me у тотожності .

З урахуванням групування доданків матимемо систему рівнянь

,

де .

Розв’язність останньої системи встановлюється методом [1]. Побудувавши невідомі матриці, переконуємось у справедливості наступного твердження.

Теорема 2. Якщо виконуються умови 1⁰ – 4⁰,то система рівнянь (3) на проміжку [0, L] має формальний розв’язок (4).

Характер особливостей побудованих матриць з’ясовує така лема.

Лема. Якщо виконуються умови 1⁰ – 4⁰, а також умова Б) і , то для норм матриць U_k(t, e, m) справджуються оцінки , де С – стала, що не залежить від e і m.

З урахуванням леми сформулюємо твердження про асимптотичний характер розв'язку (4). Враховуючи взаємну залежність параметрів, побудуємо m₁, m₂ – наближення [1, 2], яке запишеться як , тобто є m – наближенням по параметру e×m.

Теорема 3. Нехай виконуються умови теореми 2 і леми. Тоді для m – наближення , отриманого із (4) і деякого точного розв'язку x(t, e, m) системи (3) таких, що на проміжку [0, L] справджується нерівність ,

Тут 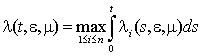, а С – стала, що не залежить від e і m.

Детальніше вище записана оцінка записується у вигляді Оцінка норми в останній нерівності показує, що при виконанні умови Б) разом з e і m, але не для довільних m₁ і m₂, тобто не для довільного m.

Враховуючи умову Б), можна стверджувати, що існує додатне число r < 1 таке, що m = e^r. Тоді остання нерівність запишеться як

.

Остання нерівність доводить існування m такого, що незалежно від r справджується оцінка .

Зауваження. Обмеження h = p = 1 не принципове. Для довільних h і p розвинення необхідно вести за степенями e^hm^p, попередньо записавши аналогічне розвинення для матриці системи.

Література:

1. Шкиль Н.И. О периодических решениях систем дифференциальных уравнений второго порядка // Arch. Math. (Brno). - 1987. – 23, № 1.– P. 53-62.

2. Яковец В.П. Асимптотика общего решения линейной сингулярно возмущенной системы с двумя малими параметрами. //ДУ. 1993. Т. 29, № 2. С. 256-266.

3. Iwano M., Sibuya Y. Reduction of the order of a linear ordinary differential equation containing a small parameter // Kōdai Math. Semin. Repts.- 1962. - 36, №3.- p. 1-28.

4. Wasow W. Linear Turning Point Theory. – N.Y.: Acad. Press, 1985. – 246 p.