Применение виртуализации для механизмов высоких классов Л.В. Ассура.

К.ф.-м.н. Джанузаков С.Д.

Магистрант МУИТ Иманбаев А.К.

Магистрант МУИТ Есмухамедов Н.С.

Способ абстрагирования, путем которого объекты реального мира, обладающие множеством параметров и характеристик, подменяются образами воображаемых, иначе говоря, искусственных объектов, называется виртуализация. В отличие от реальных объектов, такие образы, как искусственные, называются виртуальными объектами. Необходимо отметить, что в большинстве случаев, использование искусственных образов, которые имеют наименьшие характеризующие параметры, во многом облегчают исследовательскую работу над определенной проблемой.

Для явного и открытого примера, можно взять обычные процедуры в быту которые сопровождают нас постоянно или же время от времени. Раньше пользователям коммунальных/банковских/других услуг приходилось часами стоять в очередях в целях оплаты за услуги представителю. Сейчас же разного рода оплаты и переводы можно проводить в виртуальном мире которая сопровождает нас постоянно. Люди пользуются виртуализацией валюты и не подозревают об этом. Понятие виртуализации имеет широкое использование в информационных технологиях, в частности в компьютерных технологиях. При выполнении какой либо задачи с помощью компьютера, пользователь практически во всех случаях вынужден пользоваться его периферийными устройствами, которые в свою очередь помогают считывать данные различных носителей и выдают соответствующие результаты. Можно заметить, что обычный пользователь при этом, работает с виртуальными устройствами (не с реальными). Данное понятие способствует абстрагированию знаний пользователя от знания технических тонкостей реальных устройств. Как правило, виртуальное устройство имеет два параметра – имя и значение. Например, предположим, что печатающее устройство имеет имя – prn и назначение – печать. В случае возникновения необходимости, пользователь варьирует его именем. Однако, совсем необязательно чтобы в качестве печатающего устройства был назначен только принтер, им может выступить любое другое не печатающее оборудование. Одним из первых шагов выполнения компьютерной программы, является выполнение процедуры, в котором связываются виртуальное устройство с реальным, вследствие чего, ввод- вывод осуществляется на конкретном физическом оборудовании. Если реальное устройство выйдет из строя, то эту связь не трудно установить изменив переназначения, и ввод-вывод будет производиться на другом устройстве.

В целом, понятие виртуализации применимо во всех областях знаний, в том числе и в области теории механизмов. Чтобы различить реальные звенья и кинематические пары от их виртуальных двойников, всего лишь нужно сопоставить реальный механизм с его составляющей схемой. В данном случае, последнее является виртуальным отображением реального мира – реального механизма. Виртуальные объекты – изображение кинематических пар и звеньев составляющей схемы. На схеме виртуальное звено характеризуется количеством вершин многоугольника, кинематическая пара характеризуется конфигурацией ее значка.

Таким образом, виртуализация дает возможность упростить решение некоторых задач структурного синтеза механизма, освобождая от таких проблем, как расчет и изготовление реальных звеньев механизма, что способствует экономии временных и других затрат, а также повышению концентрации исследователя на анализ исходных данных (структур).

В случае, если составляющая схема будет принята как часть реального мира, то виртуализацию можно использовать повторно, тем самым, создать новые виртуальные объекты для изначальной структурной схемы. Как мы видим, существует возможность проектирования новых алгоритмов, необходимых для решения задач компьютерного синтеза структур механизмов.

Рассмотрим пример, по условиям которого номенклатура и количество звеньев различной сложности определены заранее, и нужно осуществить поиск полного многообразия плоских рычажных механизмов. Существует неограниченное количество вариации структурных схем для одного количества звеньев механизма, которые отличны между собой номенклатурой используемых звеньев и способом соединения их с друг другом. Чтобы уточнить поставленную задачу и намного снизить количество исходных структур, кроме общего числа звеньев, задаются параметры самого сложного звена механизма.

С целью выявления количества звеньев неопределенной сложности, необходимые для создания структурной схемы с заранее заданными параметрами механизма, а также количества кинематических пар, необходимо применить предложенную профессором Л.Т. Дворниковым универсальную структурную систему [1].

+ + + + + (1)

= -

Здесь: n – общее число звеньев;

W – подвижность системы;

m – число наложенных на систему связей;

k – ограничение на классы применяемых кинематических пар;

p_k – число кинематических пар того или иного класса;

τ – количество вершин наиболее сложного звена;

, , , – числа звеньев различной сложности;

У системы может быть несколько целочисленных решений, каждая из которых представляет собой набор чисел, которые в свою очередь отображают собой количество каких либо виртуальных звеньев. Отмечаем, что они виртуальны, ввиду того, что звенья n₁,n₂, … n_i – виртуальны. Также можно заметить, что у них есть имена и только один параметр, которую они вносят в составляющую схему кинематической цепи – число кинематических пар. С точки зрения графического отображения, они преобразятся в реальные звенья на этапе создания составляющей схемы.

Попробуем определить механизм преобразования виртуальных звеньев в реальные, либо выявить их закономерность.

Объект, который состоит из принадлежащих разным звеньям двух сочленяемых элементов, называется кинематической парой. Значит, виртуальное звено более правильно вносит какое либо число кинематических пар. Для удобства, элемент кинематической пары обозначим элкином[2]. Таким образом, число элкинов, привносимые виртуальным звеном и создаваемую структурную схему, определяется индексом в имени виртуального звена.

Общее количество элкинов, имеющиеся в реальном звене, отображает сложность реального звена на структурной схеме.

Общее количество элкинов равна сумме элкинов звена, которые вошли в состав кинематических пар построенной части и привносимые им в структурную схему.

=

В данной формуле выражается механизм преобразования виртуальных звеньев в реальные.

Например, пусть n1 будет виртуальным звеном, привносящий в структурную схему только одну кинематическую пару. Если реальное звено, добавляемое в процессе построения схемы к имеющейся части (фрагмента) а также соответствующее виртуальному звену, образует с ним одну кинематическую пару, тогда общее количество элкинов данного звена будет равняться двум, и это числе определяет, что реальное звено является двухвершинным. (рис.1а)[2]

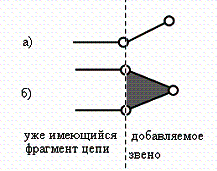
Рис. 1. Превращение виртуальных звеньев в реальные

А если соответствующее виртуальному звену добавляемое реально звено образует с имеющейся частью цепи две кинематических пар, то общее количество элкинов будет равнятся трем, и соответственно реальное звено будет трехвершинным.

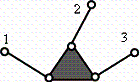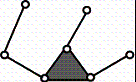А) Б) В)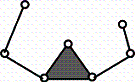

Рис. 2. Варианты схем

На наш взгляд, пример рассмотренный выше является достаточным для аналогичных рассуждений в отношении других виртуальных звеньев.

Однако, в случае образования две кинематических пар в результате добавления реального звена с имеющимся фрагментов цепи, которые не принадлежат одному звену, то мы можем наблюдать образование изменяемого замкнутого контура. Для изменяемости контура достаточно наличия как минимум трех реальных звена между кинематическими парами имеющейся части цепи.

Попробуем вручную построить всевозможные варианты структурных схем шестизвенных шарнирных механизмов. Количество подвижных звеньев 5 и количество неподвижных – 1. Самым сложным и возможным к использованию звеном является треугольное.

Исходные данные выглядят следующим образом: n=5, W=1, m=3, k=5 и τ=3. Подставим их в системе (1), таким образом, получаем всевозможные варианты целочисленных решений. Получить исходные данные возможно вручную, а также с помощью программного обеспечения со встроенным алгоритмом работы, приведенной в формуле (1).

Так, для заданных значений получаем единственное решение: n1 = 4; n2=0.

А) 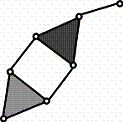Б)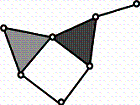

Рис. 3. Схемы с четырехугольным контуром

Следующим шагом будет построение потенциальных вариантов структурных схем. Построение начнем с так называемого τ –угольника, в точности соответствующего реальному звену среди указанных ранее виртуальных звеньев. τ –угольник в данном случае имеет три элкина. Также, есть возможность присоединить к нему три звена соответствующие виртуальным звеньям n1. Принимая во внимание то, что каждое звено присоединяемое к τ –угольнику образует с ним одну единственную кинематическую пару, можно посчитать, что общее количество элкинов присоединяемых звеньев, будет равняться двум, иначе говоря будут поводки и получим следующую часть (рис.2а)[2]. Далее, если добавить к нему четвертый поводок, то получим одну из всех возможных структурных схем (рис.2б)[2]. Другой вариант структурной схемы можно получить путем исключения поводков из любой вершины τ – треугольника.

А)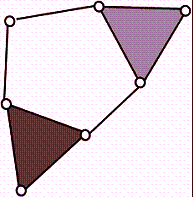

Рис. 4. Схема с пятиугольным контуром

Если же, оставшееся виртуальное звено n1 добавить к фрагменту цепи, причем так, чтобы оно образовало с ним любые две кинематические пары, то в этом случае пятое реальное звено будет с тремя элкинами, т.е. будет треугольным, а у структурной схемы будет изменяемый четырехугольный контур.

Пример такого варианта показан на рисунке 3А[2]. Если убрать правое двухвершинное звено структурной схемы в рисунке 2В[2], а оставшимся пятым звеном n1 соединить звено трехвершинное с двухвершинным левым, тогда получится структура как на рисунке 3Б[2].

Рассмотрим рисунок 2Б[2], уберем среднее двухвершинное звено в структурной схеме и оставшимся пятым звеном n1 соединим вершины 1 и 3 существующего фрагмента и получим структуру с пятиугольным контуром, рисунок 4[2].

В основу порядка работы автоматического синтезатора, который позволяет сгенерировать всевозможные вариации структур плоских рычажных механизмов, с заранее заданным общим количеством звеньев, легла выше описанная технология.

Необходимо отметить, что применение виртуализации, приведенной в данной статье, является одним из важных аспектов при моделировании алгоритмов и компьютерных программ, предназначенных для синтеза структурных механизмов.

СПИСОК ЛИТЕРАТУРЫ

1. Дворников Л.Т. Начала теории структуры механизмов: Учебное пособие/ Новокузнецк, СибГГ-МА, 1994. – 102 с.

2. Степанов А.В. Решение универсальной структурной системы проф. Л.Т. Дворникова Вестн. Куз-ГТУ. 2007, №3.С.43-47.