Комолов В.М., к. физ.-мат наук Латынин Ю.М.

      Украинская инженерно-педагогическая академия. г. Харьков

 

циклоидальные кривые: Новая комплексная форма уравнений

 

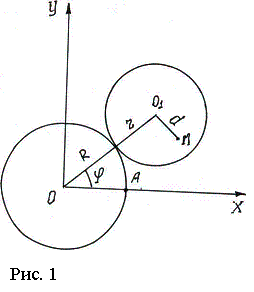       Введение. Важнейшими кривыми на плоскости являются циклоидальные: эпициклоида, кардиоида, астроида и другие. Как правило, они есть трансцендентными и представляют собой фигуры, которые возникают как траектория жестко связанной с кругом радиуса r точки М, находящейся  дальше или ближе от его  центра на расстоянии d, при качении его без проскальзывания по неподвижному кругу радиуса R. Неподвижную окружность называют направляющей, а катящийся по внешней (внутренней) его стороне круг– производящим. Эпициклоида − циклоидальная кривая, получаемая при касании окружностей внешним образом, а гипоциклоида − при их внутреннем касании. При d=r эпициклоиду, гипоциклоиду называют обыкновенными, при  d < r − укороченными, при d > r − удлиненными. Для описания циклоидальных кривых используют параметрическое их представление, прямоугольную или полярную     систему координат.

 

Основная часть. Представление их на комплексной плоскости позволит получить компактную форму уравнений, увидеть общие и специфические закономерности их поведения. Поместим начало координат в центр неподвижного круга радиуса  R (рис. 1.), по которому катится диск радиуса r. В исходном положении производящий круг касается неподвижного в точке А, через которую проходит ось абсцисс, а угол  φ –  образован осью ОХ и соединяющим центры кругов радиусом ОО1. Параметр m=r/R, от которого зависит форма циклоидальных кривых, называют модулем.

     I. Параметрические уравнения для эпициклоид следующие [1,2]:

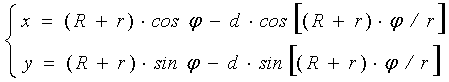                                   (1)                                             

Умножим на мнимую единицу i левую и правую части  второго уравнения  и просуммируем  его с первым:

                           z=x+iy= (R+r)∙eiφ − dei∙=

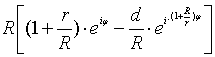      =  =R[(1+m)∙eiφ − s∙ei∙],                     (2)

где параметр s=d/R .               

Применим обобщенную теорему сложения  [3] к выражению в квадратных скобках, которое  есть разность двух комплексных величин, и получим:

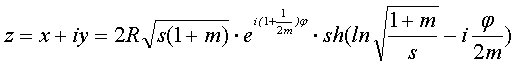                     (3)

 Введем комплексную переменную       w =                                   (4)

 и запишем уравнение (3) иначе

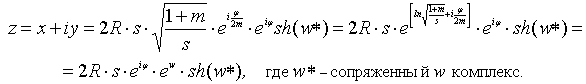     (5)

Введем нормированную переменную Z, так как R∙s=d:    Z=X+iY= 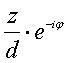    (6)

и уравнение (5) представим в виде:     .      (7)

Модуль  |z| и аргумент arg z  в формуле (5) соответственно равны:

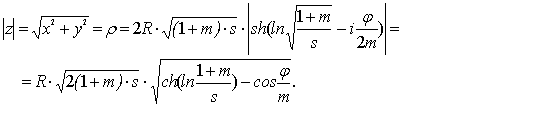             (8)                                           

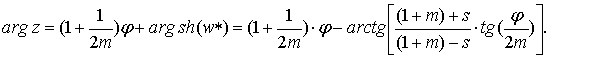   (9)   

  II. Аналогично преобразуем параметрические  уравнения гипоциклоид [1,2]:                                       

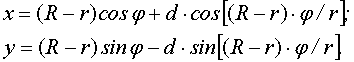                                                  (10)

 В комплексной форме:

      .    (11)

 Применим обобщенную теорему сложения [3] и из (11) получим:

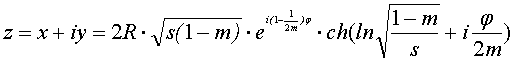             .    (12)

Аналогично (4) введем комплексную переменную v: 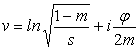.Тогда:  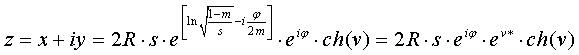, (13)

где v* − сопряженный v комплекс. Используя (6), получим уравнение гипоциклоид:                                                                       (14)

Модуль  |z|  и аргумент arg z  в (13) равны соответственно:

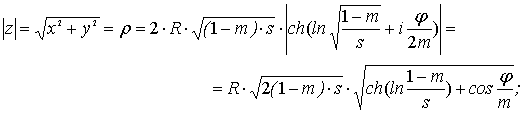               (15)

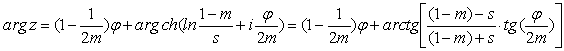.      (16)

Уравнения эпициклоид (5), (7÷9)  и  гипоциклоид (14÷16) подобны. Это позволяет единообразно исследовать их общие и частные случаи.  

III. В случае      d=r, s=d/R=r/R=m, R∙s=R∙m= r                                     (17)

уравнение обыкновенной эпициклоиды имеет вид:

   где ,   (18)

а обыкновенной гипоциклоиды:

      где   .   (19)

    IV. При R=r, т.е. m=1 и d≠r каждая эпициклоида являет собой улитку Паскаля. В этом случае

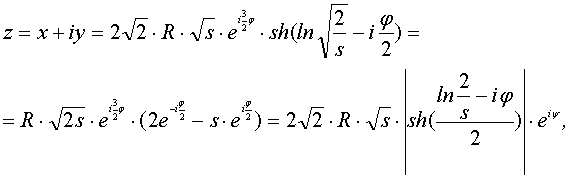      (20)

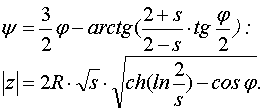где                                                             (21)

Уравнение обыкновенной эпициклоиды при  d=r, s=d/R=r/R=m=1, называемой кардиоидой [1,2 ], имеет следующий вид:

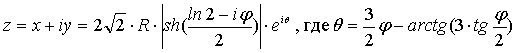            (22)

В отличие от представления улитки Паскаля и кардиоиды в математической литературе, в данном графическом представлении фигуры в координатах (х,у) повернуты на угол π.  

      V. При r/R=1/2, т.е. при m=1/2, как удлиненная, так и укороченная гипоциклоиды представляют собой эллипс с центром в точке О (рис.1). При этом

                                    

                                  

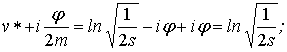
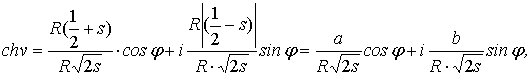
 где    a,b – полуоси эллипса:

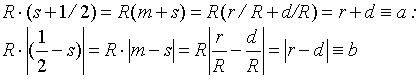                                (23)

Уравнение эллипса на комплексной плоскости:   

                         z=x+iy= R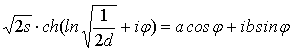  .                (24) Соотношение (24) без труда трансформируется в известное представление:

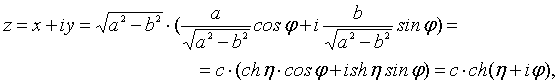
где с − половина фокусного расстояния эллипса.

      VI. Астроида является частным случаем обыкновенной гипоциклоиды при r:R=1:4 , т.е. m=r/R=1/4; d=r; s=d/R=r/R=m. Итак, для астроиды m=s=1/4;    

                                     

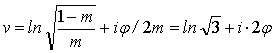
              z=x+iy=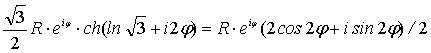   (25)

 Уравнение астроиды:

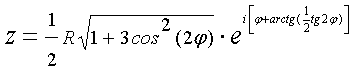                            .                        (26)

 Кривая Штейнера (дельтоида) − частный случай обыкновенной гипоциклоиды, которой соответствует  r/R=1/3, т.е.  m= r/R=1/3; d=r; s=d/r=r/R=m ;

                                    v=ln+ 3iφ/2;  ev*∙eiφ= .      

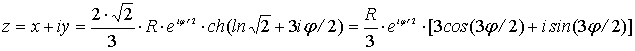
Уравнение дельтоиды: 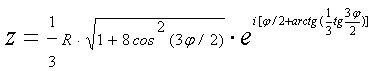        (27)

      VII. Соотношения для  циклоидальных кривых преобразуем к такому  виду, который позволит анализировать их внутреннюю структуру. В уравнении эпициклоиды (3) преобразуем аргумент гиперболического синуса:

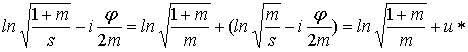                             (28)

 где u*− сопряженный u комплекс, а       .                     (29)

 Тогда выражение гиперболического синуса в формуле (3) примет вид:

   (30)

а уравнение эпициклоиды (3) станет следующим:

    .                 (31)

Представим последнее выражение в виде суммы двух слагаемых: z= z1 +z2,

где               ,                (32)

причем:

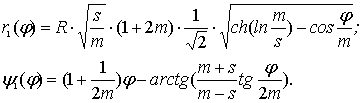                                                  (33)

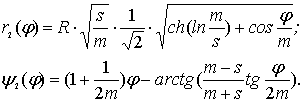                                                               (34)

    Применим аналогичные преобразования для уравнения гипоциклоиды.  Гиперболический косинус в формуле (12) примет вид:

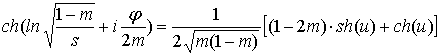                     ,           (35)

а ее уравнение будет следующим:

         .               (36)

Представим последнее выражение, как сумму двух слагаемых z= z1 +z2,

где                    ,                 (37)

причем:

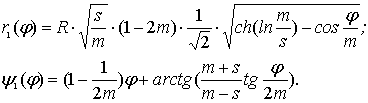                                                (38)

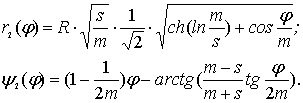                                                             (39) 

Из анализа соотношений  (33÷34), (38÷39) вытекает вывод: циклоидальные кривые в комплексном представлении есть суперпозиция элементарных замкнутых кривых в форме «лепестков роз» или им подобных. Для обыкновенной  эпициклоиды, когда  m=s , формулы (33÷34) упрощаются:

         

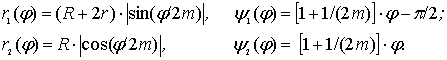
Эти кривые имеют многолепестковую структуру, а графики r1(φ),  r2(φ)           для m=1представлены на рис.2.

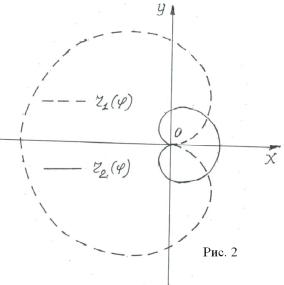VIII. Пусть уравнение циклоидальной кривой задано комплекснозначной функцией: z(φ)=x(φ)+iy(φ). Радиус кривизны ее определяется формулой [1]:

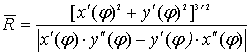      .  (40)

Так как а               

              ,

||=

=, то подставив эти выражения в (40), получим соотношение для :

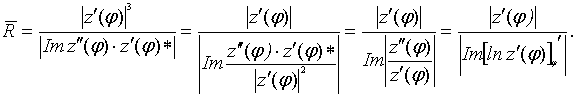   (41)

    Пример.  Расчет радиуса кривизны эпициклоиды.  Вычислим величины, которые входят в (41). Тогда из (3) после ряда преобразований получим:                                 

                                                             (42)

                           и               .                           (43)

Преобразуем выражение знаменателя в (41) таким образом:

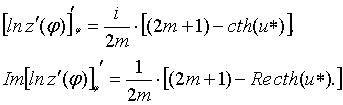
Для расчета    воспользуемся формулой (38) из [4]. Тогда

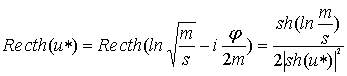                                                        (44)

 и  соотношение для радиуса кривизны эпициклоид имеет вид:

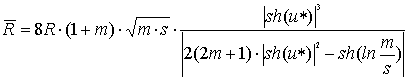             .                             (45)

Подставим в (41) выражение

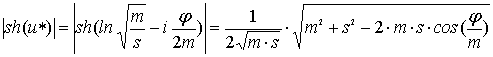                        (46)

 и получим для  радиуса кривизны   эпициклоид  соотношение:

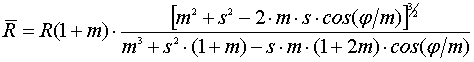                  ,         (47)

которое совпадает с приведенным  в [1]. В случае обыкновенной эпициклоиды,

т. е., когда m >0  и s=1, получаем:

                                    .

Аналогичные соотношения могут  быть получены и для гипоциклоиды.

Выводы: Использование комплексного переменного и обобщенной теоремы сложения позволило объединить  уравнения, описывающие циклоидальные кривые,  проследить общность и специфику их поведения и,  в частности, исследовать  внутреннюю структуру кривых.

         Список литературы:

1.  Бронштейн И.Н., Семендяев К.А. Справочник по математике  для инженеров и учащихся втузов. -13-е изд..- М.: Наука, гл. ред. физ.-мат. лит. 1986.- 544 с.

2. Математическая энциклопедия: гл. ред. И.М. Виноградов, М.: Советская энциклопедия, 1984, т.1-5.

 3. Комолов В.М. Обобщение теорем сложения для тригонометрических функций. Materials of the X International scientific and practical conference «Modern european science»,-2014.Vol.15. Mathematics. Physics. Sheffield. Science  and Education LTD.- P.38-42.

  4. Комолов В.М., Латынин Ю.М. Обобщенная формула тангенсов: примеры применения. Materials of the X1 International Research and Practice сonference «Science and Civilization-2015», Vol.23, Mathematics. Modern information technologies», Sheffield. Science  and Education LTD.- P.24-30

  

.