Математика/4. Прикладная математика

К.ф.-м.н., доцент Батыров Б.Е.

Северо-Казахстанский государтвенный университет им М.Козыбаева, Казахстан

О группе симметрии квадрата

Целью настоящей работы является изучение группы симметрии квадрата посредством реализации подстановок длины 4.

Пусть дан квадрат на плоскости. Обозначим вершины квадрата соответственно через 1, 2, 3 и 4. Рассмотрим симметрию квадрата .

Симметрия квадрата - движение плоскости, переводящее квадрат в себя. Движение плоскости - преобразование плоскости, сохраняющее расстояние.

Обозначим через множество симметрий квадрата . Сначала составим список симметрии квадрата. Это - 4 поворота: на , , , , и 4 осевые симметрии: [1].

1 2

2

43

Тогда список симметрии квадрата посредством подстановок длины 4 можно реализовать следующим образом:

–поворот на «», –поворот на «»,

–поворот на «», – поворот на «».

–симметрия относительно оси , - симметрия относительно оси , - симметрия относительно оси , - симметрия относительно оси .

Таким образом, множество симметрии квадрата имеет вид

.

На множестве определим умножение симметрий квадрата как их последовательное выполнение. Например, произведение есть последовательный поворот квадрата сначала на «», потом - на «». В итоге получаем поворот квадрата на «», т.е. элемент . С другой стороны, произведение есть умножение подстановок и .Таким образом,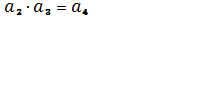 и можно найти произведение всех элементов множества . Результаты произведений элементов множества занесем в таблицу Кэли.

Здесь мы предварительно вычислили попарно произведение всех элементов множества .

Первая строка и первый столбец таблицы называются соответственно главной строкой и главным столбцом. Все элементы, находящиеся ниже главной строки и правее от главного столбца, представляет собой квадрат. Следует обратить внимание на то, что элементы, расположенные в каждой строке и в каждом столбце квадрата, разные. Такой квадрат называют латинским. Это означает, что введенная операция умножения подстановок замкнута на множестве . Тогда справедливо следующее утверждение.

Теорема. Множество относительно умножения подстановок образует группу.

Доказательство. Проверим выполнимость условий определения группы.

1. Ассоциативность умножения подстановок из , т.е. равенство

следует из таблицы.

2. Существование единичного элемента на множестве видно из таблицы. Действительно, из первой строки и из первого столбца латинского квадрата видно, что существует элемент , что для любых

3. В каждой строке и в каждом столбце латинского квадрата находится единичный элемент . Элементы главной строки и главного столбца, на пересечении которых стоит элемент , являются взаимно-обратными. Например, из таблицы видно, что элементы и являются взаимно- обратными элементами. Остальные элементы сами с собой - взаимно - обратные.
Таким образом, доказано, что множество образует группу.

Литература:

Кострикин А.И. Введение в алгебру. Основы алгебры. М.: МЦНМО, 2012.