Математика /4. Прикладная математика

Д.ф-м.н. Рыльцев Е.В¹., к.т.н. Калашникова Л.Е²., К.Е. Лысак,

1. Межрегиональная академия управления персоналом, г.Киев

2. Киевский национальный технический университет Украины «КПИ», г.Киев

Доказательная база некоторых положений ортогональной аксонометрии

Освоение учебной дисциплины "ортогональная аксонометрия" осложняется тем, что её исходные посылки подаются, чаще всего, в декларативной форме или, в лучшем слу-чае,со ссылкой на труднодоступные источники [1-5]. Настоящим мы постарались испра-вить сложившуюся ситуацию,базируясь исключительно на правилах элементарной гео-метрии с тригонометрией [6, 7].

Как известно, аксонометрия - это набор способов отображения на плоскости (в двумерном пространстве) какого-либо природного тримерного объекта. Его положение в пространстве и его размеры определяются системой декартовых координат. При этом плоскость аксонометрической проекции "сечёт", в общем случае, прямоугольный координатный тригранник произвольно,что выражается в соотношении длин его коорди-натных осей: OZ ≠ OY≠ OX (рис.1).

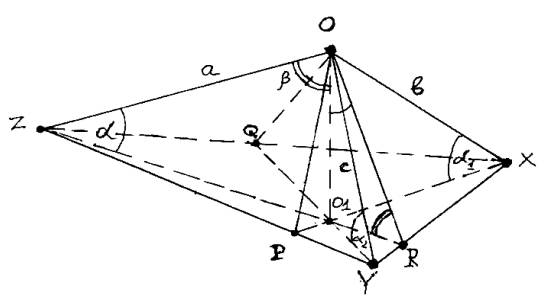
Рис.1. Ортогональная триметрическая аксонометрия [cos²a_i = (n/m)_z,y,x].

В результате образовавшийся треугольник следов – ∆ ZYX может принимать произвольную форму. То есть, его стороны могут быть связаны неравенством – ZY ≠ ZX ≠ YX. Это вид проекции – аксонометрическая триметрия. Единственным ограничивающим условием в случае ортогональной аксонометрии является направление отрезка ОО₁ – перпендикуляра из начала координат О на аксонометрическую плоскость проекции ZYX, чем, собственно, и задаётся направление проецирующих лучей в данном виде аксонометрического отображения.

Из рис.1 следует, что, поскольку плоскости ZOR, YOQ, XOP проведены так, что они перпендикулярны плоскости ZYX,то именно углы OZR, OYQ и OXP определяют коэффициенты искажений (К) по координатным осям OZ, OY, OX. То есть, К_z= cosα, К_x= =cosα₁, К_y= cosα₂ . Но так как углы α, α₁ и α₂ неодинаковы, то К_z ≠ К_y ≠ К_x. Именно этот факт соответствует триметрической аксонометрии. Справедливым остаётся и обобщающее уравнение [1–5]:

К_x² + К _y² + К_z² = 2

Чтобы выявить в этом случае некоторые количественные угловые соотношения рассмотрим ∆ZOR, образованный в результате сечения координатного тригранника плоскостью проходящей через координатную ось OZ и перпендикуляр ОО₁ к аксонометрической плоскости проекций ZYX .

Названый треугольник состоит из двух других треугольников – DOZO₁, DORO₁, что можно выразить так: DZOR = DOZO₁ + DORО₁.

Поскольку соответствующие углы обозначеных треугольников взаимно равны (рис.1), то это значит, что ΔZOR ~ ΔOZO₁ ~ ΔORO₁.

Тогда можно записать:

(O₁Z )/(OZ) = (OZ)/(ZR). То есть, (OZ)² = (O₁Z)/(ZR).

Если принять, что (O₁Z)/(ZR) = n/m (назовём эту пропорцию "высотной"), то (ОZ)² = n/m (ZR)·(ZR) или же (OZ)²/(ZR)² = n/m.

Но (OZ)/(ZR) = cosα. Значит cos²α = n/m = K²_z. Величины K_y и K_x можно получить аналогичным путём , рассматривая треугольники ∆YOQ и ∆XOP.

Тогда значения К_z,x,y== cos (a;a₁;a₂) = [(n/m)_z,x,y]^1/2 при условии их взаимного неравенства.

В случае изометрической аксонометрии её исходным параметрическим соотношением служит равенство: a = b = c (рис.2).

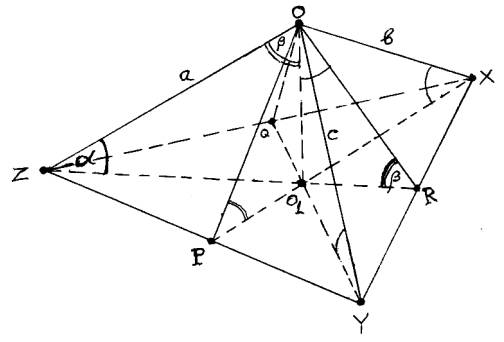
Рис.2. Ортогональная изометрическая аксонометрия [cos²a = (n/m)_z,y,x=2/3].

Отсюда следует, что ZY = YX = XZ.

То есть, треугольник ∆ ZYX – равносторонний треугольник. Известно [5,6], что в таком треугольнике точка О₁ делит его высоты (биссектрисы, медианы) в отношении (ZO₁)/(ZR)= (YO )/(YQ) = (XO )/(XP) = n/m = 2/3.

Если учесть, что a = a₁ = a₂ (это очевидно из рис.2), и соответственно:

К_z = К_y = К_x = К_z,y,x , то K_z,y,x = (2/3)^1/2 » 0,82.

Тогда a_i » 35°; b_i » 55° при условии, что a_i + b_i = 90°.

Угловые соотношения аксонометрической диметрии удобно рассматривать в процессе эволюции "изометрического" координатного тригранника (рис.2). Такую эволюцию можно представить в двух вариантах. Один из них (рис.3) предполагает, что "высотная пропорция" - n/m варьирует следующим образом: 2/3 £ n/m ® 1. Тогда угол a в триграннике изменяется в диапазоне: 35° ³ a > 0°.

Другой вариант эволюции изометрического координатного тригранника реализуется (рис.4) в случае, при котором "высотная пропорция" стрeмится к 0 от своего "изометрического" значения, то есть, 0 ¬ n/m £ 2/3. Тогда угол b принимает значения в диапазоне 0°¬ b £ 55°.

Первый вариант эволюции изометрического координатного тригранника может быть реализован двумя cпособами. Один из них – это, когда точка Z → ∞. Тогда сторона тригранника a = OZ→∞, стороны b = c и XY остаются нeизменными, отрезок ОО₁→OR= const, координатная ось OZ стремится к параллельности со следом ZR плоскости ZOR и, наконец, когда стороны XZ, YZ и OZ становятся взаимно параллельными.

Второй способ реализации того же варианта эволюции изометрического тригранника (рис.2) возможен, если (b =c) → 0 при a = OZ = const (рис.3).

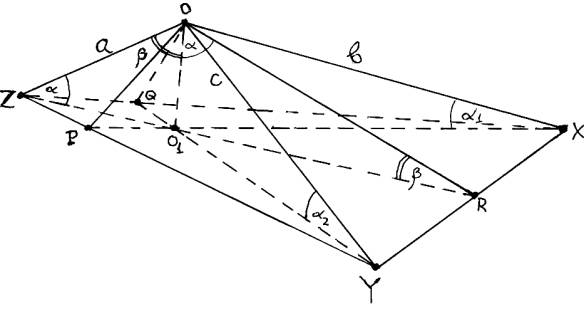
Рис.3. Ортогональная аксонометрическая диметрия при 2/3 £ (n/m)_ZR < 1.

Тогда OO₁ → OR → 0; XY→ 0; OZ→ ZR, а (XZ = YZ) → OZ.

Оба указаные способы первого варианта эволюции имеют следствием (рис.3): O₁R→ 0; 55°»b→ 90°; 60°= ÐYZX → 0; 120° = (ÐYO₁X=ÐPO₁Q)→180°; 120° = (ÐZO₁X=ÐZO₁Y)→90°; 60° = (ÐZYX=ÐZXY)→90°; (∆OO₁X =∆OO₁Y)→ →(∆ORX=∆ORY).

Из последней записи следует: 35° » (a₁ = a₂) → (Ð OXY = Ð OYX) = 45°. То есть, при таком варианте эволюции аксонометрической изометрии (рис.2) мы получаем аксонометрическую диметрию (рис.3), при которой коэффициенты искажений по координатным осям изменяются в диаппазонах: 0,82 £ К_z< 1 и 0,82 ³ (K_x = K_y) > 0,71.

Второй вариант эволюции изометрического координатнолго тригранника (рис.2) в аксонометрическую диметрию (рис.4), как и первый вариант, также может быть реализован двумя способами. Один из них предполагает следующие этапы: точка R→ ∞; (b= c) = (OX = OY) → ∞ при a = OZ = const и OO₁ → OZ = const. При этом следы сечений OR и ZR стремятся ко взаимной параллельности так же, как и стороны OX = OYстремятся к параллельности со сторонами ZX = ZY.

Второй способ реализации второго варианта эволюции изометрической формы координатного изометрического тригранника (рис.2) в диметрию предполагает процессы (рис.4): ( a = OZ ) → OO₁ → 0; ( ZX= ZY ) → ( OX = OY ) = (b=c) = const. При этом ZR → OR → O₁R.

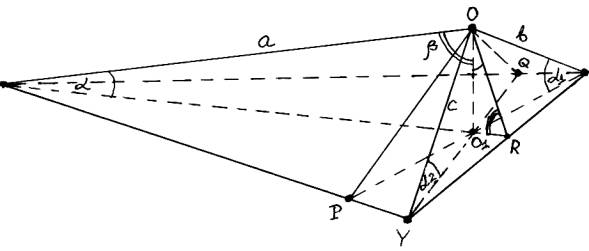
Рис.4. Ортогональная аксонометрическая диметрия при 0 < (n/m)_ZR £ 2/3.

Выше обозначенные переходы имеют следствием (рис.4): 35°£a®90°; 35³ (a₁ =a₂) → 0; 60° = ÐYZX→ÐYOX = 90°; 120°= (ÐXO₁Y = ÐPO₁Q) → 90^°; 45° = (ÐOZX = ÐOZY) → 90°; 45° = (ÐZXO = ÐZYO) → 0; 60° = (ÐZYX = ÐZXY) → (ÐOYX = ÐOXY) = 45; 120°= (ÐZO₁Y = ÐZO₁X) →135°.

Полученная таким образом аксонометрическая диметрия характеризуется коэффициентами координатно-осевых искажений, изменяющимися в интервалах: 0<K_z££ 0,82 и 1 > (K_x =K_y) ³ 0,82.

Найденныве интервалы изменений коффициентов искажений по координатным осям аксонометрической ортогональной диметрии можно получить такжe и из формул функциональной взаимозависимости соответствующих углов в прямоугольном координатном тетраэдре (рис.3; 4). А именно, cos a_1;2=[(1+sin²a)/2]^1/2 и cosa=(2)^1/2sina_1;2. Эти формулы выведены, исходя из свойств треугольников: D OO₁Y; D OO₁R; D O₁RY;D ORY и D OZR (рис.3;4). Однако результаты таких формальных расчётов теряют структурную наглядность динамики изменений коэффициентов искажений (K_z,y,x) по сравнению с результатами анализа эволюционных изменений прямоугольного координатного тетраэдра аксонометрической изометрии, представленного на рис.2. Действительно, если принять во внимание, что изменение коэффициентов искажений K_z,y,x во всём своём диапазоне развивается за четверть периода (0°< a < 90°) косинусоидальной гармоники при 0 < n/m < 1, то от 0 до 1 изменяется лишь коэффициент K_z. Коэффициенты же K_y = K_x изменяются при этом в интервале - (1; 0,71). А именно, eсли 0 < a_1,2 £ 35° и 90°> a ³ 35° при 0 < n/m £ 2/3, то 1 > (K_y = K_x ) ³ 0,82 (рис.4).

В случае же 35°£ a_1;2< 45° при 35°³ a> 0° и 2/3 £ n/m< 1 имеем 0,82³ (K_y=K_x ) > 0,71 (рис.3).

Таким образом, в настоящем изложении использование предложенного здесь параметра - "высотная пропорция" позволяет представить материал об ортогональной аксонометрии в достаточно наглядной, компактной и последовательной форме, что облегчает его освоение.

Литература:

1. Чалый А.Т. Курс начертательной геометрии. - М.-К.: МАШГИЗ, 1952.-279 с.

2. Колотов С.М. Начертательная геометрия. - К.: "Вища школа", 1975. -261 с.

3. Виноградов Н.Н. Начертательная геометрия. - Минск.: "Вышэйшая школа", 1977.-368 с.

4. Фролов С.А. Начертательная геометрия. - М.: "МАШИНОСТРОЕНИЕ", 1978.

- 240 с.

5.Михайленко В.Є., М.Ф.Євстіфеєв, С.М.Ковальов Нарисна геометрія. - К.:"ВИЩА ШКОЛА", 2004. - 300 с.

6. Нікулін О.В. Геометрія. Поглиблений курс. -К.: "ПЕРУН", 1999. - 349 с.

7. Жолдак М.І., Грохольська А.В., Жильцов О.Б.Математика (тригонометрія, геометрія, елементи стохастики). - К.: МАУП, 2004. -456 с.