Математика /5. Математическое моделирование

К.ф.-м.н. Володченков А.М.

К.ф.-м.н. Скородулина Е.Ю.

Смоленский филиал ФГБОУ ВПО «РЭУ им. Г.В. Плеханова»

Основные задачи теории упругости для анизотропных тел в стохастической постановке

Основные задачи теории упругости в анизотропном случае сводятся к системам краевых задач [3]. Например, граничные условия первой основной задачи

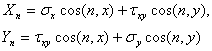(1)

можно записать следующим образом:

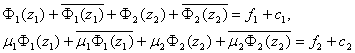(2)

где - неизвестные аналитические функции обобщенных комплексных переменных , ,

, - корни определенного характеристического уравнения. Будем рассматривать неравные корни, примем

.

Общее выражение для компонентов напряжения можно получить, используя аналитические функции

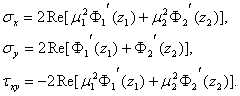(3)

Перенесем решение задачи (2) на единичную окружность. Для этого рассмотрим функции как функции обычных переменных

(k = 1, 2),

определенных в областях D₁, D₂

.

Пусть функции конформно отображают области D, D₁, D₂ соответственно на внутренность единичного круга. Обозначим соответствующие обратные функции . Краевое условие (2) преобразуется к следующему виду:

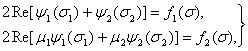(4)

где

(5)

Выразим переменные через

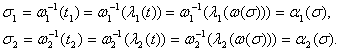(6)

Здесь под точками t, t₁, t₂ понимаются соответствующие точки контуров L, L₁, L₂. Функции отображают окружность на себя. С учетом обозначений (6) перепишем краевые условия (4):

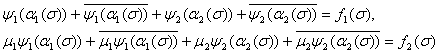(7)

Поскольку в общем случае не является граничным значением аналитической функции, то функции , в свою очередь, не будут аналитическими в точке t.

Задача (7) была подробно исследована в работе [2]. Решение основывалось на свойствах интеграла типа Коши и уравнений Фредгольма 2-го рода. При использовании интеграла типа Коши представляют достаточно «жёсткие» требования к заданным функциям и к области, занятой телом.

На практике встречаются случаи, когда форма тела и внешние нагрузки имеют случайную составляющую. Это может приводить к тому, что для реализаций случайного вектора краевые условия (7) не будут выполняться.

В работе предлагается метод, основанный на использовании стохастической теории потенциала, который позволяет «убрать» случайную составляющую из краевых условий (7).

Дадим определение χ-аналитической функции [3].

Определение. Функция в области D, ограниченной контуром Г, называется χ-аналитической, если для всех и всех открытых множеств W, для которых :

(8)

Здесь M(f) – математическое ожидание случайной функции f;

- момент первого выхода двумерного броуновского процесса из множества W.

Функции и связаны между собой соотношениями Коши-Римана.

Приведём стохастическую постановку первой основной задачи теории упругости для анизотропного однородного тела.

Требуется определить χ-аналитический вектор по краевому условию.

(9)

Здесь - первый момент выхода случайного броуновского процесса из единичного круга .

Соотношение (9) выполняется почти наверное. Математическая модель (9) учитывает, что нагрузки, т.е. функции и форма тела, т.е. функции могут содержать случайную составляющую.

Приведём соотношение (9) к детерминированному виду.

Перепишем краевые условия в следующем виде:

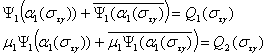(10)

Здесь

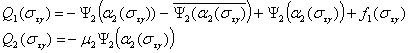
Системы (10) представляют собой две стохастические задачи Дирихле относительно χ-аналитических функций.

Решение этих задач даётся формулой [3].

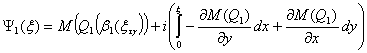(11а)

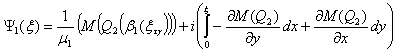(11б)

Приравнивая выражения (11а) и (11б) получим детерминированное условие для определения функции .

Для перехода к краевым условиям воспользуемся соотношениями:

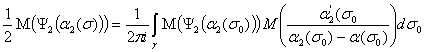(12)

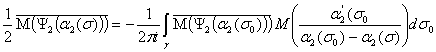
Для определения функции из соотношений (11а) и (11б) с учётом (12) получим краевое условие:

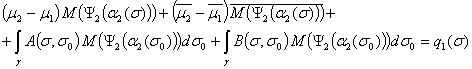(13)

Здесь , - известные ядра Фредгольма, - заданная функция класса Гёльдера, - краевое значение функции .

Явный вид ядер и свободного члена в краевом условии (13) приведён в работе [2].

Краевая задача (13) сводится к уравнению Фредгольма 2-го рода. Таким образом, первая основная задача теории упругости для анизотропного тела в стохастической постановке сведена к детерминированной краевой задаче (13).

Заметим, что ядра и имеют достаточно сложный вид. Однако в ряде случаев решение задачи (9) существенно упрощается.

Рассмотрим бесконечную упругую плоскость, обладающую прямолинейной анизотропией, ослабленную эллиптическим отверстием. Пусть плоскость испытывает на бесконечности растяжение с усилием Р, составляющим угол α с осью ОХ.

Напряжённое состояние на бесконечности определяется соотношениями:

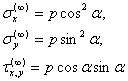
При этом контур свободен от усилий. Свободные члены краевых условий (10) примут вид:

,

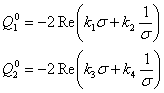где - постоянные, зависящие от формы отверстия и упругих свойств материала.

Согласно полученным в работе результатам

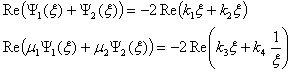
Отсюда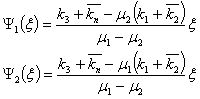

Переходя с единичной окружности на контуры и получим

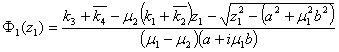(14)

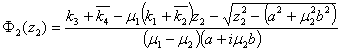
Функции напряжений определим по формулам:

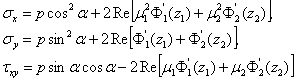(15)

Выражения (14), (15) совпадают с результатами, полученными классическими методами.

Литература:

1. Мусхелишвили Н.И. Сингулярные интегральные уравнения. – М.: Наука, 1966, 511 с.

2. Гахов Ф.Д. Краевые задачи. – М.: Наука, 1977, 640 с.

3. Лехницкий Г.С. Теория упругости анизотропного тела. – М.: Наука, 1977. – 446 с.

4. Редкозубов С.А., Юденков А.В., Володченков А.М. Моделирование процесса линейной деформации упругого однородного тела с помощью бианалитических функций. //Вестник Чувашского государственного педагогического университета имени И.Я.Яковлева. №1(48), 2006, с.128-134

5. Юденков А.В., Володченков А.М. Основные задачи теории упругости тел с прямолинейной анизотропией в стохастической теории потенциала //Ученые записки: электронный научный журнал Курского государственного университета . 2013. № 2 (26) [Сайт]. URL: http://scientific-notes.ru/pdf/030-002.pdf