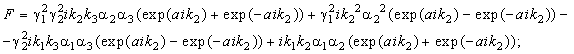Reshetnyak S. O., Stadnichenko I. O.

National technical university of Ukraine “Kyiv Polytechnic Institute”

Peremohy av., 37, Kyiv, 03056, Ukraine

Three-component ferromagnetic environment as a basis for spin-wave optical devices

Statement of the problem

The great interest has the study of reflective properties of spin waves from ferromagnetic environment. This is one of the modern ways of researches in the physics of ferromagnetic environment. In this paper will be presented the basic formulas to obtain complex reflection coefficient of spin waves from the three-component ferromagnetic environment. Also will be discussed the graphic dependence of reflection coefficient from material parameters, and frequency, external magnetic field.

Solving

Consider the system, which consist of three parts, collision planes are parallel to the plane yz. The first and the third (along the direction of the axis x) part is a homogeneous semi-infinite uniaxial ferromagnet, and among them is N- ferromagnetic layer with modulated exchange interaction constants a, uniaxial magnetic anisotropy b and saturation magnetization M₀. The layers are parallel to the plane yz and has a thickness a1 and a2. The values of a, b і M₀ equal to values , , and , , and in appropriate layers. Easy axis is parallel to the direction of the external constant homogeneous magnetic field and the axis z.

We need to get the equation for the magnetization dynamics of spin waves, which will be propagate over the surface of the material. To do this, write down the Landau-Livshitz excluding dissipative member:

Referring to the linear perturbation theory, the external constant magnetic field is represented as , where - the spatial energy density of magnet.

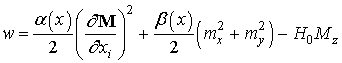Based on the formalism of spin density distribution of magnetization represented as:

Through linearization of equations for the magnetization, we obtain the next solutions:

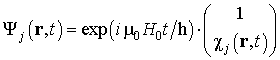Using the condition fixing spins on the surface, we obtain the final equation for the magnetization dynamics:

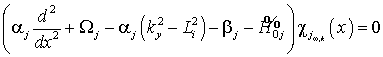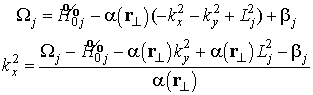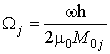, w – the frequency, – wave vector, .

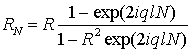- amplitude of the reflection of spin waves from three-component ferromagnetic environment with layers.

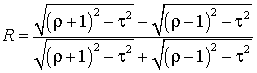- amplitude of the reflection of spin waves from a semi-infinite three-component ferromagnetic environment.

Boundary conditions for non-ideal interaction between layers:

, ,.

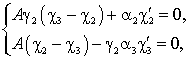Comparing the incident wave function, the reflected waves - , and the wave that passed through some period - , where , and - the wave vectors of the incident (covered), passing and the reflected, passing and the reflected wave respectively, we arrive to the expressions for the amplitudes of reflection and passage of spin waves:

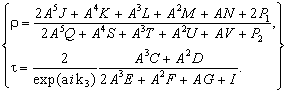
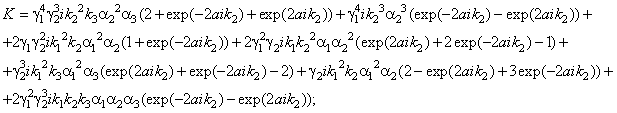
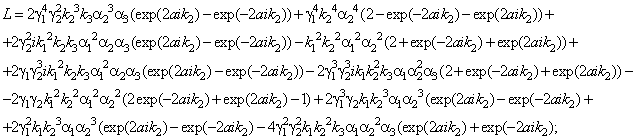
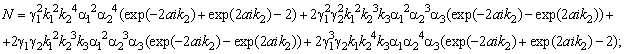
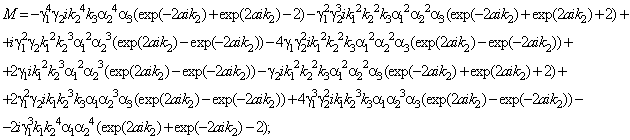
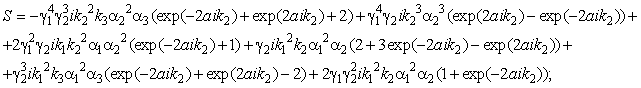
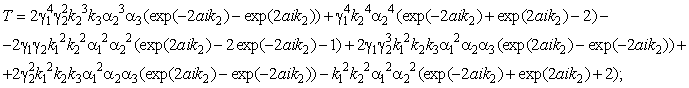
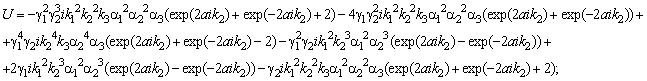
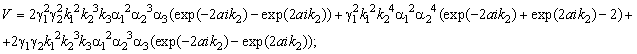
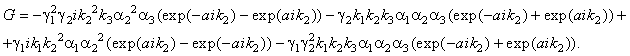
Discussion of results

We had got the expression for the complex reflection coefficient of spin waves from three-component ferromagnetic environment, and the complex transmission coefficient for three-component ferromagnetic environment having a finite number of layers.