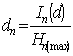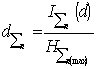METHODS OF CALCULATION THE INFORMATION ANALYSIS OF QUALITY OF TECHNOLOGICAL PRODUCTS AND PROCESSES

SUGGESTED BY SHANNON

S.Sh.Kazhikenova, S.N.Shaltakov

Quantitative estimations of sense and value of the information can be made for the information analysis of quality of technological products and processes of their reception only after the preliminary agreement about what precisely in each concrete case has value and sense for the considered phenomena. Methods of calculation the information suggested by Shannon allow to reveal a ratio of quantity of the predicted information (that is formed by the certain rules) and quantities of the unexpected information which cannot be predicted beforehand, and thus to enable to define a qualitative and quantitative estimation of the certain technological circuit. As a probability of detection of the main element of technological system it is possible to accept its maintenance in a product, expressed in shares of unit.

For example, let’s examine the maintenance of a considered chemical element, in our case - copper, in products of technological repartition. Also for probability of detection it is possible to take the maintenance of suitable fraction (remnants, briquettes) in a corresponding product. The same concerns the process of extraction of an element in this or that product, as in this case a parameter of extraction is equal to a probability of transition of the given element from one condition of system into another. These both parameters - the maintenance and extraction - can be equally used for an estimation of quality of a product or technological repartitions.

Let's show how quality of technological products and the technological operations resulting in reception of these products is estimated by results of technological repartitions copper-liquating manufactures on Zhezkazgan and Balkhash mining-metallurgical combines (table 1) and CODELCO concern's (table 2).

Table 1 - The maintenance of copper in products on Zhezkazgan and Balkhash mining-metallurgical combines

Repartition	The level.	The name	Maintenance %	Average value
				%	д.е.
Extraction	0	Ore	0,5-1,2	0,85	0,0085
Enrichment	1	A concentrate	5,5-40	22,75	0,2275
Melting	2	Stein	40-55	47,50	0,4750
Converting	3	Draft copper	98,6-98,9	98,75	0,9875
Fire refinement	4	Anodic copper	99,2-99,5	99,35	0,9935
Electrolyte refinement	5	Cathode copper	99,9-99,99	99,95	0,9995

Table 2 - The maintenance of copper in products on CODELCO mining-metallurgical combines

Repartition	The level.	The name	Maintenance %	Average value
				%	д.е.
Extraction	0	Ore	1,0-2,0	1,5	0,0150
Enrichment	1	A concentrate	8,0-50,0	29,0	0,2900
Melting	2	Stein	55,0-58,0	56,5	0,5650
Converting	3	Draft copper	97,0-98,5	97,75	0,9775
Fire refinement	4	Anodic copper	99,8-99,85	99,83	0,9983
Electrolyte refinement	5	Cathode copper	99,9-99,99	99,95	0,9995

For accounting of a various degree of unexpectedness (probability) of events K. Shannon has suggested to use probabilities' function of entropy borrowed from statistical physics, resulted as follows [1]:

,

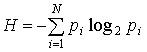where – is a probability of detection of any homogeneous element of system in .

If is a probability of detection of a controllable element then unexpectedness or uncertainty of this detection is equal to .

In our variant of estimation this uncertainty will be expressed as:

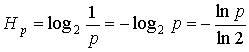. (1)

Before the publication of K. Shannon's theory R.Hartly has suggested to define quantity of the information under the formula [2]:

, (2)

where , - number of levels, - length of a code

The determined component of the information is defined by equality:

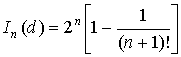Bit/el.

The system determined component is equal:

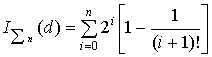Bit/el.

Having defined degrees of determination and ineradicable stochasticity at each level of technological system under formulas [3]:

, ,

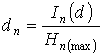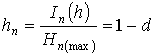let's analyze the received results of the carried out calculations which are submitted in table 3.

Table 3 - Settlement information-entropy characteristics of technological repartitions in hierarchical system for ,

0	0	1,0	0	0	1,0	0
1	1,0000	2,0	0,5000	1,0000	3,0	0,3333
2	3,3333	4,0	0,8333	4,3333	7,0	0,6190
3	7,6667	8,0	0,9583	12,0000	15,0	0,8000
4	15,8667	16,0	0,9917	27,8667	31,0	0,8989
5	31,9556	32,0	0,9986	59,8222	63,0	0,9496
6	63,9873	64,0	0,9998	123,8095	127,0	0,9749
7	127,9968	128,0	1,0	251,8063	255,0	0,9875
8	255,9993	256,0	1,0	507,8056	511,0	0,9937
9	511,9999	512,0	1,0	1019,8055	1023,0	0,9969
10	1024,0000	1024,0	1,0	2043,8055	2047,0	0,9984
11	2048,0000	2048,0	1,0	4091,8055	4095,0	0,9992
12	4096,0000	4096,0	1,0	8187,8055	8191,0	0,9996
13	8192,0000	8192,0	1,0	16379,8055	16383,0	0,9998
14	16384,0000	16384,0	1,0	32763,8055	32767,0	0,9999
15	32768,0000	32768,0	1,0	65531,8055	65535,0	1,0

We shall illustrate the comparison of these data with practical "know-how" of copper on Zhezkazgan and Balkhash mining-metallurgical combines (tab. 1) graphically in coordinates on figure 1 and on CODELCO mining-metallurgical combines (tab. 2) on figure 2. The factor of their correlation has made for , figure1, for , on figure 2 testifies the adequacy of suggested model of an information estimation of quality of products in consecutive operations of the technological circuit.

The size in this case does not influence the solution of a problem as it is reduced at calculation of level determinations 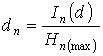and system determination .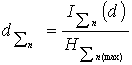

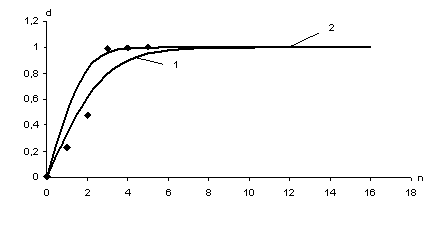
1 - dependence on new model , 2 - dependence on new model ,

points - experimental data

Figure 1 - Dependence of a degree of determination on a level on Zhezkazgan and Balkhash mining-metallurgical combines

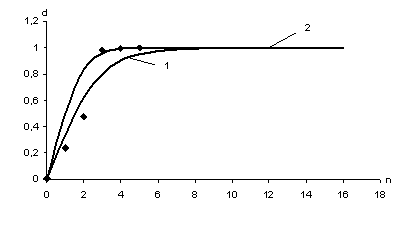
1 - dependence on new model , 2 - dependence on new model ,

points - experimental data

Figure 2 - Dependence of a degree of determination on a level on CODELCO mining-metallurgical combines

Influence of length of a code that is elements of system (target component and the basic impurity) can be revealed in the further researches. As a whole the improvement of quality of a product in process of its technological processing correlates with dynamics of growth of the determined component in abstract hierarchical system that proves the expediency of the further entropy-information analysis of similar systems. It can interest a reader as from the point of view of its theoretical analysis of various technological circuits, and also with its concern of the further development of entropy-information representations and display of any objects.

The literature

1. Кажикенова С. Ш. Информационная оценка качества технологических процессов производства свинца // Цветная металлургия. – 2009.-№.8. – С.22-29.

2 Kazhikenova S.Sh Information estimation on extraction and contents of technological redistribution аt steel production// Geomaterials. - Scientific Research Publishing, USA, 2012. – Vol.2№1. – Р.24-27.

3. Kazhikenova S.Sh New Technology for Refractory Material Preparation // Refractories and Industrial Ceramics. – SpringerLink, 2014. - Vol.55, № 2. – P. 108-111