Математика/5. Математичне моделювання
Юнак О.М., Пелещак Б.М., Охремчук
Н.Л., Метлевич Я.Р.
Львівський коледж Державного
університету телекомунікацій, Україна
Перетворення
зображення фрактальної структури типу “Фрактальний пил” (Множина Кантора) в рандомізовану
систему ітераційних функцій
У статті
розглядається результати розробки алгоритму формування рандомізованої системи
ітераційних функцій (РСІФ) з існуючого фрактального зображення типу “Фрактальний
пил” (Множина Кантора). Виведено
математичні формули та закономірності для розрахунку коефіцієнтів РСІФ.
Ключові слова: фрактал, множина Кантора, рандомізована
система ітераційних функцій (РСІФ).
Вступ. Побудова фракталів за допомогою системи
ітераційних функцій (СІФ) включає в себе два підходи: детермінований і
рандомізований. Детермінована система
ітераційних функцій (ДСІФ) дозволяє отримати зображення, але потребує
обробки великих масивів нулів та одиниць. В рандомізованому алгоритмі немає
необхідності зберігати великі масиви даних в пам’яті. Тому цим алгоритмом
зручно користовуватися на комп’ютерах з обмеженими ресурсами, обчислюючи одну
точку на кожному кроці і зразу відображаючи її на екран [1, с. 102-103]. Перевагою РСІФ над ДСІФ є також те, що
початкова множина складає всього одну точку. Формування РСІФ для побудови
фрактальних зображень є досить складним процесом. Тому в даній статті ми
запропонуємо новий підхід для формування РСІФ структур множин Кантора [2, c.
68-71].
Виклад основного матеріалу. Сформуємо РСІФ множини Кантора
(метод систем ітераційних функцій Барнслі [3, c. 66-67]), для цього задаємо координатну пряму ОХ виберемо дві точки А і В з координатами ха і хв,
та точку С з кординатою х, координата якої буде змінюватись на
половину відстані в сторону тієї точки, яка випаде (рандомізований алгоритм
вибору точка А чи В):
![]() хn = ха –
(ха –хn-1)/k
хn = ха –
(ха –хn-1)/k
хn = хв – (хв
–хn-1)/k (1)
де хn-1
– початкова координата точки С;
хn
– наступна координата точки С;
ха, хв – коодинати точок А і В;
k –
коефіціент пропорційності (відношення довжини відрізка до довжини відрізка
першої ітерації).
k = L/
ΔL1 (2)
де L - загальна довжина проміжку;
ΔL1 - довжина
відрізка першої ітерації.
Побудуємо фрактал “Множина Кантора” з коефіцієнту
пропорційності k=3 (L/ΔL1=3) для цього
застосуємо програмне забезпечення PascalABC.NET [4], та наберемо наступний код:
program Fractal;
uses GraphABC;
// Підключення модуля роботи з графікою
var
m,i,k:integer;
y,x:integer;
begin
k:=3;
// коефіціент подібності
y:=100; // початкова координата по у (вона не змінюється)
x:=100; //
початкова координата по х
for i:=1
to 100000 do // цикл
рисування точок
begin
m:=Random(2)+1;
//
рандомізована функція
if m=1
then
begin
x:=100-Round((100-x)/
k); // Round – функція заокруглення до
end; //
цілого значення
if m=2
then
begin
x:=1000-Round((1300-x)/ k);
end;
SetPixel(x,y,clred); //
рисування точки на екрані.
end;
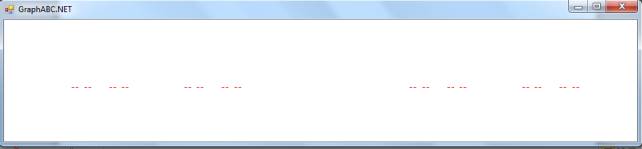
Результат програми k=3:
Для
різних коефіціентів k:

Для
коефіціента k=2 отримаємо:
![]()
Проведемо математичний аналіз методом комп’ютерного моделювання:
- якщо випадатиме цифра 1, то точку що з’явиться будемо позначати червоним кольором, якщо цифра
2 – синім:

-
поставимо
третю точку посередині відрізка та
виберемо коефіцієнт подібності k=4:
![]()
-
змінимо
розташування (координату) середньої точки відрізка:
![]()
Провівши
ряд математичних обчислень, можна сказати:
1) що
точка яка вибирається за допомогою рандомізованого алгоритму утворює свій
відрізок першої ітерації фрактала;
2) довжина
відрізка першої ітерації не залежить від місця розташування точки ΔL1=L/K.
Виходячи з
цих двох результатів, можна зробити висновок, що існує зв'язок між координатою
точки, яка вибирається за допомогою рандомізованого алгоритму та координатою
середини відрізка першої ітерації, яку вона утворює.
Виведемо
цю залежність:
Візьмемо
відрізок лежить на координатній прямій Ох довжиною L, початок котрого
знаходиться в точці 0. Відрізок ХпХк – відрізок першої ітерації, який
утворюється точкою з координатою Х2. Х1 – координата середини відрізка ХпХк.
L/k – довжина відрізка ХпХк.
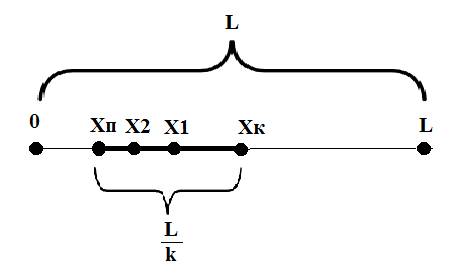
З даного
рисунку виводимо наступні закономірності:
Хк – Хп = L/k
(3)
Х1 – Хп = L/2k
=> Хп = Х1 – L/2k (4)
Хк – Х1 = L/2k => Хк
= Х1 + L/2k (5)
Так як точка Х2 повинна зберігати
пропорційність відносно відрізка 0L та відрізка ХпХк, випливає наступна
закономірність:
(Х2-Хп)/Х2 = (Хк-Х2)/(L-Х2) (6)
LХ2 – Х22 – LХп + ХпХ2 = Х2Хк –
Х22
LХ2 + ХпХ2 – Х2Хк = LХп
Х2(L – (Хк - Хп)) = LХп
(7)
Підставляємо
(3) і (4) в (7) та отримуємо:
Х2(L – L/k) = L(Х1 – L/2k)
Отримуємо залежність між координатою точки яка вибирається за допомогою рандомізованого
алгоритму Х2 та координатою
середини відрізка першої ітерації Х1:
Х2 = (kХ1 – L/2)/(k – 1) (8)
ПРАКТИЧНЕ ЗАСТОСУВАННЯ
В даному пункті за допомогою формули (8)
ми опишемо алгоритм написання РСІФ
для побудови фрактвлів, та виведення РСІФ з готових фракталів.
Спробуємо на прикладі перетворити
побудований фрактал в систему функцій, за допомогою яких можна потім буде його
відтворити

Крок 1. Помістити фігури першої ітерації в рівні прямокутники (по Х і по У
відповідно будуть свої коефіцієнти k):
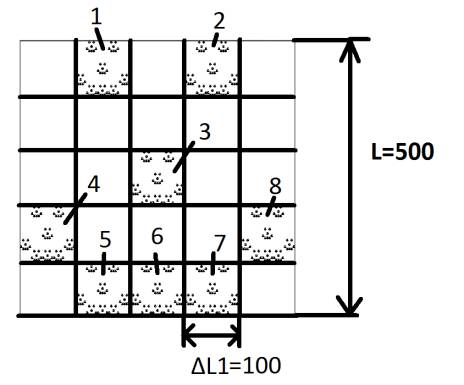
Крок 2. Знаходимо k згідно формули (2)
k= L/ΔL1 =500/100=5 .
Крок 3. Знаходимо координати точок середин
фігур Х1
Крок 4. За допомогою формули (8)
розраховуємо відповідні їм координати точки які вибирається за допомогою
рандомізованого алгоритму Х2.
Крок 5. Записуємо РСІФ згідно формул (1).
Крок 6. Програмування РСІФ.
Результати кроків 3-5 винесені в таблицю:
|
Номер фігури першої ітерації |
координати точки середини фігури |
координати точки які вибирається
за допомогою рандомізованого алгоритму |
РСІФ |
|
1 |
(150;0) |
(125;0) |
х = 125 – (125 –х)/5 y=0-(0-y)/5 |
|
2 |
(350;0) |
(375;0) |
х = 375 – (375 – х)/5 y=0-(0-y)/5 |
|
3 |
(250;250) |
(250;250) |
х = 250 – (250 –х)/5 y=250-(250-y)/5 |
|
4 |
(50;350) |
(0;375) |
х = 0 – (0 –х)/5 y=375-(375-y)/5 |
|
5 |
(150;500) |
(125;500) |
х = 125 – (125 –х)/5 y=500-(500-y)/5 |
|
6 |
(250;500) |
(250;500) |
х = 250 – (250 –х)/5 y=500-(500-y)/5 |
|
7 |
(350;500) |
(375;500) |
х =375 – (375 –х)/5 y=500-(500-y)/5 |
|
8 |
(450;350) |
(500;375) |
х= 500 –(500 –х)/5 y=375-(375-y)/5 |
Аналогічний способом можна перетворити
зображення у фрактал:



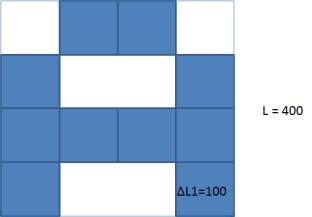
Висновок: Запропонований алгоритм та виведені
математичні формули допоможуть:
1. Спростити способи побудови
фрактальних структур, так як в основі алгоритму лежить система РСІФ, яка не потребує потужних
математичних обчислень;
2. Дозволить перетворювати
зображення у фрактал на базі РСІФ;
3. Відображати математичну модель
на основі РСІФ для існуючого фрактального зображення;
4. В сотні разів зменшить розмір
файлу фрактального зображення, так як не має необхідності зберігати координати
забраження всіх точок фракталу достатньо зберегти координати точок які
вибирається за допомогою рандомізованого алгоритму;
5. Даний алгоритм дозволяє
виконати пряму і зворотню задачу по побудові фрактальної структури. Тим самим
на базі цього алгоритму можна розробити автоматизовану систему для роботи з
відповідними фракталами.
Литература:
1. Ричард
М. Кроновер . Фракталы и хаос в динамических системах. Основы теории. Москва:
Постмаркет, 2000 – 352 с.
2. Е. Федер. Фрактали: Пер. с англ. – М.: Мир, 1991. –
254с.
3. Деменок
С. Л. Просто фрактал. – СПб.: ООО
«Страта», 2012. –
168 с.
4. Цветков А.С. Язык
программирования PASCAL, Система программирования ABC Pascal, Учебное пособие
для школьников 7-9 классов. Санкт-Петербург Павловск, 2015-2016 – 46с .