К.т.н. Земцова О.Г., д.т.н Шеин А.И.

Пензенский государственный университет архитектуры и строительства

Вычисление угловой скорости вращения опорной плоскости подвеса маятникового гасителя

Высотные сооружения башенного типа в значительной мере подвержены воздействию ветрового потока. При совпадении частоты ветрового воздействия с собственной частотой сооружения возможно возникновение резонанса, что повлечет за собой разрушение конструкций. Поэтому высотные сооружения оснащают гасителями колебаний. Одним из наиболее эффективных средств уменьшения амплитуд является маятниковый гаситель, представляющий собой массу, соединенную подвесом с защищаемым объектом [1].

Дифференциальные уравнения относительного движения гасителя можно записать в виде [2, 3]:

. (1)

Здесь индексы τ, e и k соответствуют относительному, переносному и кориолисову ускорениям.

При моделировании пространственного гасителя колебаний вектор ускорения Кориолиса можно записать в виде:

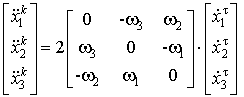. (2)

Так как сооружение в целом, и каждый ярус в отдельности, не являются абсолютно твердыми телами, при определении угловых характеристик плоскости маятникового подвеса будем использовать кинематические характеристики заранее выбранных узлов. Угловую скорость вращения опорной плоскости подвеса маятника вокруг вертикальной оси можно определить через скорости движения двух узловых точек яруса l и n (рис. 1). При этом углы, определяющие положение центра вращения плоскости маятникового подвеса, определим через направляющие косинусы:

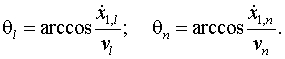(3)

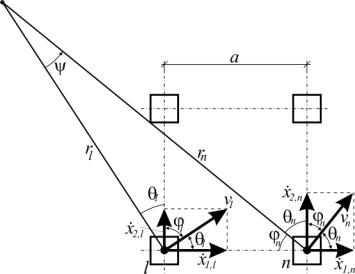
Рис. 1

С учетом принятых допущений и геометрических параметров угловая скорость вращения опорной плоскости маятникового подвеса вокруг вертикальной оси будет равна:

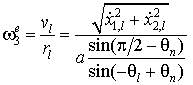. (4)

Таким образом, выведена расчетная формула для определения угловой скорости яруса башни, в центральной точке которого закреплен маятниковый гаситель колебаний. Полученная формула может быть использована в математическом моделировании гашения колебаний высотных сооружений [4] при дальнейших исследованиях.

Литература:

1. Шеин А.И., Земцова О.Г. Гашение колебаний высотных сооружений. Ч.2. Математическое моделирование объектов с гасителями при ветровой нагрузке. – Пенза: ПГУАС, 2012. – 132 с.

2. Земцова О.Г. Моделирование и исследование динамики высотных сооружений с гасителями колебаний: дис. … канд. техн. наук. Пенза, 2013. 152 с.

3. Шеин А.И., Земцова О.Г. Схемы и теория гасителей пространственных колебаний сооружений // Региональная архитектура и строительство. 2010. № 1. С. 45-52.

4. Шеин А.И. Математическое моделирование механических систем на примере задачи гашения колебаний высотных сооружений [Электронный ресурс] // Моделирование и механика конструкций. 2015. №1. URL: http://mechanics.pguas.ru/Plone/nomera-zhurnala/no1/matematicheskoe-modelirovanie-chislennye-metody-i-kompleksy-programm/matematicheskoe-modelirovanie-mehanicheskih-sistem-na-primere-zadachi-gasheniya-kolebanii-vysotnyh-sooruzhenii/at_download/file.