К.т.н. Бойко С.Н., Михайличенко Д.А., Блинова А.С., студентка

Кременчугский национальный университет им. М. Остроградского

ИССЛЕДОВАНИЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ ПРИ ПУСКЕ СИНХРОННОГО ДВИГАТЕЛЯ С ШИРОТНО-ИМПУЛЬСНЫМ ПРЕОБРАЗОВАТЕЛЕМ ЧАСТОТЫ

Введение. Пуск мощных синхронных электрических двигателей имеющих большие моменты инерции и предназначенных для функционирования в комплексе современных электромеханических систем, как правило, производится при помощи пусковых устройств, в т.ч. на основе полупроводниковых преобразователей электрической энергии [1, 2]. При этом алгоритмы формирования требуемых выходных электрических параметров таких пусковых устройств могут быть различными и варьироваться в силу требований технологи функционирования конкретного механизма [3, 4].

Оценка и выбор наиболее подходящего способа формирования выходных форм кривых тока и напряжения широтно-импульсного преобразователя (ШИП) при широтно-импульсной модуляции (ШИМ), для конкретной электротехнической системы, задача не однозначная, ввиду существования нескольких вариантов управления преобразователем. Поэтому актуальным является решение вопросов связанных с моделированием пуска синхронного электрического двигателя (СЭД) с ШИП частоты при различных законах формирования выходных параметров преобразователя [5,6].

Цель работы. Целью работы является анализ переходных процессов при пуске СЭД с использованием ШИП с синусоидальным, трапецеидальным и прямоугольным выходным напряжением на базе математической модели построенной в координатах ток статора и потокосцепление статора.

Материалы исследований. Наиболее часто переходные процессы в электромеханических системах с СД рассматриваются в координатных осях d, q.

Однако особенностью применения преобразований в координатных осях d, q является положение о чисто синусоидальном фазном напряжении на статорных обмотках СД. И использование формирователей реального напряжения на его обмотках при использовании ШИП в режиме реального времени может привести к неоправданным погрешностям при моделировании. Для исследования использована математическая модель СЭД в основу построения которой положена обобщенная система дифференциальных уравнений СЭД Парка – Горева в векторной форме записи [7]. Для реализации ШИМ управления ШИП использован алгоритм формирования пространственного вектора напряжения. При моделировании приняты параметры серийного СЭД ДС260/44-36УХЛ4. Решение поставленной задачи проводилось в программной среде Фортран.

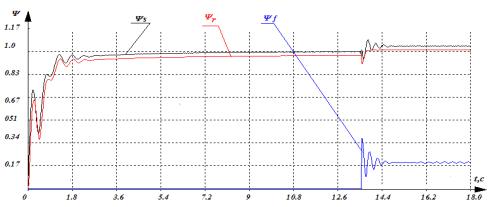
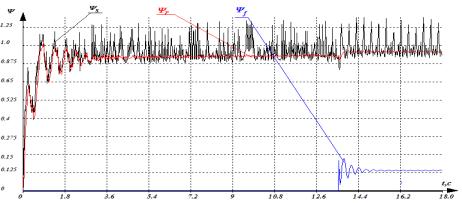
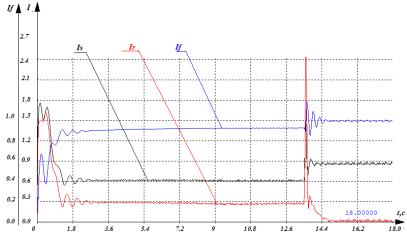
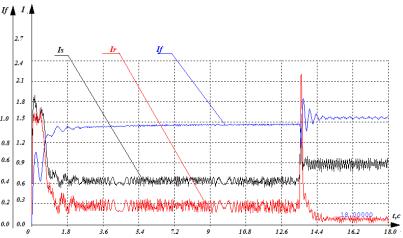
Результаты моделирования пуска СЭД при синусоидальном, трапецеидальном и прямоугольном напряжении питания приведены на рис.1 - рис.3 соответственно.

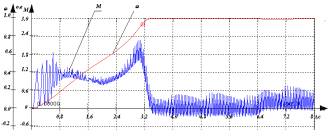
Среднее значение пускового момента (рис.1а) составляет 0,9-1,2 номинального. При этом время разгона составляет 3,2c. Токи синхронного двигателя, пульсирующие с модуляцией низкой частоты (рис.1б) с амплитудой 0,4-0,5 номинального тока, обуславливают пульсации момента величиной 0,3-0,4 номинального. Среднее значение пускового момента составляет 1,8 номинального, а время пуска приблизительно 2c (рис.2а).

а)

б)

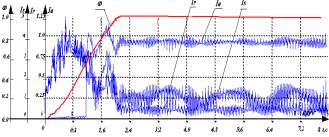
Рисунок 1 – Переходный процесс по скорости – ω и моменту – M при синусоидальном напряжении а); переходный процесс по скорости – ω, току статора – Is, пусковой обмотки – Ir и току возбуждения – Iв при синусоидальном напряжении б)

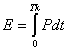а)

б)

Рисунок 2 – Переходный процесс по скорости – ω и моменту – M при трапецеидальном трехфазном напряжении а); переходный процесс по скорости – ω, току статора – Is, пусковой обмотки – Ir и току возбуждения – Iв при трапецеидальном напряжении б)

После включения возбуждения величина пульсаций модулируется низкими частотными колебаниями, обусловленными колебательными свойствами синхронного двигателя, которые составляют величину 0.6 номинального момента (рис.2б). Среднее значение пусковых токов статора и короткозамкнутой обмотки при разгоне в 3 раза превышают номинальные значения. Использование ШИП частоты без фильтрующих и регулирующих устройств, приводит к пульсациям статорных, следовательно, роторных токов и момента.

а)

б)

Рисунок 3 – Переходный процесс по скорости – ω и моменту – M при прямоугольном трехфазном напряжении а); переходный процесс по скорости – ω, току статора – Is, пусковой обмотки – Ir и току возбуждения – Iв при прямоугольном напряжении б)

Результаты моделирования пуска синхронного двигателя со ступенчатым трех фазным напряжением, приведены на рис. 3.

Характер переходных процессов при прямоугольном фазном напряжении схож с процессами при трапецеидальном фазном напряжении.

После включения возбуждения величина пульсаций модулируется низкими частотными колебаниями, обусловленными колебательными свойствами синхронного двигателя, составляет величину 0.7 номинального момента. При прямоугольном увеличении нагрузки в момент времени t = 6,4c амплитуда пульсаций увеличивается при сохранении частоты модуляции.

На рис. 4 приведены графики потокосцеплений ψ при разных законах модуляции фазного напряжения.

Мощность, потребляемая электромеханической системой для выбранной системы координат и системы дифференциальных уравнений, моделирующих переходные процессы, в общем случае можно определить по формуле:

,

где Р –мощность потребляемая синхронным двигателем, Т_к – время цикла [7].

а)

б)

в)

Рисунок 4 – Графики потокосцеплений ψ при разных законах модуляции фазного напряжения – синусоидальной модуляции (а), трапецеидальной модуляции (б), ступенчатой модуляции (в)

Результаты расчета переходных процессов по току статора, коротко-замкнутой пусковой обмотки и обмотки возбуждения приведены на рис. 5.

а)

б)

в)

Рисунок 5 – Переходные процессы по токам двигателя при синусоидальной модуляции (а), при трапецеидальной форме фазного напряжения (б), при ступенчатой форме фазного напряжения (в)

Выводы. Полученные результаты моделирования процесса пуска СЭД показывают, что наличие высокочастотных составляющих в токах двигателя при трапецеидальной и ступенчатой форме фазного напряжения создают дополнительные сложности при реализации сигналов обратных связей, так как при этом требуется наличие фильтров, повышающих порядок системы регулирования и снижающих быстродействие замкнутой системы.

Список использованной литературы:

1. Hioki Т., Jamamoto H., Mizuno S., Jnogushi H. Thyristor Starting System for Okayoshino Power Plant -Toshiba Review, 1979, № 122, jul-aug

2. Черный А.П., Гладарь А.И., Осадчук Ю.Г., Курбанов И.Р., Вошун А.Н. Пусковые системы нерегулируемых электроприводов: Монография – Кременчуг: ЧП Щербатых А.В., 2006. – 280с.

3. Синчук И.О. Полупроводниковые преобразователи электрической энергии в структурах электроприводов. Схемотехника и принципы управления / Синчук И.О., Чернышев А.А., Киба И.И., Пасько О.В., Ключка О.Е., Мельник О.Е./ Учебное пособие. Под редакцией проф. Синчука О.Н. – Кременчуг, Вид. Щербатих О.В., 2008. – 88с.

4. Tihanyi, L. EMC in Power Electronics / L. Tihanyi. – N.Y.: IEEE Press, 1995. – 402 p

5. Вейнгер А.М. Регулируемый синхронный электропривод. – М.: Энергоатомиздат, 1985. – 224с., ил.

6. Рудаков В.В.и др. Асинхронные электроприводы с векторным управлением/В.В.Рудаков, И.М. Столяров, В.А . Дартау. – Л.: Энергоатомиздат, Ленингр. отд-ние, 1987. – 136с.: ил.

7. Ключев В.И. Теория электропривода: Учебник для вузов. – М.: Энергоатомиздат, 1985. – 560с., ил.