Технические науки/5. Энергетика

Панюкова Д.В., д.т.н. Нурпеисова Г.Б., к.т.н. Нурпеисова Т.Б.

Казахская Автомобильно-Дорожная академия им. Л.Б. Гончарова, Казахстан

Разработка нейронных моделей краткосрочного прогнозирования энергопотребления

В процессе оперативного управления энергосистемами непрерывно решается задача экономичного распределения нагрузок между генераторами электростанций, чтобы с минимальными затратами компенсировать генерируемой мощностью текущие изменения электропотребления без снижения уровня надежности системы. Для надежного и экономичного распределения нагрузки между электростанциями требуются краткосрочные прогнозы потребления в основных узлах энергосистемы.

Рассмотрим использование в прогнозировании электропотребления нейронных сетей, для обучения которых будут использованы данные по разным промышленным регионам Российской Федерации. Обучающая выборка представляет собой почасовые данные электропотребления за все рабочие дни декабря 2004 года, января и февраля 2005 года. Данные электропотребления за зимний период 2004-2005 года были размещены на сайте некоммерческого партнерства «Совет рынка по организации эффективной системы оптовой и розничной торговли электрической энергией и мощностью» (www.np-ats.ru). С использованием этих обучающих выборок была оценена эффективность различных моделей прогнозирования.

Модель прогнозирования на основе многослойной нейронной сети прямого распространения была создана с помощью функции вида

net=newff(PR, [S1 S2 Sn], {TF1 TF2 TFn}, BTF, BLF, PF),

где PR – матрица минимальных и максимальных значений входных элементов, Si – размер i-го скрытого слоя, TFi – функция активации нейронов i-го слоя, BTF – функция обучения сети, по умолчанию traingd (классический алгоритм обратного распространения ошибки), BLF – функция настройки весов и смещений, по умолчанию learngdm (функция коррекции весов и смещений, реализующая градиентный метод оптимизации с инерционной составляющей), PF – функция ошибки, по умолчанию mse (среднеквадратичная ошибка) [1].

Обучение сети производится с помощью функции

net1 = train(net, P, T),

где net1 – имя сети, net – имя созданной сети, P и T – входная и выходная матрицы обучающей выборки соответственно.

Тестирование сети производится с помощью функции

Xout_prov_net=sim(net1,Xin),

где Xout_prov_net – имя вектора, куда заносится результат тестирования, net1 – имя тестируемой сети, Xin – входные данные для тестирования.

Функция

gensim(net1)

создает S-модель сети.

На рисунке 1 представлен график фактического электропотребления и электропотребления, полученного с помощью сети. По нему можно оценить точность обучения. На рисунке 2 представлен график фактического и прогнозного электропотребления.

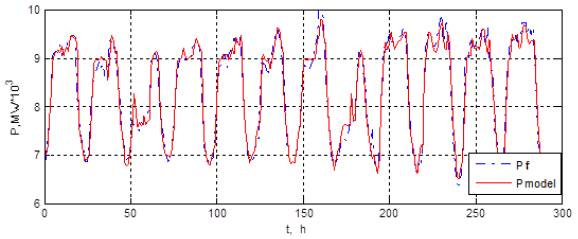
Рисунок 1. Расчетное и фактическое электропотребление системы

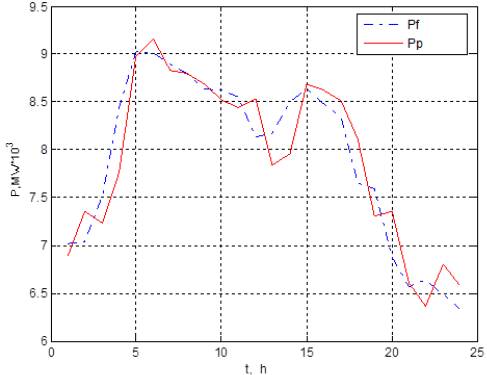
Рисунок 2. Прогнозное и фактическое электропотребление системы

С помощью данной нейронной сети получены следующие результаты: ошибка обучения сети 2.97%; ошибка прогноза 3.01%.

Модель прогнозирования на основе радиальной базисной сети (RBF-сети) была создана с помощью функции вида

net=newrb(P, T, goal, spread),

где P – матрица входных векторов, T –матрица целевых векторов, spread – отклонение (по умолчанию 1), goal – заданная среднеквадратичная ошибка [1].

Результаты прогнозирования с использованием RBF-сети: ошибка обучения 1,58%; ошибка прогноза 2,18%.

Такая точность прогноза является очень высокой. Графики фактического и спрогнозированного с помощью такой сети электропотребления приведены на рисунке 3.

Так, для сравнения, предварительно рассмотренные регрессионные модели характеризуются приблизительно одинаковой точностью прогнозирования около 2,8% (прогноз на один час вперед).

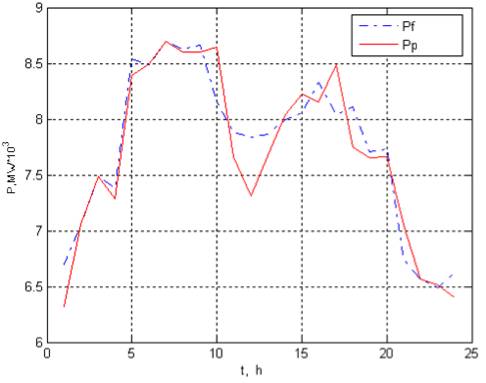
Рисунок 3. Фактическое и прогнозируемое электропотребление

Точность прогноза с помощью радиальной базисной сети весьма высока, однако структура сети такова, что из-за большого объема обучающей выборки сеть образует огромное количество нейронов на скрытом слое и связей. В итоге время обучения становится слишком большим и требует значительных ресурсов памяти компьютера.

Таким образом, если необходима высокая точность прогноза, а время обучения сети не критично, лучше использовать радиальную базисную сеть. Она обеспечит прогноз с ошибкой всего лишь около 2%.

Если же прогнозную модель необходимо получить, используя меньше вычислительных ресурсов, достаточно воспользоваться регрессионными моделями прогнозирования. Такие модели в короткое время обеспечат прогноз со средним значением ошибки менее 3%.

Литература:

1. Дьяконов В., Круглов В. Математические пакеты расширения MATLAB. Специальный справочник. - СПб.: Питер, 2001. – 480с.