Технические науки/2 Механика

К.т.н. Романюк А. Д., к.т.н. Мамаев Л.М., к.т.н. Кабаков А.М.,

к.т.н. Телипко Л.П.

Днепродзержинский государственный технический университет

ОПТИМИЗАЦИЯ ПЕРЕДАТОЧНОЙ ФУНКЦИИ МЕХАНИЗМА

В процессе установившегося режима работы механизма кинематические характеристики его звеньев являются периодическими функциями. Причиной периодических колебаний скорости звеньев та кинематических пар является периодический характер изменения действующих сил и передаточной функции механизма привода. Уменьшения амплитуды колебания скорости звена приведения обычно добиваются увеличением приведенного момента инерции. Такой подход приводит к увеличению инерционности механизма в следствии установлении на валу звена приведения дополнительной массы, которую называют маховиком. Увеличение приведенного момента инерции механизма ухудшает его динамические характеристики, приводит к увеличению времени разгона и снижению производительности машинного агрегата. Введение дополнительных масс увеличивает вес машинного агрегата, что не рационально для широкого класса современных машин, особенно транспортных [1,2,3].

Значительное влияние на закон движения звена приведения может оказать периодически меняющаяся составляющая приведенного момента инерции механизма. Если характер изменения внешних сил, действующий на звенья механизма, изменить практически невозможно, то при проектировании машинного агрегата можно обеспечить оптимальный характер изменения его приведенного момента инерции, чтобы уменьшить изменения скорости выбранного звена приведения. Характер изменения приведенного момента инерции за время установившегося движения может быть выбран таким, чтобы соответствовать изменениям суммарной работы. Если изменения кинетической энергии механизма за счет приведенного момента инерции равны изменениям суммарной работы

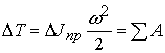, (1)

то выбранная скорость движения звена приведения будет постоянной. Изменение приведенного момента инерции механизма связана с его кинематической передаточной функцией . Таким образом, задача синтеза передаточного механизма, оптимального по точности движения исполнительного органа в установившемся режиме работы, может быть сформулирована как определение его кинематической передаточной функции, обеспечивающей минимальные колебания скорости движения звена приведения.

Основой расчета оптимальной передаточной функции механизма машинного агрегата служит дифференциальное уравнение движения звена приведения, за которое принят вал исполнительного механизма [4], соединенный с передаточным механизмом:

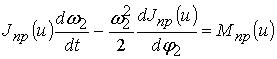, (2)

где: – приведенный момент инерции; – искомая передаточная функция механизма; – суммарный приведенный момент, зависящий от передаточной функции механизма и координат положения звеньев; ₂ – угловая скорость вала исполнительного механизма; – угловая координата исполнительного органа.

Поскольку приведенный момент инерции однозначно определяется передаточной функцией механизма, зависящей от угловой координаты исполнительного органа , то

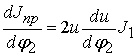. (3)

Подставляя уравнения (3) в дифференциальное уравнение движения звена приведения (2) с учетом, что:

; ; ,

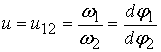где ₁ – угловая скорость вала двигателя; – момент двигателя, не зависящий от углового вращения вала; – момент исполнительного механизма, зависящий от угловой координаты исполнительного органа, получим следующую зависимость

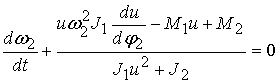. (4)

Решением дифференциального уравнения (4) может быть закон движения при заданной передаточной функции механизма . Можно решать обратную задачу определения оптимальной функции механизма , обеспечивающей воспроизведение заданного закона движения звена приведения .

Так как, в основном движение вала исполнительного механизма происходит с постоянной скоростью , то уравнение (4) принимает вид

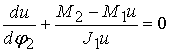(5)

Решение нелинейного дифференциального уравнения (5) представляет определенные трудности из-за того, что момент двигателя в установившемся режиме не является независимой переменной, а связан с моментом, действующим на исполнительный механизм , и может быть определен из условия равенства работ сил движущих и сопротивления за полный цикл движения :

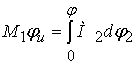. (6)

Разделяя переменные дифференциального уравнения (5) и учитывая, что

,

получим после его интегрирования

,

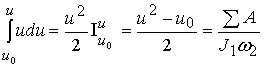где – искомое текущее значение оптимальной передаточной функции; 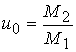– начальное значение передаточной функции, полученное из условия в начальный момент.

Полученный результат представляет расчетное выражение для определения оптимального характера изменения передаточной функции

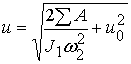. (7)

Полученное уравнение (7) к сожалению, не дает точного расчета величины оптимальной передаточной функции, так как работа движущих сил и – не только функция координат звена приведения , но и искомой передаточной функции.

Таким образом, точное решение уравнения возможно только с помощью применения метода последовательного приближения.

Полученный, с помощью расчета, оптимальный характер изменения передаточной функции механизма обеспечивает нулевую степень неравномерности вращения звена приведения только на одном выбранном скоростном режиме. Такое решение возможно только вследствие увеличения степени неравномерности движения других звеньев.

Рассмотренный метод позволяет исключить применение маховика, так как эффект проявляется независимо от момента инерции исполнительного механизма.

Литература.

1. Геминтерн В.Н., Коган Б.М. Методы оптимального проектирования. – Энергия, – 1980.

2. Соболь И.М., Статников Р.Б. Выбор оптимальных параметров в задачах со многими критериями. – М.: Наука, – 1981.

3. Динамический синтез передаточного механизма машинного агрегата / Леонов И. В. // Известие вузов. Машиностроение.: №7, 1981. – С.39 – 42.

4. Определение оптимальной по быстродействию передаточной функции механизма / Романюк А.Д. // Сборник научных трудов Керченского государственного морского технологического университета «Механизация производственных процессов рыбного хозяйства, промышленных и аграрных предприятий». Выпуск 9. – Керчь.: КГМТУ, 2008. – С. 70 – 74.