Технические науки / 6

Технические науки / 6.Электротехника и радиоэлектроника.

к.т.н. Черных А.Г., Жуков П.А., Загрединов С.С.

Иркутский государственный аграрный университет, Россия

РАСЧЕТ ЦЕПЕЙ СИНУСОИДАЛЬНОГО ТОКА С СОСРЕДОТОЧЕННЫМИ ПАРАМЕТРАМИ С ИСПОЛЬЗОВАНИЕМ ПРОГРАММНОЙ СРЕДЫ MATLAB-SIMULINK НА ПРИМЕРЕ .M ФАЙЛА

Для преподавания такой дисциплины как ТОЭ требуется универсальная программа моделирования всевозможных процессов в цепях с сосредоточенными параметрами, имеющая большую элементную базу и простоту построения моделей. Программа моделирования должна обеспечивать проведение лабораторных и практических работ по вышеуказанной дисциплине с возможностью отображения результатов моделирования тех или иных процессов в реальном времени. Пакет программ MatLab, адаптированных под операционную систему Windows, – в полной мере соответствует поставленной задаче.

Однако, работа в режиме калькулятора в среде MatLAB, несмотря на довольно значительные возможности, во многих отношениях неудобна. Невозможно повторить предшествующие вычисления и действия при новых значениях исходных данных без повторного набора предшествующих операторов. Нельзя возвратиться назад и повторить некоторые действия, или по некоторому условию перейти к выполнению другой последовательности операторов. И вообще, если количество операторов значительно, становится проблемой отладить правильную их работу из-за неминуемых ошибок при наборе команд. Поэтому сложные, с прерываниями, сложными переходами по определенным условиям, с часто повторяемыми однотипными действиями вычисления, которые, вдобавок, необходимо проводить неоднократно при измененных исходных данных, требуют их специального оформления в виде записанных на диске файлов, т. е. в виде программ. Преимущество программ в том, что, так как они зафиксированы в виде записанных файлов, становится возможным многократное обращение к одним и тем же операторам и к программе в целом. Это позволяет упростить процесс отладки программы, сделать процесс вычислений более наглядным и прозрачным, а благодаря этому резко уменьшить возможность появления ошибок при разработке программ. Кроме того, в программах возникает возможность автоматизировать также и процесс изменения значений первоначальных параметров в диалоговом режиме.

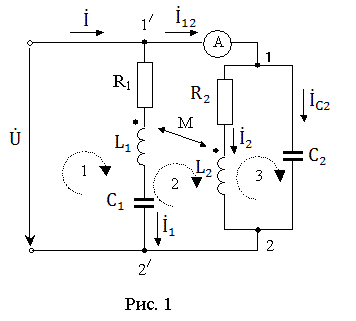
В качестве примера рассмотрим следующую задачу: Для схемы (см. рис. 1) определить токи в ветвях схемы, коэффициенты мощности cos j, полную S, активную Р и реактивную Q мощности ветвей и всей электрической цепи переменного тока.

Процедура решения рассматриваемой задачи в системе MatLab с использованием соответствующего m. файла имеет вид:

>> syms R1 R2 L1 L2 C1 C2 a b real

>> dI1 = sym('diff(I1(t),t)');

>> dI2 = sym('diff(I2(t),t)');

>> dQ1 = sym('diff(Q1(t),t)');

>> dQ2 = sym('diff(Q2(t),t)');

>> I1 = sym('I1(t)');

>> I2 = sym('I2(t)');

>> Q1 = sym('Q1(t)');

>> Q2 = sym('Q2(t)');

>>syms t s

E = a*sin(b*t);

>> eq1 = dI1+I1*R1/L1+Q1/(C1*L1)-E/L1;

>> eq2 = dI2+I2*R2/L2-E/L2;

>> eq3 = dQ1-I1;

>> eq4 = dQ2-a*b*C2*cos(b*t);

>> L11 = laplace(eq1,t,s)

L11 = s*laplace(I1(t), t, s) - I1(0) + (R1*laplace(I1(t), t, s))/L1 + laplace(Q1(t), t, s)/(C1*L1) - (a*b)/(L1*(b^2 + s^2))

>> L22 = laplace(eq2,t,s)

L22 = s*laplace(I2(t), t, s) - I2(0) + (R2*laplace(I2(t), t, s))/L2 - (a*b)/(L2*(b^2 + s^2))

>> L33 = laplace(eq3,t,s)

L33 = s*laplace(Q1(t), t, s) - Q1(0) - laplace(I1(t), t, s)

>> L44 = laplace(eq4,t,s)

L44 = s*laplace(Q2(t), t, s) - Q2(0) - (C2*a*b*s)/(b^2 + s^2)

>> syms LI1 LI2 LQ1 LQ2

NI1=subs(L11,{R1,R2,L1,L2,C1,C2,a,b,'I1(0)','I2(0)','Q1(0)'},{5,10,20/314,10/314,1/1570,1/6280,120,314,0,0,0})

NI1 = s*laplace(I1(t), t, s) - 591576/(s^2 + 98596) + 24649*laplace(Q1(t), t, s) + (157*laplace(I1(t), t, s))/2

>> NI2 =

subs(L22,{R1,R2,L1,L2,C1,C2,a,b,'I1(0)','I2(0)','Q1(0)'},{5,10,20/314,10/314,1/1570,1/6280,120,314,0,0,0})

NI2 = s*laplace(I2(t), t, s) - 1183152/(s^2 + 98596) + 314*laplace(I2(t), t, s)

>> NQ1 =

subs(L33,{R1,R2,L1,L2,C1,C2,a,b,'I1(0)','I2(0)','Q1(0)'},{5,10,20/314,10/314,1/1570,1/6280,120,314,0,0,0})

NQ1 = s*laplace(Q1(t), t, s) - laplace(I1(t), t, s)

>> NQ2 =

NQ2 = subs(L44,{C2,a,b,'Q2(0)'},{1/6280,120,314,0})

NQ2 = s*laplace(Q2(t), t, s) - (6*s)/(s^2 + 98596)

>> NI1 =...

subs(NI1,{'laplace(I1(t),t,s)','laplace(I2(t),t,s)','laplace(Q1(t),t,s)','laplace (Q2(t),t,s)'},{LI1,LI2,LQ1,LQ2})

NI1 = (157*LI1)/2 + 24649*LQ1 + LI1*s - 591576/(s^2 + 98596)

>> NI1 = collect(NI1,LI1)

NI1 = (s + 157/2)*LI1 + 24649*LQ1 - 591576/(s^2 + 98596)

>> NI2 =...

subs(NI2,{'laplace(I1(t),t,s)','laplace(I2(t),t,s)','laplace(Q1(t),t,s)','laplace (Q2(t),t,s)'},{LI1,LI2,LQ1,LQ2})

NI2 = 314*LI2 + LI2*s - 1183152/(s^2 + 98596)

>> NI2 = collect(NI2,LI2)

NI2 = (s + 314)*LI2 - 1183152/(s^2 + 98596)

>> NQ1 =...

subs(NQ1,{'laplace(I1(t),t,s)','laplace(I2(t),t,s)','laplace(Q1(t),t,s)','laplace (Q2(t),t,s)'},{LI1,LI2,LQ1,LQ2})

NQ1 = LQ1*s - LI1

>> NQ1 = collect(NQ1,LQ1)

NQ1 = s*LQ1 - LI1

>> NQ2 =...

subs(NQ2,{'laplace(I1(t),t,s)','laplace(I2(t),t,s)','laplace(Q1(t),t,s)','laplace (Q2(t),t,s)'},{LI1,LI2,LQ1,LQ2})

NQ2 = LQ2*s - (6*s)/(s^2 + 98596)

>> NQ2 = collect(NQ2,LQ2)

NQ2 = s*LQ2 - (6*s)/(s^2 + 98596)

>> [LI1, LI2, LQ1, LQ2] = solve(NI1, NI2, NQ1, NQ2, LI1, LI2, LQ1, LQ2)

LI1 = (1183152*s)/((s^2 + 98596)*(2*s^2 + 157*s + 49298))

LI2 = 1183152/((s^2 + 98596)*(s + 314))

LQ1 =1183152/((s^2 + 98596)*(2*s^2 + 157*s + 49298))

LQ2 = 6/(s^2 + 98596)

>> I1 = ilaplace(LI1, s, t)

I1 = (12*sin(314*t))/5 - (36*cos(314*t))/5 + (36*(cos((157*15^(1/2)*t)/4) –

(15^(1/2)*sin((157*15^(1/2)*t)/4))/9))/(5*exp((157*t)/4))

>> I2 = ilaplace(LI2, s, t)

I2 = 6/exp(314*t) - 6*cos(314*t) + 6*sin(314*t)

>> Q1 = ilaplace(LQ1, s, t)

Q1 = (6*(cos((157*15^(1/2)*t)/4) + (5*15^(1/2)*sin((157*15^(1/2)*t)/4))/3))/

(785*exp((157*t)/4)) – (18*sin(314*t))/785 - (6*cos(314*t))/785

>> Q2 = ilaplace(LQ2, s, t)

Q2 = (3*sin(314*t))/157

>> IC2=diff(Q2,t)

IC2 = 6*cos(314*t)

>> I1 = @(t) (12*sin(314*t))/5 - (36*cos(314*t))/5 +

(36*(cos((157*15^(1/2)*t)/4) –

(15^(1/2)*sin((157*15^(1/2)*t)/4))/9))/(5*exp((157*t)/4));

>> I2 = @(t) 6/exp(t*314) - 6*cos(t*314) + 6*sin(t*314);

>> IC2 = @(t) 6*cos(314*t);

>> I = @(t) (12*sin(314*t))/5 - (36*cos(314*t))/5 +

(36*(cos((157*15^(1/2)*t)/4) - (15^(1/2)*sin((157*15^(1/2)*t)/4))/9))/

(5*exp((157*t)/4))+6/exp(t.*314) – 6*cos(t.*314) + 6*sin(t.*314)+6*cos(314*t);

>> subplot(2,2,1); ezplot(I1,[0 0.08]);

title('Current'); ylabel('I1(t)'); grid

subplot(2,2,2); ezplot(I2,[0 0.08]);

title('Current'); ylabel('I2(t)'); grid

subplot(2,2,3); ezplot(IC2,[0 0.08]);

title('Current'); ylabel('IC2(t)'); grid

subplot(2,2,4); ezplot(I,[0 0.08]);

title('Current'); ylabel('I(t)'); grid

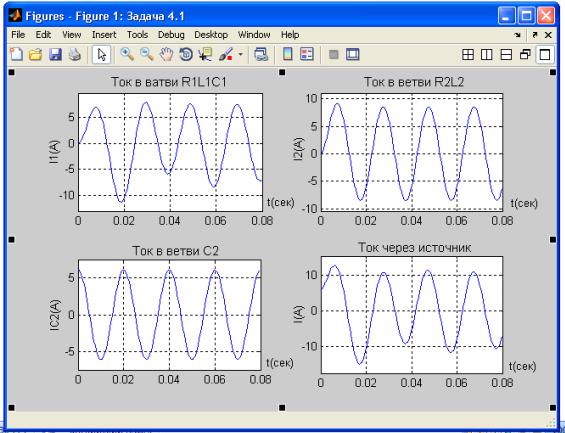
Вывод: представленный выше материал способствует приобретению студентами практических навыков при проведении компьютерных расчетов в программной среде Matlab-Simulink с использованием виртуальных пакетов Simulink и Power System Blockset на примере расчетной цепи однофазного синусоидального тока с использованием .m файла

Литература:

1. Общая электротехника / Под ред. А.Т. Блажкина. – Л.: Энергоатомиздат. 1986. – 592 с.

2. Общая электротехника Ю.М. Борисов и др. – М.: Энегоатомиздат. 1985.

3. Электротехника: практикум / Учебное пособие // А.Г. Черных – Иркутск: ИрГСХА , 2009. – 202 с.