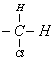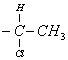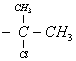УДК 541(636+42)

ПРОСТРАНСТВЕННАЯ ДОСТУПНОСТЬ РЕАКЦИОННОГО ЦЕНТРА

Ж. Е. Егинбаев кандидат химических наук,

доцент КазНТУ имени К.И.Сатпаева, г.Алматы, Казахстан

Пространственное экранирование реакционного центра (РЦ) молекулы различными структурными элементами ее значительной мере наряду с электронным фактором определяет скорость процесса [1].

В этой работе предлагается методика расчета пространственных препятствий (ПП) и практическое использование её на конкретных примерах.

В основу расчета ПП положена взаимосвязь между степенью экранирования РЦ и закрытой для атакующего реагента частью телесного направления. Так, для атаки изолированного атома реагентами открыто полное телесное направление (4p стерадиан) в случае же молекулы доступ к РЦ уменьшается.

Методика расчета ПП была разработана и проиллюстрирована на примере метилакрилата (МА) в трех конформациях (рисунок 1). Реакционным центром был выбран b–углеродный атом (С₃), который по данным квантово-химического расчета и эксперимента является наиболее активным в радикальной полимеризации. С целью учета особенностей взаимного расположения атомов в пространстве определены координаты атомов по известной геометрии данной молекулы в произвольной системе координат.

Размеры электронного облака были оценены по длинам соответствующих связей. Так среднее расстояние внешних валентных электронов от ядер атомов С₃ и С₄ (имеющих одинаковую гибридизацию), которые приближенно принято за линейный размер электронного облака, предположили равным половине С₃–С₄ (). Размер электронных облаков других атомов будет определяться между длиной соответствующей связи и радиусом электронного облака соседнего с ним атома r_i: = .

На рисунке 1а, б и в показаны сечения (заштрихованные участки) трехмерных фигур метилакрилата, изображающих форму электронных облаков, на соответствующих связях.

Часть полного телесного направления, заслоненная соседним с РЦ i–атомом (например, атомом 1 на рисунке 1), вычисляется по формуле (1), где W – символ, характеризующий величину ПП, выраженных в единицах полного телесного угла (4p стерадиан), L_i=суть образующие соответствующих конусов, а – их высоты.

Для вычисления части полного телесного направления, закрытой фигурой

(рисунок 1а), следует предварительно соединить РЦ (С₃) с её вершинами.

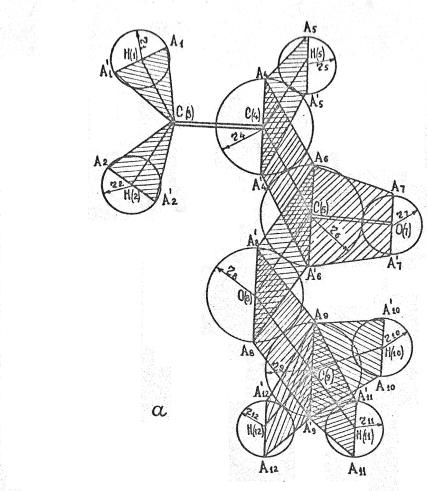
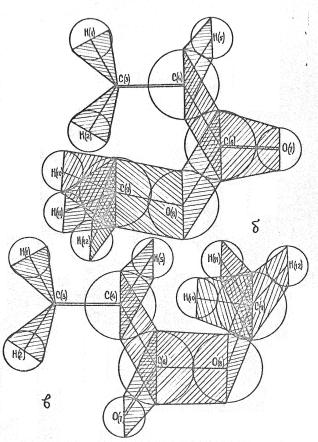
Рисунок 1. Сечения электронных облаков на связях в молекулах МА

Выбрав три точки, лежащие на основании полученной при этом пирамиды, можно составить уравнение плоскости её основания. Тогда высота пирамиды находится по известной формуле как расстояние от заданной точки (РЦ) до плоскости. Площадь основания пирамиды определяется непосредственной квадратурой с учетом его (основание) наклона к какой-либо координатной плоскости. Далее, т. к. часть телесного направления, закрытую основанием пирамиды, нельзя непосредственно выразить в стерадианах, заменим эту пирамиду равновеликим ей конусом. Приняв за высоту конуса отрезок, соединяющий РЦ с серединой длины соответствующей связи, лежащей на основании рассматриваемой пирамиды, определяем радиус основания конуса, поле чего не представляет трудности нахождение длины его образующей. Такое приближение позволяет вычислить часть телесного направления, закрытую заштрихованными трапециями (рисунок 1) по формуле (1).

Таким образом, для j конформации суммарная закрытая часть полного телесного направления относительно РЦ вычисляется согласно соотношению:

,

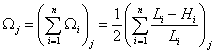где п – число фигур, эффективно заслоняющих РЦ от атаки реагентов.

Из рисунка 1 видно, что одинаковые структурные элементы при различной конформации по разному экранируют РЦ. Это обстоятельство делает необходимым решить заодно задачу – какая часть всех молекул данного вещества при данной температуре в среднем может находиться в данной конформации. Взаимосвязь между ПП и конформациями является самостоятельным вопросом, требующим отдельного рассмотрения.

Приведем примеры, подтверждающие необходимость учёта ПП.

1. Из эксперимента известно, что ортозамещенные ароматические соединения (например, производные анилина [2]) реагируют значительно медленнее, чем пара – и метазамещенные. Причину этого Гаммет [3, 4] видел в проявлении орто-заместителями наибольшего стерического препятствия. Нами были рассчитаны ПП для производных бензойной кислоты, анилина и фенола, замещённых в о-, м- и п – положениях заместителями Н, Cl, СН₃.

Как видно из таблицы 1, действительно ортозаместители оказывают большее пространственное препятствие, нежели м- и п – заместители.

2. Расчёт ПП, оказываемых тремя атомами хлора и тремя метильными группами в этиловых эфирах трихлор– и триметилуксусной кислоты, показал, что пространственные затруднения в обоих эфирах проявляются почти в одинаковой степени (разница ПП составляет 0,0003). Следовательно, значительная разница в скоростях щелочного гидролиза этих эфиров (в 10⁸ раз) обусловлена лишь электронным фактором [1, 5].

Таблица 1

ПП оказываемые заместителями в пара-, мета- и

ортоположениях относительно функциональной группы

Соединение	РЦ	Заместители
		Н	СН3		Сℓ
		п-,м-, о-	п-, м-	o-	п-, м-	о-
Н(1) 0,113 0,113 0,122 0,113 0,126 С6Н5СОО(2)Н(1) О(2) 0,117 0,117 0,145 0,117 0,150
Н(1) 0,119 0,119 0,136 0,119 0,142 С6Н5О(2)Н(1) О(2) 0,098 0,098 0,124 0,098 0,128
Н 0,104 0,104 0,118 0,104 0,120 С6Н5ΝН2 Ν 0,068 0,068 0,083 0,068 0,084

В том случае, когда заместители оказывают примерно одинаковое полярное влияние, можно оценить роль пространственного фактора. Так, например, низкая скорость кислотного гидролиза этилового эфира метиленопентил – трет-бутилуксусной кислоты по сравнению с этиловым эфиром муравьиной кислоты (в 10⁵ раз) [5] всецело обусловлена пространственными затруднениями. Вычисленная нами разность ПП в этих соединениях относительно РЦ значительна и равна 0,2.

3. Весьма полезным оказывается расчёт ПП при интерпретации результатов нитрования фенантрена. Из таблицы 2, где приведены экспериментальные и теоретические данные нитрования фенантрена, видно, что малым значениям дьюаровых чисел, вычисленным с учетом лишь электронного фактора, соответствуют большие выходы изомеров [6]. Однако это соответствие нарушается для положения 4, что было объяснено авторами проявлением в этом положении наибольших препятствий. Рассчитанные нами ПП для всех положений фенантрена (таблица 2) подтвердили количественно их предложение. Низкий выход изомера с нитрогруппой в положении 2 можно объяснить, по-видимому, судя по L, превалирующим влиянием электронного фактора.

Можно связать выход продуктов с вычисленными ПП следующим полуэмпирическим выражением: (3), где В – выход продукта реакции, L – энергия локализации для данного положения (можно использовать также индекс свободной валентности или полную электронную заселенность РЦ), W – ПП этому положению, m, n – параметры, значения которых обеспечивают согласие с экспериментом (для фенантрена принимали m = 1, n = 5), K – коэффициент, характеризующий реакцию.

Таблица 2

Значения ПП, дьюаровых чисел, экспериментальных и

расчетных выходов мононитроизомеров фенантрена

Формула	Положе-ние	ПП	Дьюаровые числа или L*	Выход изомеров, %	Выход по формуле (3), един. К
	10 0,1777 1,80 36,1 0,2330 1 0,1777 1,86 26,2 0,2218 2 0,1604 2,18 6,8 0,1937 3 0,1604 2,04 21,8 0,2140 4 0,1984 1,96 5,6 0,1837

* L и дьюаровые числа рассматривались равносильными параметрами.

4. На примере реакции йодистых алкилов с триэтиламином, хинуклидином и пиридином [7] нами была установлена связь ПП с энергией активации и размером алкила. Как видно из таблицы 3, с увеличением алкила ПП и энергия активации симбатно возрастают. Реакция может протекать как по S_N1, так и S_N2 механизмам. Более вероятный механизм реакции определяется лимитирующей стадией отщеплением иона йода.

Таблица 3

Связь ПП с энергией активации и механизмом

взаимодействия йодистых алкилов с триэтиламином

Соединение	ПП		Энергия активации, ккал
	SΝ1	SΝ2
С3Н3J 0,1000 0,1542 9,7000 С2Н5J 0,1219 0,1900 12,5000 Изо-С3Н7J 0,1580 0,2260 16,0000

5. Экспериментально установлено [8], что относительная скорость взаимодействия фенацилхлоридов с ионом йода резко снижается по мере увеличения размера R и R΄ (относительная скорость реакции при R=R΄=Н принято равной 100). Это снижение скорости обусловлено снижением пространственной доступности РЦ (таблица 4).

Первоначальное резкое снижение скорости реакции при переходе от и последующее нивелирование скорости при замене двух атомов водорода метильными группами обусловлено конкуренцией F и B–напряжений. В данном случае F - напряжение превалирует над В-напряжением. Этот пример показывает, что при оценке скорости реакции необходимо количественно учитывать конкуренцию F и В – напряжениями.

Таблица 4

Значение ПП относительная скорость (V)

реакции фенацилхлоридов и ионом йода

Соединение	ПП	V
0,171 100 0,2345 1,3 0,2980 0,29

Определенную роль в уменьшении скорости имеет и электронный фактор, связанный с увеличением их электронодонорности. Это предложение подтверждается значениями электронной плотности на РЦ (рисунок 2), которые были рассчитаны на ЭВМ–М–22 простым методом Хюккеля. За гетероатом Х принят фрагмент .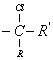

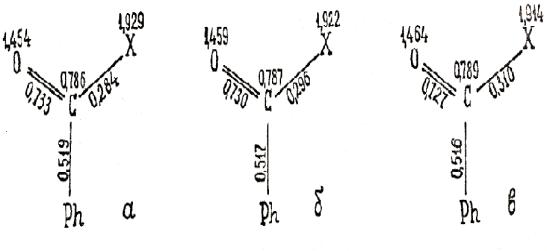
Рисунок 2. Молекулаларные диаграммы молекул фенацилхлоридов:

а) R=R΄=СН₃, a_х = a₀ + 1,75b₀;

б) R=Н, R΄=СН₃, a_х = a₀ + 1,625b₀;

в) R=R΄=Н, a_х = a₀ + 1,5b₀.

6. Одним из примеров, ярко подтверждающих практическую полезность предлагаемой методики расчета ПП, является объяснение факта уменьшения выхода ортозамещенных продуктов монитрования ряда алкилбензолов (толуол, этилбензол, изопропилбензол, третбутилбензол) с увеличением алкила [9]. Лефевром было сделано предположение [9], что решающую роль в этом снижении играет пространственный фактор. Другие объяснили это сильным ортопараориентирующим влиянием метильной группы по сравнению с другими алкильными группами [10]. Расчет ПП, проведенный нами (таблица 5), подтвердил правоту Лефевра. Как видно из таблицы 5, орто-положение в указанных соединениях оказывает значительное стерическое сопротивление. Это приводят к возрастанию вероятности атаки реагентом других положений (пара- и мета-).

Таблица 5

Выход изомеров, образующихся при мононитровании

алкилбензолов, и значения ПП

Соединение	Выход изомеров, %			Литература	ПП
	о-	м-	п-		о-	м-	п-
С6Н5СН3 57 3,2 40 [11] 0,1919 0,1604 0,1604 С6Н5СН3 45 6,5 48 [12, 13] 0,2130 0,1641 0,1659 С6Н5СН(СН3)2 30 7,4 62 [13, 14] 0,2341 0,1677 0,1715 С6Н5С(СН3)3 12 8,5 70 [14] 0,2552 0,1715 0,1770

Обращает на себя внимание несоответствие между значениями ПП, оказываемых мета-положением и экспериментальными выходами мета-изомеров (таблица 5). Таким низким значениям ПП должны соответствовать более высокие выходы продуктов. Объяснение этого противоречия возможно при учёте обоих факторов пространственного и электронного. Как показывают молекулярные диаграммы (рисунок 3) толуола и третбутилбензола, мета-положения заряжены положительно (хотя и незначительно), и вероятность подхода О₂, имеющего в качестве РЦ положительно заряженный атом азота, понижение электростатическим фактором. Тем самым облегчается подход О₂ к орто и пара-положениям, что подтверждается данными распределения p-электронных зарядов в этих соединениях. Однако вклад электронного фактора незначителен: орто- пара-ориентирующее влияние проявляется почти в одинаковой степени в этих соединениях (разница в третьем знаке), тогда как разница в пространственных характеристиках наблюдается во втором знаке, т.е. на порядок выше.

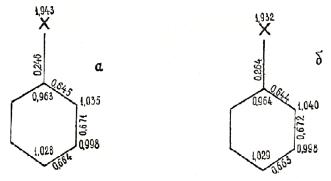
Рисунок 3. Молекулярные диаграмалары толуола и третбутилбензола:

а) Х = СН₃; б) Х = С(СН₃)₃.

7. Авторами работ [15] было обнаружено, что теория граничного электрона, оправдавшая себя на многочисленных примерах, оказалась несостоятельной в случае молекулы 3,4-бензофенантрена. Согласно этой теории наиболее активными положениями в молекуле является 1,12. Однако экспериментальные факты свидетельствуют о наибольшей активности положений 5,8. Такое отклонение от теории было объяснено значительными пространственными затруднениями, проявленными положениями 1,12 по сравнению с 5,8.

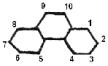
Приведенные в таблице 6 значения ПП, количественно подтверждают это предположение. Положение 1 (12) оказывает наибольшее стереосопротивление атакующему реагенту, а 5 (8) – наименьшее.

Таблица 6

Значение ПП различных положений 3,4–бензофенантрена

Структурная формула	Положение	ПП
	1 (12) 2 (11) 3 (10) 4 (9) 5 (8) 6 (7)	0,2310 0,1664 0,1664 0,1777 0,1377 0,1777

Разобранный пример убедительно показывает, что не всегда можно установить наиболее реакционноспособный центр на основании лишь знаний электроннохимических характеристик молекул, необходимо иметь также количественные данные пространственного фактора.

Таким образом предлагаемая методика расчёта ПП является полезным расширением круга индекса реакционной способности.

ЛИТЕРАТУРА

1. Пространственные эффекты в органической химии / Под ред. Ньюмена М.С.. –М.: ИЛ, 1960. -719 c.

2. Темникова Т.И. Курс теоретических основ органической химии. –М.: Химия, 1968. - 1006 c.

3. Гаммет Л. Основы физической органической химии. Скорости, равновесия и механизмы реакций. –М.: Мир, 1972. - 534 c.

4. Jaffe H.H. / A reexamination of the Hammett eguation // Chem. Phys., 1953. - V. 53, № 2. - P. 191-261.

5. Реутов О.А. Теоретические основы органической химии. М.: МГУ, 1964. - 700 c.

6. Dewar M.J.S. / Molecular Orbital Theory of Organic Gemistry. 1. General Principles // J. Amer.Chem. Soc., 1952. - V. 74, № 13. - P. 3341-3345; ІІ. - Р. 3345-3350.

7. Reeve W., McCaffery E.L., Kaiser T.E. / Relative importanсе of steric and inductive effects in S_N2 displаcement reactions // J. Amer. Chem. Soc., 1954. - V. 76, № 8. - P. 2280-2281.

8.166. Brown H.C., Eldred N.R. / Studies in Sterochemisry. XIV. Reaction of Triethylamine and Quinuclidіne with Alkyl Halides: Steric Effects in Displacement Reactions // J. Amer. Chem. Soc., 1949. - V. 71, № 2. - P. 445-450.

9. Le Fevre R.J.W. / Volume Effects of Alkyl Groups in Aromatiс Compounds. ІІ. Jnfluence of a Group CR₁R₂ Alk Substitution. // J. Chem. Soс., 1933. - P. 980-984; V. The Monosulphonatiоn of p-cymene // 1934. - P. 1501-1502.

10. Ингольд К. Теоретические основы органической химии. –М.: Мир, 1973. - 1056 c.

11. Hollemman A.F., Vermeulen J., de Mooy W.J. / La nitrаtion du toluene et de ses derives chlоres dans la сhaіne laterale // Rec.d.trav. Chim., 1914. - V. 33. - P. 1-34; Jngold C.K., Lapworth A., Rothstein E., Ward D. / Jnflunce of Directung Groups оn Nuclear Reactivity in Oriеnted Aromatic Substitutions. ІІ. Nitrotion of Toluene // J. Chem. Soc., 1931. - P. 1959-1982.

12. Cline E. L., Reid E.E. / Some derivatives of ethylbenzene // J. Amer. Chem. Soc., 1927. - V. 49. - P. 3150-3156; Вrown H.C., Bonner W.H. / Distribution of isomers in the mononitration of ethyl- and isopropylbеnzene. Further evidencе for a steric effect in isomer distribution // J. Amer. Chem. Soc., 1954. –V. 76, № 2. - P. 605-606.

13. Vavon G., Callier A. / Jsomerie cis et trans et empechement sterique. IV (1). Etude des O-isopropylcyclohexanols (2) // Bull. Soc. Chim., France, 1927, V. 41. - P. 357-367.

14. Cohn H., Hyghes E.D., Jones M.H., Peeling M.G. / Effects of Alkyl Groups in Electrophilic Additions and Substitutions // Nature, 1952. - V. 169. - P. 291.

15. Fukui K., Yonezawa T., Shingu H. / A molecular orbital theory of reactivity in aromatic, hydrocarbons // J. Chem. Phys., 1952. -V. 20, № 4. - P. 722-725.